Mathematicians Anonymous (Or Not So Anonymous)
Hello, everyone. I'm Matt, and I'm a mathematician. I've been a mathematician for the last 12 years. The last theorem I proved was today (holds up his Theorem-Proving Chip). 0 is the only number that matters as that is the last day since I've been a mathematician. In fact, all of mathematics can be constructed from nothing. I have a much deeper understanding of creation ex nihilo.
sits back down
Heed My Words!
For those in the academy or considering pursuing a career in the academy after obtaining a bachelor's degree, I would like to offer some meaningful advice.
DON'T DO IT!
Now that you've decided to ignore my suggestion, let me describe some insights that I learned from being a math postdoc. I spent the last 18 months bouncing between 3 different postdocs before completely switching to a new area within IBM Research and doing High Performance Computing, i.e. designing parallel algorithms for scientific applications to be used on large-scale super computers that do the majority of the calculations on Graphical Processing Units (GPUs).
Now I Program These Bad Boys

Postdoc Life
Postdoctoral life is very different from graduate student life, although very much the same. You have much more freedom to choose the research that interests you, beyond a project that your supervisor hands to you. For those who are self-motivated and intellectually curious, this freedom can be highly beneficial. It can also hurt your career if not nurtured properly. The publish or perish paradigm still exists, and you are expected to produce results on your latest scientific inquiries, even if you do not believe the work is significant. All in all, this part of the job is marketing your research as a product. You do not want to say that it was trivial in hindsight (most of the best results are!) nor do you want to expand on 'failed results' (although, I think that knowing what does not work is almost as good or even better than knowing what does work).
I spent anywhere from 40-80 hours a week consumed by mathematics, either by reading papers, thinking about various problems, or investigating various phenomena. This does not include attending conferences and seminars or interacting with other (visiting) scientists at the institutions where I held a visiting position.
Looking back at it now, I should have spent more time networking and writing papers. In fact, I believe this to be the biggest way of landing any job.
Applied Algebraic Geometry
As a mathematician and a scientist, I find (nearly) everything fascinating. You can easily scratch the surface without digging too deeply in most disciplines and research a topic that interests you. The biggest hurdle is researching a known concept and presenting unknown connections to the community at large. Because of the sheer volume of literature that exists, this task can be daunting!
My original area of study (beyond general mathematics) is in Applied Algebraic Geometry, specifically finding all the solutions of a system of nonlinear polynomials using numerical homotopy continuation methods. My expertise (meaning, my dissertation subject, which practically very few other people in the entire world truly understood) was in finding the solutions to polynomial systems with the same monomial structure but with different coefficients and implementing such algorithms in parallel, as well as other algorithmic development specific to certain scientific applications.

I was fortunate enough to spend much of those 18 months studying problems of interest to me, loosely related to applied algebraic geometry, and never particularly caring if the ideas I investigated were of interest to the general community at large.
Now, I allocated a good deal of time learning about techniques, algorithms, and pure mathematics in which I was not as well-versed as my dissertation subject, namely symbolic methods and other, more highly advanced concepts in algebraic geometry. Although this advanced my own personal knowledge of mathematics, much of the subject area was already known, and I did not publish too many papers during my postdoctoral days. Maybe one or two a year (which, in mathematics is quite good!), but apparently not quite good enough!
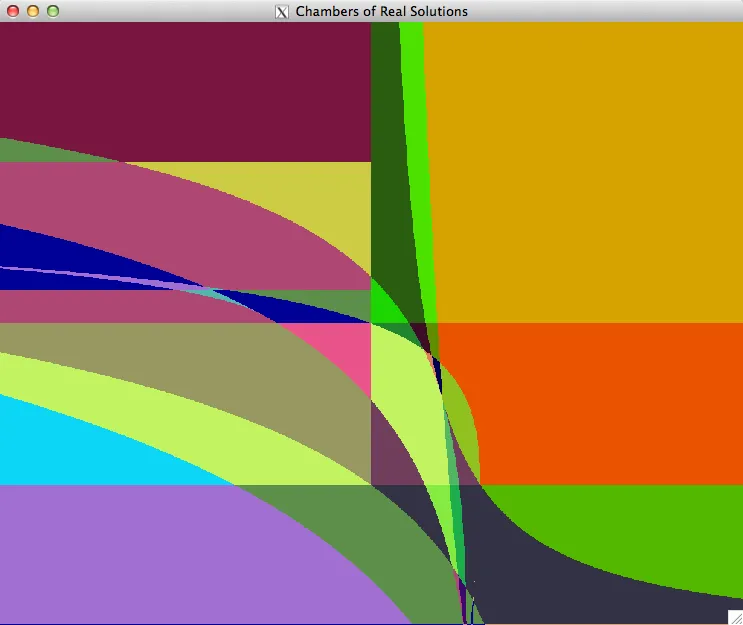
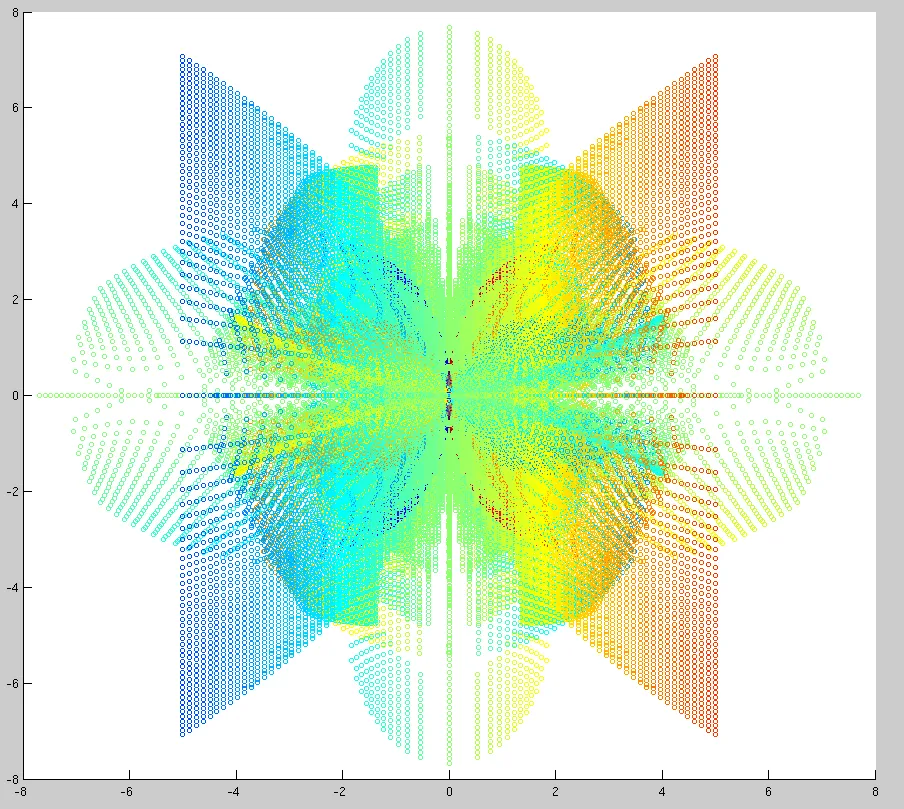
Projections of A-Discriminant Chambers
Discriminants fascinate me! I think they are the bee's knees.

Not quite, I suppose, but they come close.
If you remember the quadratic equation (Ax^2 + Bx + C = 0), the discriminant is B^2 - 4AC and when the discriminant vanishes (i.e. is equal to 0) is precisely when this system has a double root. This concept can be generalized to an arbitrary system of equations in any number of variables. The discriminant of a function F is defined in terms of the (symbolic) coefficients of F. A point on the discriminant variety is then some choice of coefficients that causes a double root or a singularity. Singularity theory is a very difficult subject, especially when you start talking about singularities on quasi-coherent sheafs or on Tangent Bundles or Co-Tangent Bundles or any number of other geometric objects.
The following images are 2 dimensional projections onto the coefficient-parameter space. Each pixel is one point on the coefficient-parameter space in an evenly distributed discretization. Coefficient-parameter points that are the same color have the same number of real solutions. The boundaries between colors are points the discriminant variety. They are places where 2 real solutions 'degenerates' into one. One one side of the boundary, those two solutions are real and on the other, the two solutions are complex.
Points that are places where multiple chambers intersect are even more special in that these have higher multiplicity structure, i.e. multiplicities of order N, multiple pairs of degeneracies, or any combination of these.
These images were created using data (gigabytes!) generated from bertini and paramotopy and visualized with openGL or MatLab.
Steady States of Crystalline Lattice Structures

The Monks' Equations
An Amoeba or Approaching a Tropical Line in the Limit

Achieving Success as a Postdoc
In mathematics (and computer science and all other disciplines), posing well-defined questions is probably the main key to success. The other aspect of good scientific research is in story-telling. And finally, all jokes aside, you want to make your research sound as sexy and cool as possible. As an example, the term "dirty data" still makes me chortle. The dirtier the data the better, some say.
Was Math All I Did?
Well, not quite. I organized a hike outside of Daejeon in Korea, visited Seoul (hit a triple Bull's Eye at a bar near the college campus, don't ask me to repeat it, as I don't think I'd ever be able to), tore my knees in the foothills on the backside of Berkeley, saw a Midsummer's Night Dream, managed to see parts of China with my fiancee (@edgeland), explored portions of Toronto and even visited Montreal.
Needless to say, I had lots of fun and learned way more math than I would ever have imagined.
Much of the world sees value in the relationships and networks that you foster with people. Academia is no different, and social outings play an important role in making you more personable.
Looking Over Berkeley and the Bay


Continual Life as a Postdoc
Unfortunately, I did not obtain an academic position (I was aiming for an R1) but landed an industry postdoc job with IBM instead. I'm not complaining. It's challenging research and definitely cutting edge and bears a completely different mentality than life in academia. I have more 'hands-on' experience with scientific applications than I would have before and can bring the insight of my mathematical background and algorithmic development expertise to scientists at Oak Ridge National Laboratory.
What's Next?
What will I do after this postdoc? I'm not sure. I want to say no more postdocs, but nothing is ever certain.
But I do like applications of distributed ledger technologies.