En este post queremos deducir la técnica para derivar la suma o diferencia de funciones. Pero, en plan de simplificar la explicación trataremos solo la suma lo cual es equivalente para la diferencia.
Esto es:
Dadas dos funciones diferenciables g(x) y h(x), con dominio en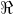 
(conjunto de los números reales), se quiere determinar la derivada de f(x)=g(x)+h(x)
Deduciremos esta técnica aplicando la definición de derivada
Sabemos que:
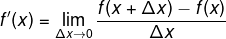
Y que además
Entonces:
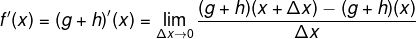
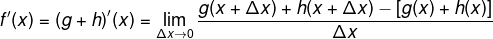
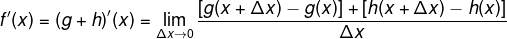
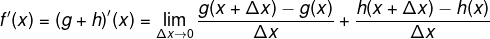
Entonces concluimos la siguiente proposición:
Si f(x)=g(x)+h(x) entonces f´(x)= g'(x)+h'(x)
Veamos algunos ejemplos:
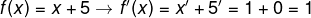
Comentarios:
El ejemplo anterior muestra que la función f es la suma de la función identidad más la función constante, en tal sentido, para obtener su derivada aplicamos la técnica anteriormente deducida, como en efecto así se hizo.
Pero, también puede ser considerada una función afín cuya derivada se identifica con la pendiente de la recta, en este caso la derivada es 1 (lo cual coincide con el resultado anterior).
Veamos otro ejemplo de este caso:
Si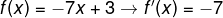 
Este resultado puede ser verificado usando la derivada de una suma de funciones donde g(x)=-7x y g(x)=3
Consideremos este ejemplo donde vemos varias sumas y diferencias de funciones potencia, afín y constante.
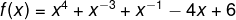
Aplicando la técnica deducida, nos queda así:
 |
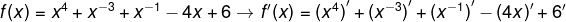
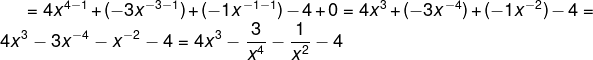Déjame algún comentario si tienes alguna duda
▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄▄▲▄
Créditos
Usamos el Editor de Ecuaciones LaTeX para editar las ecuaciones.
El contenido es totalmente original.