In Book 1 of Euclid’s Elements, Postulate 4 reads (Fitzpatrick 7):
| Greek | English |
|---|---|
| δʹ. Καὶ πάσας τὰς ὀρθὰς γωνίας ἴσας ἀλλήλαις εἶναι. | 4. And that all right-angles are equal to one another. |
As we saw in a previous article, the verb Ἠιτήσθω [Ēitēsthō], Let it have been postulated, is understood to apply to all five postulates. At least one manuscript omits the word ἀλλήλαις [allēlais], to one another (Heiberg 8). The inclusion of this word makes it clear that for Euclid equality (or congruence) was a relation between geometric objects (Liddell & Scott 65). He is not saying that all right angles are equal to some standard unit of angular measurement. The right angle is the standard unit of angular measurement.
Euclid defined the right angle in Definition 10:
And when a straight-line stood upon (another) straight-line makes adjacent angles (which are) equal to one another, each of the equal angles is a right-angle, and the former straight-line is called a perpendicular to that upon which it stands. (Fitzpatrick 6)
In other words, when a perpendicular stands upon another line, the two angles at the foot of the perpendicular are equal to each other by definition. This is the property that makes the first line a perpendicular to the other line. Postulate 4 states that the right-angles formed when any perpendicular stands upon any line are equal to all other right-angles. Consider for example the following diagram, in which the line CD is perpendicular to the line AB, and the line GH is perpendicular to the line EF:
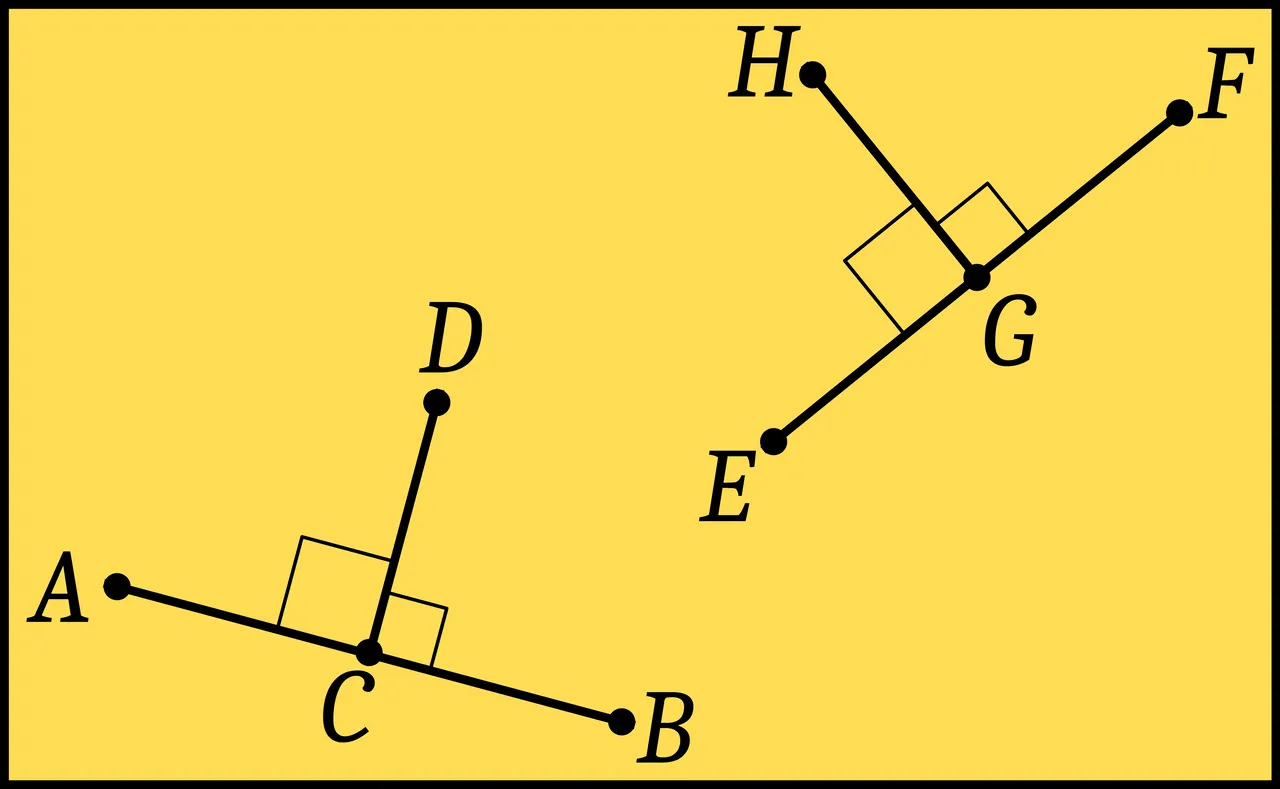
Definition 10 tells us that: AĈD = BĈD and EĜH = FĜH.
Postulate 4 tells us that: AĈD = BĈD = EĜH = FĜH.
Is Postulate 4 Redundant?
On the face of it, Postulate 4 sounds like a tautology: All right angles are right angles. It is actually omitted from some manuscripts (Peyrard 454), and in some editions it is included among the Common Notions (Heiberg 9, August 311). What purpose does this postulate serve in the Elements?
... why the heck do we need a postulate that says that all right angles are equal to one another? You probably remember learning in a middle or high school geometry class that right angles are 90 degree angles, and two angles are congruent if they have the same degree measure. We don’t need a whole postulate that says this. It’s just part of the way we define angles. Why not a postulate that says that all 45 degree angles are equal to one another? Or all 12 degree angles? The fourth postulate seems a bit bizarre. But Euclid knew what he was doing, so there must be a reason for this postulate. (Lamb)
Today, we generally measure angles in degrees or radians, but for Euclid the fundamental unit of angle mensuration was the right angle. For example, in Proposition 1:32 Euclid proves that the sum of the three interior angles of a triangle is equal to two right angles. As David Joyce points out:
This postulate forms the basis of angle measurement. The only angle measurement that occurs in the Elements is in terms of right angles. (Joyce)
It is precisely because Euclid used the right-angle as the unit for measuring all angles that he needs Postulate 4. But there is more to it than that. In Proposition 1:4, the so-called Side-Angle-Side Theorem, Euclid proves that if two sides of a given triangle are equal in length respectively to the corresponding sides of another triangle and if the angles between the two sides are also equal, then the two triangles are congruent—ie equal in all respects.

His proof involves applying one triangle to the other—ie superimposing it upon the other. In modern terms, we would say that one triangle has been translated and rotated (and, possibly, reflected in a line) so that it is mapped onto the other triangle. Some geometricians have argued that the validity of applying one figure to another in this manner ought to have been included as another postulate, as Euclid never proves its validity. For example, Richard Fitzpatrick adds the following footnote to his translation of the relevant sentence in Proposition 1:4:
The application of one figure to another should be counted as an additional postulate. (Fitzpatrick 11 fn)
It might be argued that Euclid did include this—but as a Common Notion rather than as a Postulate. The fourth of his Common Notions reads:
And things coinciding with one another are equal to one another. (Fitzpatrick 7)
But, as Lamb points out, this is not sufficient. We must postulate that when one right angle is applied to another right angle, the former will indeed coincide with the latter:
Now it makes a little more sense that Euclid would want a postulate that states that right angles are congruent. We need to know that creating a pair of right angles on one piece of paper is the same as creating them on another piece of paper. We need to be able to put the pieces of paper on top of each other and have the angles line up exactly. In effect, the fourth postulate establishes the right angle as a unit of measurement for all angles. (Lamb)

But this is still not sufficient. It is also necessary to postulate that geometric figures are rigid and invariable under the operations of translation and rotation (and reflection in a line). In other words, when you apply one figure to another, only the location and orientation of the first figure changes. As I learned it in school: translations, rotations, and reflections are isometries : they conserve length, area and measure of angle. Thomas Heath argued that Postulate 4 implies this invariability of figures under such transformations:
While this Postulate asserts the essential truth that a right angle is a determinate magnitude so that it really serves as an invariable standard by which other (acute and obtuse) angles may be measured, much more than this is implied, as will easily be seen from the following consideration. If the statement is to be proved, it can only be proved by the method of applying one pair of right angles to another and so arguing their equality. But this method would not be valid unless on the assumption of the invariability of figures, which would therefore have to be asserted as an antecedent postulate. Euclid preferred to assert as a postulate, directly, the fact that all right angles are equal; and hence his postulate must be taken as equivalent to the principle of invariability of figures or its equivalent, the homogeneity of space. (Heath 200)
It might be contested that, taken together, Euclid’s Fourth Common Notion and Fourth Postulate only allow us to conclude that when a figure is translated, rotated, and/or reflected, its angles remain unchanged. Do they also authorize us to conclude that the lengths of the sides remain unchanged? A triangle, for example, could be mapped onto another triangle that is similar to the first (ie has the same angles as it has) but is larger or smaller than it.

In Proposition 1:4 Euclid assumes that the side-lengths of a triangle remain unchanged when the triangle is applied to another triangle. This is understandable, as Euclid probably did not envisage actually moving the triangle. For Euclid, the triangle is an idea, not a set of marks on a piece of paper. Much ink has been spilled on Euclid’s method of applying one figure to another, but we will postpone further discussion of this controversy until we come to study Proposition 1:4.
Thomas Heath also argued that Postulate 4 is a prerequisite of Postulate 5:
As to the raison d’être and the place of Post. 4 one thing is quite certain. It was essential from Euclid’s point of view that it should come before Post. 5, since the condition in the latter that a certain pair of angles are together less than two right angles would be useless unless it were first made clear that right angles are angles of determinate and invariable magnitude. (Heath 201)
Can Postulate 4 Be Proved
In his Foundations of Geometry, the German mathematician David Hilbert argued that Euclid’s Postulate 4 ought to be a proposition—ie theorem:
By aid of theorems 12 and 13, it is possible to deduce the following simple theorem, which Euclid held—although it seems to me wrongly—to be an axiom.
Theorem 15. All right angles are congruent to one another. (Hilbert 20)

Hilbert proceeds to prove Euclid’s Fourth Postulate as his Theorem 15 (Hilbert 20-21). In contrast to Euclid’s approach to the subject, Hilbert’s geometry was rigorously axiomatic. This rigor required no less than twenty-one axioms, or postulates. (There were actually twenty-two axioms in the first edition of Grundlagen der Geometrie, but one of these was later shown to be redundant.) It could be argued that the Fourth Postulate cannot be proved if we only have the four remaining Postulates and the five Common Notions as axioms. But if this were the case, why did Hilbert state explicitly that Euclid was wrong to include this as a postulate?
The key question is: Can Postulate 4 be proved using only the other Postulates and the Common Notions as axioms? In other words: Is the Fourth Postulate independent of the other Postulates and the Common Notions?
The answer to this question is, I believe, no. Hilbert’s proof of his Theorem 15 depends ultimately on four of his so-called Axioms of Congruence: IV:3, IV:4, IV:5, and IV:6:
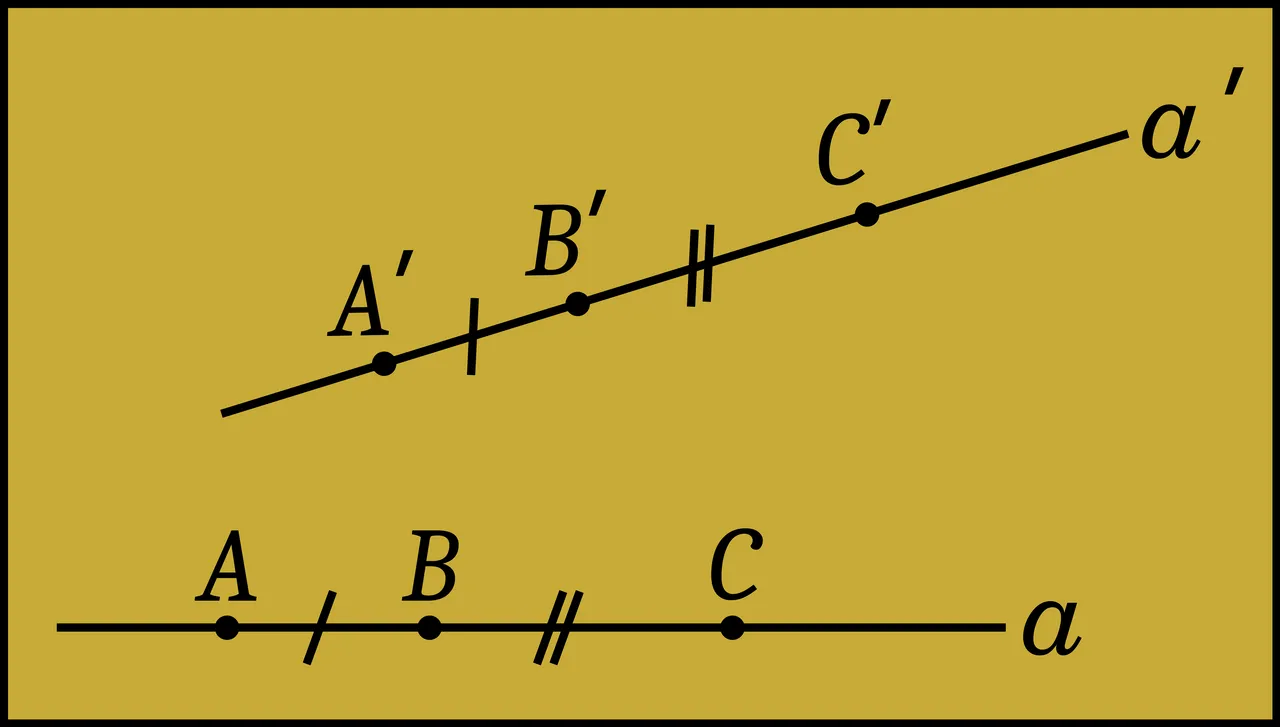
- IV:3 Let AB and BC be two segments of a line a which have no points in common aside from the point B, and, furthermore, let A′B′ and B′C′ be two segments of the same or of another line a′ having, likewise, no point other than B′ in common. Then, if AB ≡ A′B′ and BC ≡ B′C′, we have AC ≡ A′C′.
This follows from Euclid’s Common Notion 2: If equal things are added to equal things then the wholes are equal.
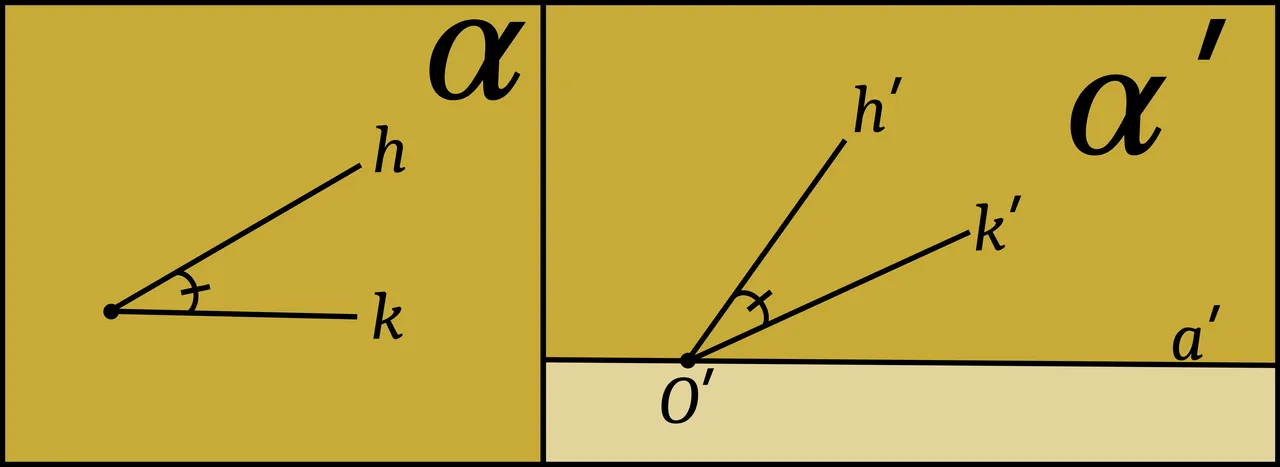
- IV:4 Let an angle∠(h,k) be given in the plane α and let a line a′ be given in a plane α′. Suppose also that, in the plane α′, a definite side of the straight line a′ be assigned. Denote by h′ a ray of the straight line a′ emanating from a point O′ of this line. Then in the plane α′ there is one and only one ray k′ such that the angle∠(h, k), or∠(k, h), is congruent to the angle∠(h′, k′) and at the same time all interior points of the angle∠(h′, k′) lie upon the given side of a′. We express this relation by means of the notation∠(h, k) ≡ ∠(h′, k′).
This partly follows from Euclid’s Proposition 1:23, a construction that allows one to create at a given point on a given line an angle congruent to a given angle, and from Proposition 11:31, in which the constructed congruent angle is in a different plane to the given angle. But the part that states that all interior points of the angle∠(h′, k′) lie upon the given side of a′ is never proved or postulated by Euclid. In a footnote to Proposition 1:16, upon which 1:23 depends, Richard Fitzpatrick notes:
The implicit assumption that the point F lies in the interior of the angle ABC should be counted as an additional postulate. (Fitzpatrick 21)
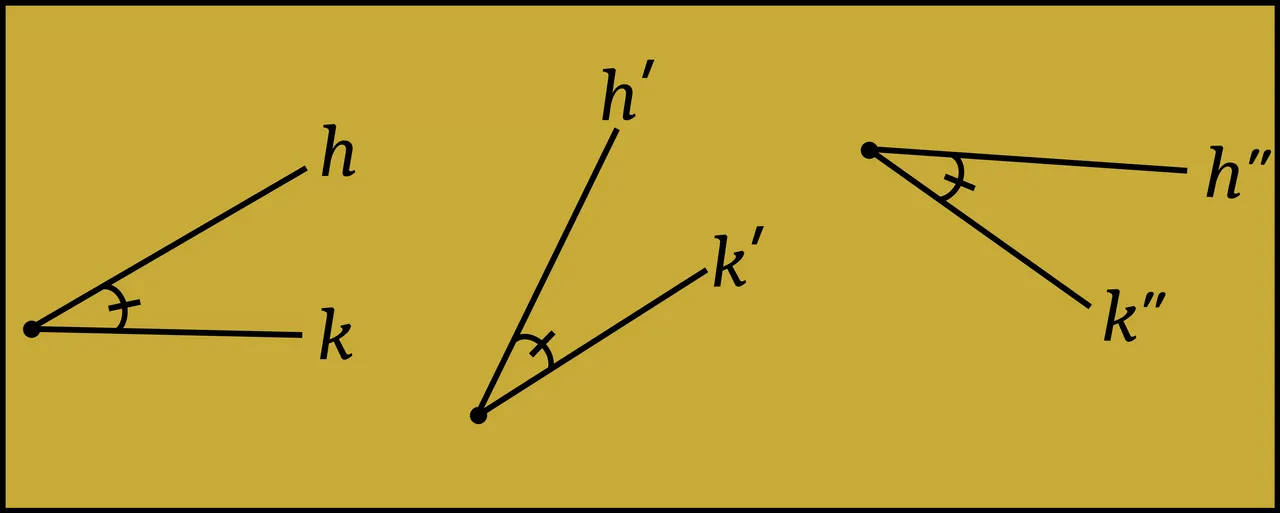
- IV:5 If the angle∠(h, k) is congruent to the angle∠(h′, k′) and to the angle∠(h″, k″), then the angle∠(h′, k′) is congruent to the angle∠(h″, k″); that is to say, if∠(h, k) ≡ ∠(h′, k′) and∠(h, k) ≡ ∠(h″, k″), then∠(h′, k′) ≡ ∠(h″, k″).
This follows from Euclid’s Common Notion 1:
Things equal to the same thing are also equal to one another. (Fitzpatrick 7)
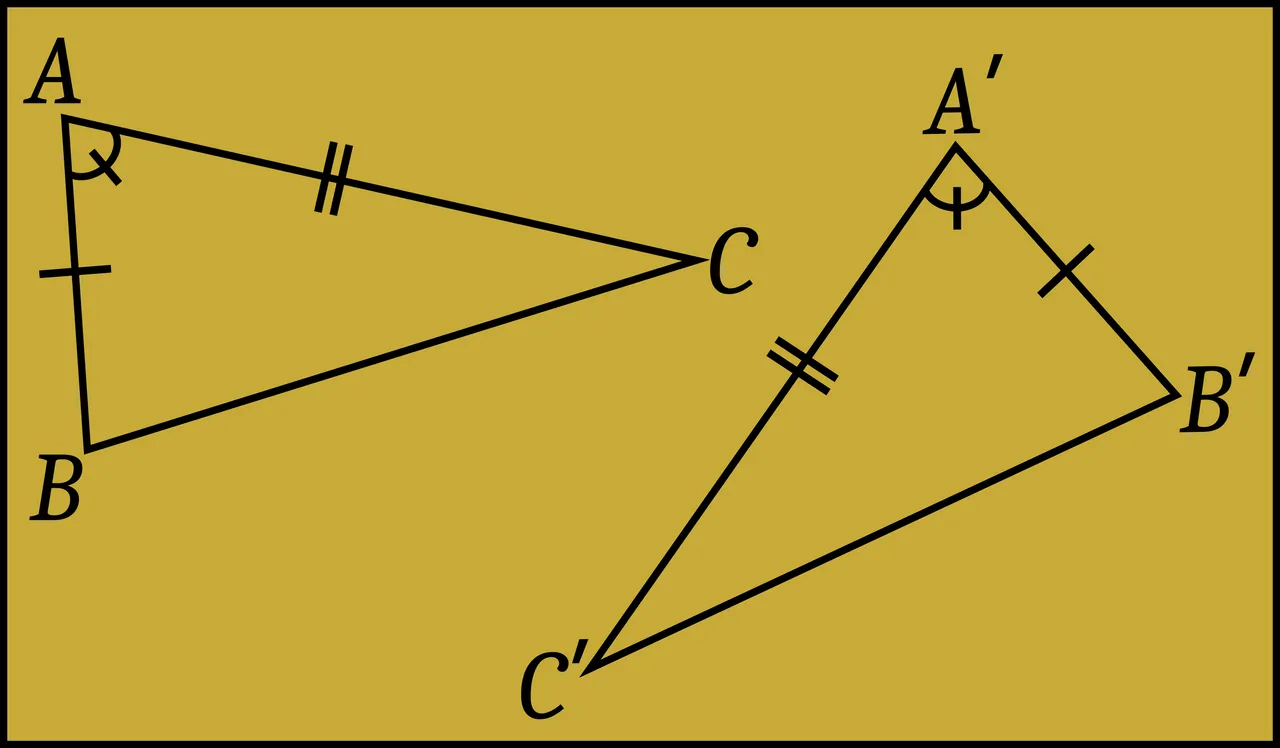
- IV:6 If in the two triangles ABC and A′B′C′ the congruences AB ≡ A′B′, AC ≡ A′C′, ∠BAC ≡∠B′A′C′ hold, then the congruence∠ABC ≡∠A′B′C′ holds (and, by a change of notation, it follows that∠ACB ≡∠A′C′B′ also holds).
This follows from Euclid’s Proposition 1:4, the familiar Side-Angle-Side Theorem (Fitzpatrick 10-11). Remember that this Proposition uses Euclid’s method of applying one figure to another, which Heath believes requires Postulate 4.
In conclusion, Postulate 4 cannot be proved using only the remaining Postulates and the Common Notions as axioms. We require at least one more axiom to take care of the second part of Hilbert's Axiom IV:4. And if Heath is correct, we require Postulate 4 itself to prove Proposition 1:4, which is in turn required to prove Postulate 4. We will be arguing in a circle (ie begging the question) if we use Postulate 4 as part of the proof of Postulate 4.
Not all professional mathematicians agree that Postulate 4 cannot be proved without adding extra axioms to Euclid’s Postulates and Common Notions. For example:
Many scientists dealing with the Elements tried to reduce the number of axioms. The attempt to introduce minimum number of axioms on which geometry could be developed continued. In this regard Euclid’s fourth postulate dealing with the equality of right angles was found to be superfluous. Like many other propositions, this can be rigorously proved. (Adhikary 3)
Attempts to Prove Postulate 4
Nevertheless, several of Euclid’s successors have presented alleged proofs of Postulate 4. One of the earliest was that of Proclus, who flourished in the 5th century, though he did not claim to be the first. Proclus actually believed that the equality of right angles was obvious from our common notions, given the definition of the right angles, and therefore did not require a proof. Nevertheless, he offered the following “proof”:
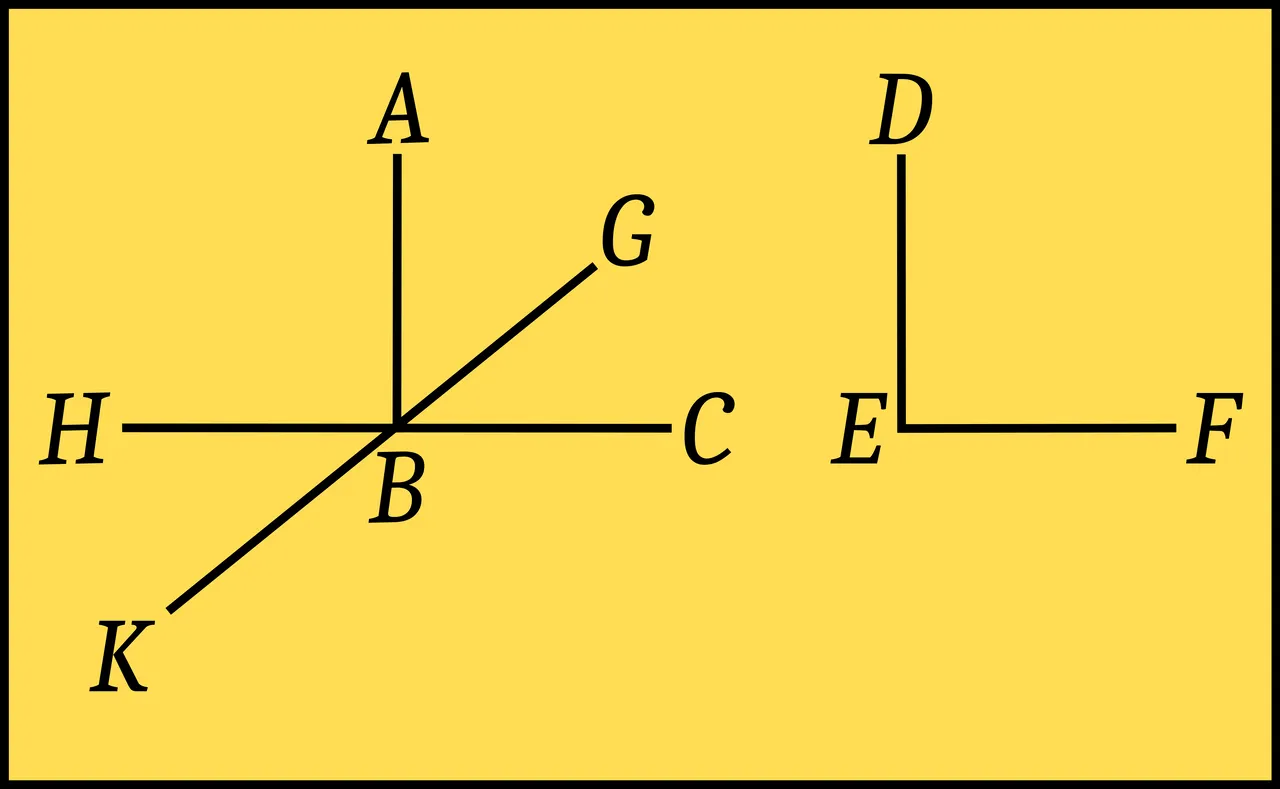
But if we must provide a graphic proof of this postulate, let us assume two right angles, ABC and DEF. I say they are equal. If they are not, one of them will be greater than the other. Let this be the angle at B. Then if DE be made to coincide with AB’ the line EF will fall within the angle [ABC], say, at BG. Let BC be extended to H. Since ABC is a right angle, so also is ABH, and the two angles are equal to one another (for a right angle is by definition equal to its adjacent angle). Angle ABH, then, is greater than angle ABG. Now let BG be extended to K. Since ABG is a right angle, its adjacent angle also will be a right angle, equal to ABG. The angle ABK, then, is equal to angle ABG, so that angle ABH is less than ABG. But it is also greater, which is impossible. Hence it is false that a right angle can be greater than a right angle.
This proof has been given by other commentators and required no great study. (Morrow 147-148, emphasis added)
This proof, or a very similar one, was also advanced by two Persian mathematicians in the Middle Ages:
Al-Nayrizi, a Persian mathematician who flourished in the late 9th and early 10th centuries. His proof of Postulate 4 can be found in his Commentary on Euclid’s Elements of Geometry Books 1-4, which was translated into Latin in the 12th century by Gerard of Cremona.
Abu Sahl al-Quhi, a Persian mathematician who flourished in the second half of the 10th century. Among the many treatises he wrote on the first three books of Euclid’s Elements is his revision of Book 1. This work opens with Al-Quhi’s proof of Postulate 4. His proof is virtually identical to that of Proclus (Berggren & Van Brummelen 430).
As Thomas Heath has shown, however, Proclus’s proof is defective:
A defect in this proof is the assumption that CB, GB can each be produced only in one way, and that BK falls outside the angle ABH. (Heath 100)
In the 18th century, the Italian mathematician Giovanni Girolamo Saccheri devised a more careful proof of Postulate 4, but like Hilbert after him, he included additional premises to close the loopholes in Proclus’s proof (Heath 100-101, Halsted 201-205). Saccheri’s last work Euclides ab omni naevo vindicatus [Euclid Freed from Every Flaw] was first published in 1733 but its significance was only realized after the work was rediscovered by a happy accident in 1889 (Halsted vii).
And that’s a good place to stop.
References
- Pushpa Raj Adhikary, Foundations of Geometry - I, Kathmandu University Journal of Science, Engineering and Technology, Volume 1, Number 1, Kathmandu University, Kathmandu (2005)
- Ernst Ferdinand August, Euclidis Elementa, Part 1, Theodor Trautwein, Berlin (1826)
- J L Berggren & Glen Van Brummelen, Al-Kūhī’s Revision of Book I of Euclid’s Elements, Historia Mathematica, Volume 32, Issue 4, Pages 426-452, Elsevier, Amsterdam (2005)
- Henry Billingsley (translator), The Elements of Geometrie of the Most Auncient Philosopher Evclide of Megara, John Day, London (1582)
- Richard Fitzpatrick (translator), Euclid’s Elements of Geometry, University of Texas at Austin, Austin, TX (2008)
- George Bruce Halsted (editor & translator), Girolamo Saccheri’s Euclides Vindicatus, The Open Court Publishing Company, Chicago (1920)
- Thomas Little Heath (translator & editor), The Thirteen Books of Euclid’s Elements, Second Edition, Dover Publications, New York (1956)
- Johan Ludvig Heiberg, Heinrich Menge, Euclidis Elementa edidit et Latine interpretatus est I. L. Heiberg, Volumes 1-5, B G Teubner Verlag, Leipzig (1883-1888)
- David Hilbert, E J Townsend (translator), Foundations of Geometry, Second Edition, The Open Court Publishing Company, Chicago (1910)
- Henry George Liddell, Robert Scott, A Greek-English Lexicon, Eighth Edition, American Book Company, New York (1901)
- Anthony Lo Bello (editor), Gerard of Cremona’s Translation of the Commentary of Al-Nayrizi on Book 1 of Euclid’s Elements of Geometry, Brill Academic Publishers, Leiden (2003)
- Glenn Raymond Morrow (translator), Proclus: A Commentary on the First Book of Euclid’s Elements, Princeton University Press, Princeton, NJ (1970)
- François Peyrard, Les Œuvres d’Euclide, en Grec, en Latin et en Français, Volumes 1-3, Charles-Frobert Patris, Paris (1814, 1816, 1818)
- Thomas Taylor, The Philosophical and Mathematical Commentaries of Proclus on the First Book of Euclid’s Elements, Volume 1, Volume 2, London (1792)
Image Credits
- Evelyn Lamb: © Quantamagazine, Fair Use
- David Hilbert, Postcard, University of Göttingen, Public Domain
Online Resources
- Evelyn Lamb on Euclid’s Fourth Postulate
- Euclid’s Elements by David E Joyce
- Life of Euclid
- Reading Euclid
