
In this post I thought I would share with you an algebra activity that works really well. I tend to use it at the start of an algebra unit, and it's probably a task best suited to students who have never actually experienced algebra before. So, for us in Australia, generally, the first time a student is introduced to algebra is in Year 7, so I'll make use of this task at that year level, at the commencement of out algebra and equations unit.
Some Task Specifics
| Criteria | Description | |
|---|---|---|
| Purpose | To teach basic algebra (like terms and substitution) | |
| Time required | About 40 to 50 minutes | |
| Year level | Seven, but possibly six and/or eight would benefit | |
| Materials required | Handout, individual wrapped lollies (about 100) |
Introduction
As well as the learning of basic algebraic premises, students get the chance to employ strategy as they try to determine the best colours of lollies to keep and swap as they aim to be the 'richest' group at the end of the task.
At the outset of an algebra unit, I find this activity a fun and engaging way in which to introduce some of the more basic algebraic terms snd operations, specifically, substitution and collecting like terms. I have always used lollies that are wrapped due to the handling that occurs during the activity, but it is probably more important, now than ever, that you only use wrapped lollies (you might even want to provide disposable gloves at the moment too).
Before I step you through how a lesson using this activity looks, if you would like to get the task sheet, this link will take you to it. You should then be able to follow this general approach to the lesson.
Before The Lesson Begins:
- Write (or display electronically) on the board, the variables you are going to assign each lolly colour. I tend to work with lollies that have five different colours, so I assign them variables based upon their wrapper colour. You may need to alter the task sheet to fit in with your arrangements, but that's fine:
- Pink = p
- Yellow = y
- Orange = o
- Red = r
- Purple = e (because p is already taken)
- Assign each variable a monetary value (but keep this a secret for now). This will be substituted at the end of the rounds. A suggested value system could be:
- p = 5c
- y = 10c
- o = 20c
- r = 50c
- e = $1
Initial Setup
Because I use this as an introductory activity to an algebra unit, I will usually spend some time introducing the unit as a whole before introducing the activity.
Once the introduction has been completed, I divide the class into pairs (I usually just assign pairs based upon whom they are sitting next to). You could try the activity on a solo basis, but I find pairs work the best. This way students can support each other as they work through the activity - remember, I generally use this as a unit opener.
Next I hand out the lollies, with strict instructions that students are not to eat them at this point. (You'd be surprised - actually, you probably wouldn't! - at how many will try and tuck in immediately.) Give them an equal number of lollies (e.g. 10 per group), but don't worry if they have uneven colour distribution. This makes the challenge of ending up with the highest value more enthralling.
Give students time to divide the lollies up by colour, and write their first expression. As an example, if you were giving out, say, fifteen lollies to each group, and 'Group A' got 5 reds, 3 oranges, 3 yellows, 3 purples and one pink, their initial expression would look like the following:
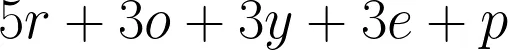
- Have students record their initial expression in the space provided on the third page of the handout (second column). Each row of the table represents one round.
Gameplay
Now that you have students set up with their lollies and their first expression, it is time to play the first round. One round involves each group selecting a certain number of lollies (as stipulated by the teacher) and passing that onto the next group (again, direction to pass is determined by the teacher). So, in one round each group will pass and receive the same amount of lollies.
- Students select the required amount of lollies to pass. Colour selection is up to them.
- Groups pass lollies in the predetermined direction.
- Groups receive the lollies from the previous group. Each group should end up with the same number of lollies they had at the start of the round. For example, if 'Group A' started the round with 15 lollies, and they were instructed to pass three lollies, then they should have received three back resulting in a total of 15 lollies at the end of the passing stage of the round.
- The third and fourth columns on the table are where the groups can record the number and colour of lollies they passed on. If 'Group A' passed 3 yellow, then in the third column, they should record this:
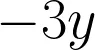
- If 'Group A' received 1 orange and 2 purple, then in the fourth column, they will record the following:
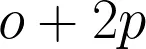
- To conclude the round, groups should work out their new expression based upon the lollies they sent and received in that round. So, to continue watching 'Group A', After round 1, they would now be holding the following 15 lollies: 5 red, 4 orange, 5 purple and one pink, so their expression that would be written in the fifth column would be:
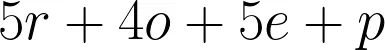
Groups can check that they still have 15 lollies and that their expression reflects this before you commence the next round.
Once satisfied that the correct number of lollies have been sent and received, and that groups have recorded their expressions correctly, the 'end-of-round-expression' can be carried to row two, ready for the next round.
Gameplay continues in this manner for as many rounds as you think are necessary. I usually run it for about five rounds, depending on how I feel groups are picking up the concepts.
Ending The Game
- After you have completed the specified number of rounds, it is time to give your students a quick lesson on substitution. I tend to identify the variables that they have been working with and give a brief explanation of what a variable is and how it can be replaced with a value.
- Display the values that you previously assigned the variables and give another quick example of how students can substitute the values in for their variables to determine the overall value of the lollies they have at the end of the game.
Say 'Group A', after five rounds, ended up with 2 red, 7 orange, 3 pink and 3 purple, they could perform the following substitution to determine the value of the lollies they have:
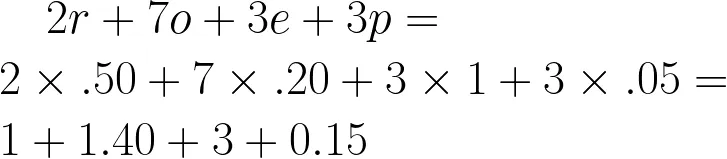
- In this example, 'Group A' would have a total monetary value of $5.55 worth of lollies in their possession.
Then, of course, the group with the highest value of lollies in their possession can get a prize of some sort. Plus, all groups can eat their lollies at an appropriate time. (Unless you want to be a jerk and collect them all back at the end of the lesson!)
Conclusion
I really hope that you have found this a useful lesson idea. If there is anything that you're not able to understand as a result of my possible disarticulation, or some other factor, please leave a comment below and I'll get back to you as soon as I can.
If you just have a general comment, or happen to use this, again, please let me know. Especially if you make use of this. I'd love to hear how you went with it.
Thanks for reading.
Title Image Background//John Moeses Bauan
All other images made using LaTeX Online