~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

08-07-2025 - Mathematical Analysis - Continuous Functions [EN]-[IT]
With this post I would like to give a brief instruction about the topic mentioned in the subject
(code notes: X-77)
Continuous Functions
image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
A function is defined as continuous if a function f at a point x0, making the input values around x0 vary little, the output varies little.
We can say that following this variation the graph of a continuous function does not present jumps or holes.
Here is a list of continuous functions:

Properties of continuous functions and theorems
Sum, product, quotient
The sum, product and quotient of continuous functions remain continuous.
Bolzano's Theorem
Bolzano's theorem is also called the zero theorem and states the following:
Let a function f(x) be continuous in an interval [a.b], if f(a) and f(b) are different from zero and have different signs, then there exists an x0 that belongs to [a,b] such that f(x0) = 0
We can also describe it like this:
let..
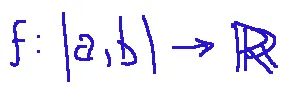
... continuous on the closed interval [a,b].
If the values at the ends have opposite signs, that is...
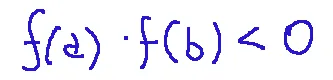
Then there exists at least one point...
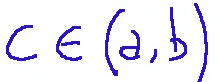
...such that...
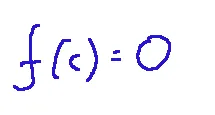
In short, we can say that Bolzano's theorem or zero theorem says that a continuous fiction that starts positive and ends negative, or the opposite, must cancel at least once within the interval.
Below is a graph of a continuous function showing Bolzano's theorem
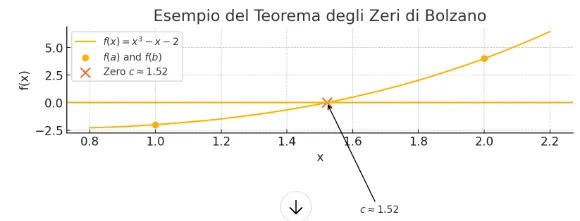
image created with artificial intelligence, the software used is ChatGPT
Continuity theorem of the inverse function
This theorem is very clear and says the following.
We think we have the function...
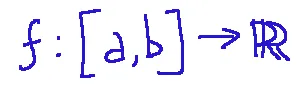
...a continuous and strictly monotonic function, with
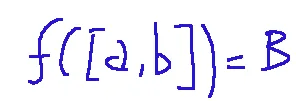
Then the function inverse...
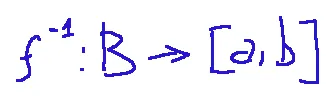
... is continuous
Below is a graph of a continuous monotone function and its continuous inverse.
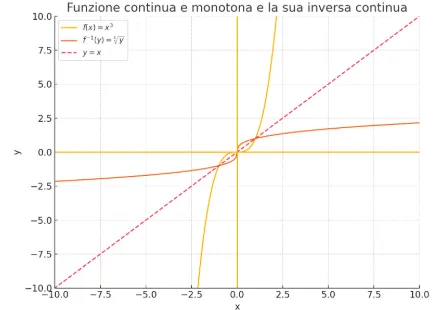
image created with artificial intelligence, the software used is ChatGPT
Example of a function that cancels itself
Let's take the following function as an example:
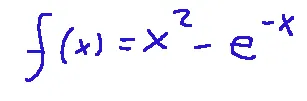
Below is his graph
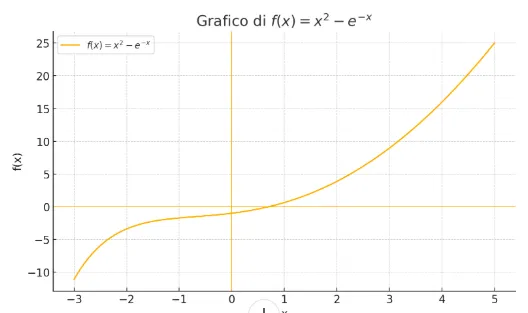
image created with artificial intelligence, the software used is ChatGPT
The orange curve shows the trend of the function.
In this case we see that it cancels out for at least one value between 0 and 1.
Conclusions
When we are faced with a continuous function it means that we are faced with mathematical models that reflect gradual transitions. With continuous functions we are able to calculate speed and probability
Question
The theorem of zeros was conceived by Bernard Bolzano (1781-1848). Did you know that he was a great Bohemian mathematician and philosopher? Did you know that his proof was innovative for the time, because he built his proof on functions, without resorting to geometric figures.
THE END

ITALIAN

08-07-2025 - Analisi Matematica - Funzioni continue [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-77)
Funzioni continue

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Un funzione viene definita continua se una funzione f in un punto x0, facendo variare poco i valori di ingresso attorno a x0, l'uscita varia di poco.
Possiamo dire che a seguito di questa variazione il grafico di una funzione continua non presenta salti o buchi.
Qui di seguito un elenco di funzioni continue:

Proprietà delle funzioni continue e teoremi
Somma, prodotto, quoziente
La somma, il prodotto ed il quoziente di funzioni continue, restano continue.
Teorema di Bolzano
Il teorema di Bolzano è detto anche teorema degli zeri e afferma quanto segue:
Sia data una funzione f(x) continua in un intervallo [a.b], se f(a) e f(b) sono diversi da zero e di segno discorde, allora esiste un x0 che appartiene a [a,b] tale che f(x0) = 0
Possiamo descriverlo anche così:
sia..
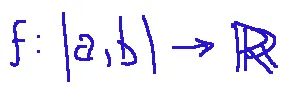
... continua sull'intervallo chiuso [a,b].
Se i valori ai capi hanno segno opposto, cioè...
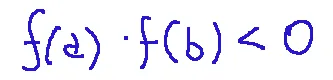
Allora esiste almeno un punto...
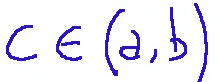
...tale che...
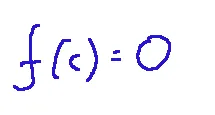
In maniera breve possiamo dire che il teorema di Bolzano o teorema degli zeri dice che una finzione continua che parte positiva e finisce negativa, oppure il contrario, deve annullarsi almeno una volta dentro l'intervallo.
Qui di seguito un grafico di una funzione continua in cui è mostrato il teorema di Bolzano

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Teorema della continuità della funzione inversa
Questo teorema è molto chiaro e dice quanto segue.
Pensiamo di avere la funzione...
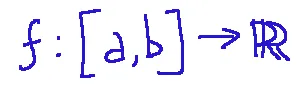
...una funzione continua e strettamente monotona, con
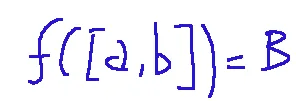
Allora la funzione inversa...
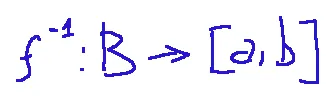
... è continua
Qui di seguito un grafico di una funzione continua e monotona e la sua inversa continua.

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
Esempio di una funzione che si annulla
Prendiamo come esempio la funzione seguente:
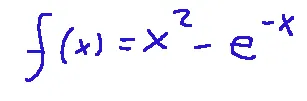
Qui di seguito il suo grafico

immagine creata con l’intelligenza artificiale, il software usato è ChatGPT
La curva di colore arancione mostra l'andamento della funzione.
In questo caso vediamo che si annulla per almeno un valore compreso tra 0 e 1.
Conclusioni
Quando siamo davanti ad una funzione continua vuol dire che siamo davanti a modelli matematici che riflettono transizioni graduali. Con le funzioni continue siamo in grado di calcolare velocità e probabilità
Domanda
Il teorema degli zeri, fu ideato da Bernard Bolzano (1781-1848). Lo sapevate che egli fu un grande matematico e filosofo boemo? Lo sapevate che la sua dimostrazione fu innovativa per il tempo, perché costruì la sua dimostrazione sulle funzioni, senza ricorrere a figure geometriche.
THE END