
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

11-07-2025 - Mathematical Analysis - Integrals of rational functions [EN]-[IT]
With this post I would like to give a short instruction about the topic mentioned in the subject
(code notes: X-60-59)
Integrals of rational functions
image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
Let's start with a warning, the integration of rational functions can be a difficult topic to digest.
First of all, let's talk about rational function. A rational function is obtained as a ratio of two polynomials with real coefficients. Example below.
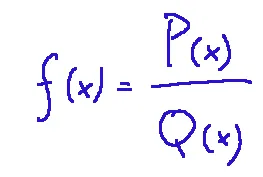
NOTE: a polynomial is an algebraic expression formed by a sum of monomial terms of the following type:
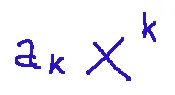
Where:
ak= coefficient belonging to a given numerical set
x = variable
k = a non-negative integer
The general form of a polynomial is as follows:
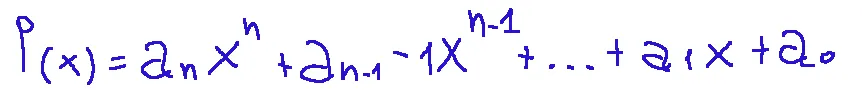
example
Here is an example of a polynomial of degree 4, principal coefficient 3, known term -5
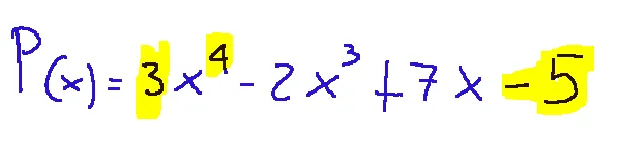
characteristics of a real function
-Domain D, i.e. all real numbers do not cancel the denominator
-As a function it has the characteristic of being continuous.
-Derivatives are rational
Here is the appearance of a rational function:
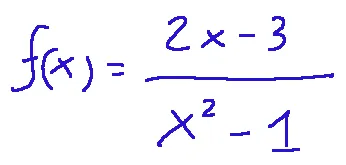
Integrations of rational functions
We have tried to transfer the concept of a rational function which in summary we can say is a ratio of polynomials.
The integral of a rational function is calculated with a procedure that is divided into three steps. These steps are called as follows:
-Division
-Decomposition into simple fractions
-Integration of each term
Exercise
If F(x) is the primitive of 2(2x2+x)/(2x-1) which is 3 in 1, then what is F(2)?
This exercise is certainly complicated, but I will try to show the steps to do it anyway.
Let's start from its description:
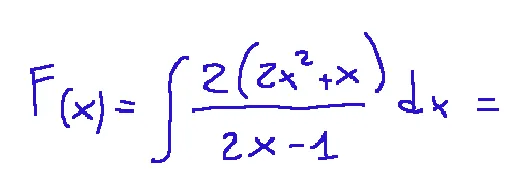
let's apply the first transformation
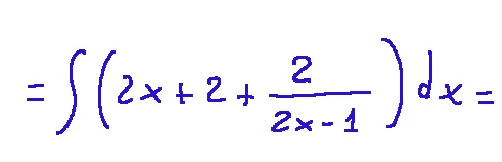
then we arrive at the form in which the constant is present C.
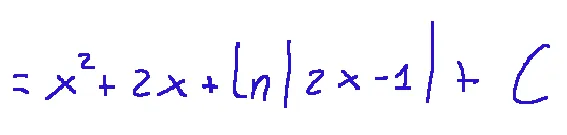
After a short reasoning we notice that F(1) = 3 gives the following condition:
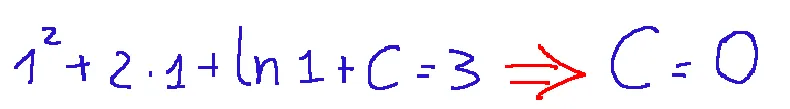
So we can write F(x)
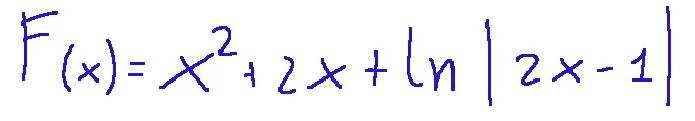
And now we calculate the function at x=2
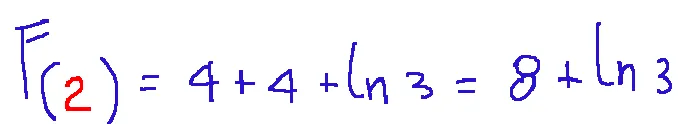
Result
the result is 8+ln3
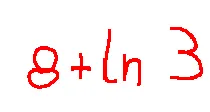
Conclusions
Integrating rational functions is useful in analytic geometry, physics, electrical engineering, and statistics.
Question
Did you know that Leonhard Euler, a Swiss mathematician and astronomer (also known as Euler) provided the practical tools for integrating rational functions that students use every day today?

ITALIAN

11-07-2025 - Analisi Matematica - Integrali di funzioni razionali [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X-60-59)
Integrali di funzioni razionali
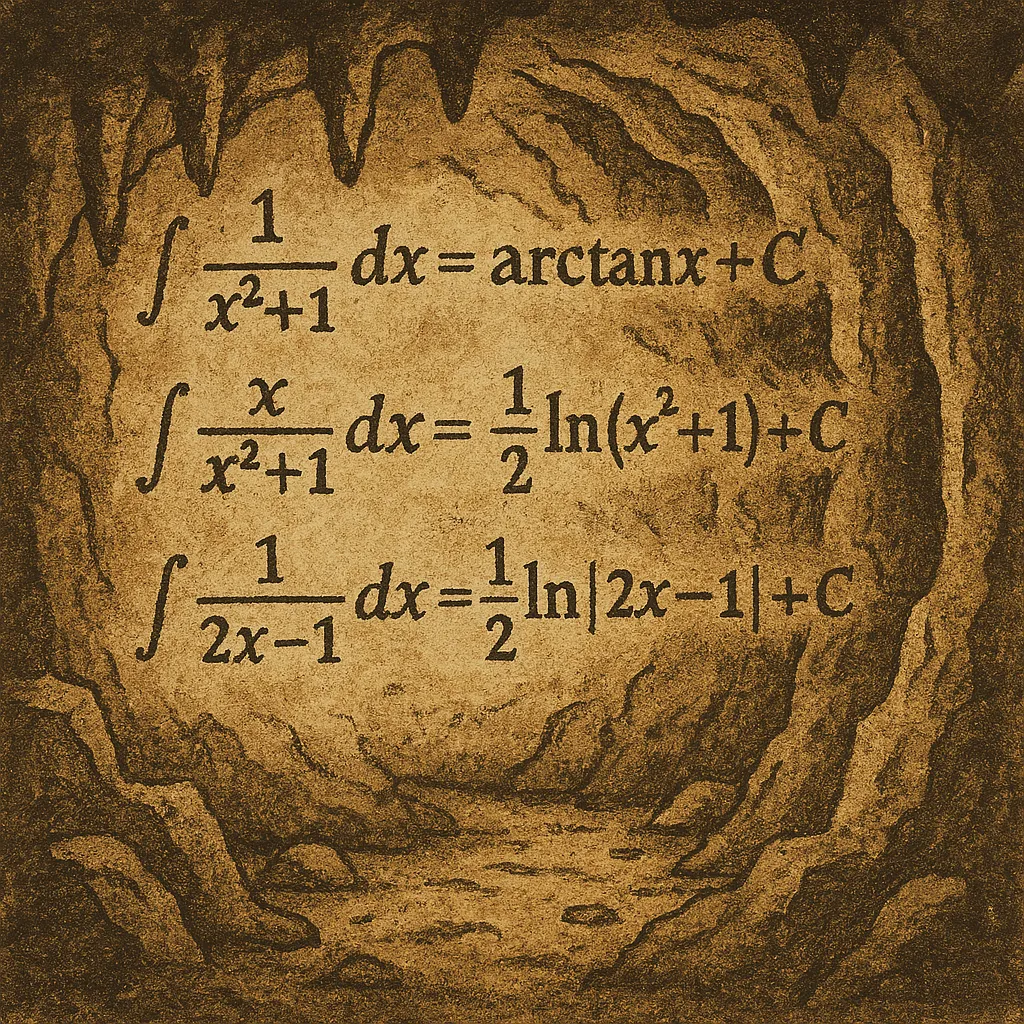
immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Partiamo subito con un avviso, l'integrazione di funzioni razionali può essere un argomento difficile da digerire.
Innanzitutto parliamo di funzione razionale. Una funzione razionale è ottenuta come rapporto di due polinomi a coefficienti reali. Esempio qui sotto.
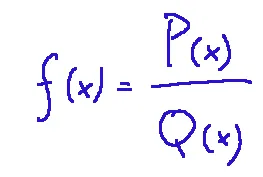
NOTA: un polinomio è un’espressione algebrica formata da una somma di termini monomî del tipo seguente:
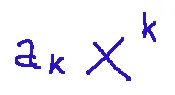
Dove:
ak= coefficiente appartenente a un dato insieme numerico
x = variabile
k = un numero intero non negativo
La forma generale di un polinomio è la seguente:
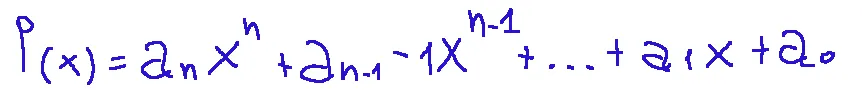
esempio
Qui di seguito l'esempio di un polinomio di grado 4, coefficiente principale 3, termine noto -5
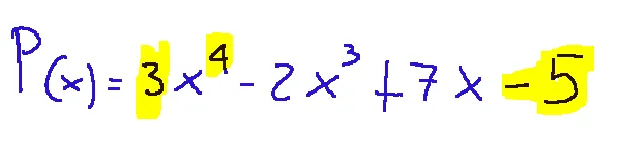
caratteristiche di una funzione reale
-Dominio D, cioè tutti i numeri reali non annullano il denominatore
-Come funzione ha la caratteristica di essere continua.
-Le derivate risultano razionali
Qui di seguito l'aspetto di una funzione razionale:
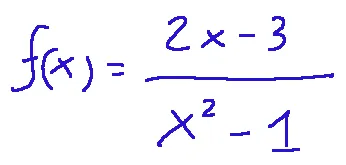
Integrazioni di funzioni razionali
Abbiamo cercato di trasferire il concetto di una funzione razionale che in sintesi possiamo dire che è un rapporto di polinomi.
L'integrale di una funzione razionale si calcola con un procedimento che è diviso in tre passi. Questi passi sono chiamati come segue:
-Divisione
-Decomposizione in fratti semplici
-Integrazione di ogni termine
Esercizio
Se F(x) è la primitiva di 2(2x2+x)/(2x-1) che vale 3 in 1, allora F(2) quanto vale?
Questo esercizio è sicuramente complicato, ma provo comunque a mostrare i passi per svolgerlo.
Partiamo dalla sue descriizione:
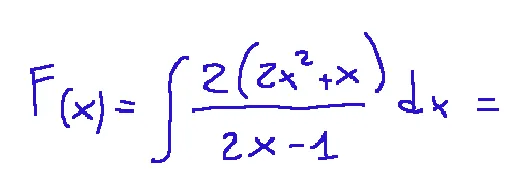
applichiamo la prima trasformazione
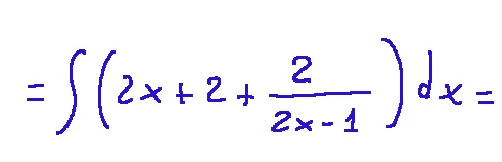
poi arriviamo alla forma in cui è presente la costante C.
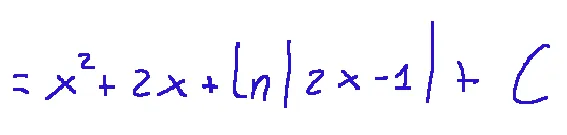
Dopo un breve ragionamento notiamo che F(1) = 3 fornisce la seguente condizione:
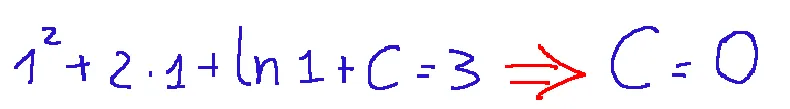
Quindi possiamo scrivere F(x)
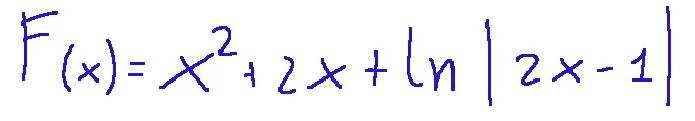
Ed ora calcoliamo la funzione in x=2
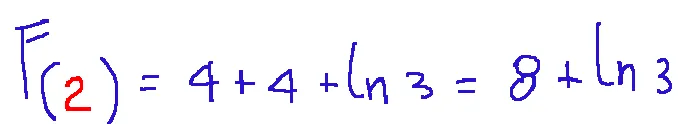
Risultato
il risultato è 8+ln3
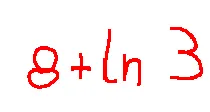
Conclusioni
L’integrazione di funzioni razionali è utile nell'ambito della geometria analitica, in fisica, in elettrotecnica e nella statistica.
Domanda
Lo sapevate che Leonhard Euler, matematico e astronomo svizzero (conosciuto anche come Eulero) fornì gli strumenti pratici per integrare le funzioni razionali che gli studenti usano oggi quotidianamente?
THE END