
~~~ La versione in italiano inizia subito dopo la versione in inglese ~~~
ENGLISH

31-07-2025 - Operations Research - Integer Linear Programming [EN]-[IT]
With this post, I would like to provide a brief introduction to the topic in question.
(code notes: X_79)
Integer Linear Programming

Image created with artificial intelligence, the software used is Microsoft Copilot
Introduction
We've previously discussed linear programming in general. In this article, I'd like to delve into a specific topic in greater detail: integer linear programming.
Linear Programming
Linear programming (sometimes abbreviated as LP) is simply an optimization problem in which the objective is to maximize or minimize a linear function in the decision variables of the problem.
In linear programming, the set of feasible solutions is defined by a system of linear equations or inequalities in the decision variables (also called constraints).
Integer Linear Programming
An integer linear programming problem is a linear programming problem in which the variables are constrained to take integer values (i.e., in the set ℤ).
Linear Programming {0,1}
A programming {0,1} problem is a linear programming problem in which the variables are constrained to take binary values in the set {0,1} and represent the possibility of an event occurring or not.
Linear Programming Exercise {0,1}
A small company must decide whether to invest in three projects. Based on the rule that {0,1} represents the possibility of an event occurring or not, we assume that each project can be approved (1) or postponed (0). Let's imagine that the projects have an estimated cost and profit. The available budget is 5 units.
We then introduce the cost and profit variables, meaning that each project will have a cost and a profit. For example, project 1 will have a cost of 2 and a profit of 3, project 2 will have a cost of 3 and a profit of 4, while project 3 will have a cost of 1 and a profit of 2.
In all of this, remember that we have a budget of 5.
... but let's not waste time talking... what is our goal? Let's always keep in mind that our goal is to maximize profit while respecting the budget constraint.
Procedure
Let's take the initial data and create a table.
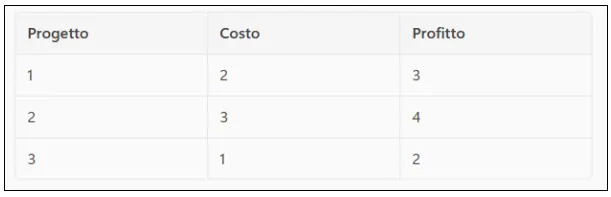
We identify the decision variables as x1, x2, and x3, and they belong to {0,1}. Recall that 1 means project approval, and 0 means project non-approval.
What we just wrote mathematically translates as follows:

Our objective function will be to maximize Z based on the following request:

Where
3x1 = 3 (profit of project 1), x1 (project variable 1, which can be 0 or 1)
While our budget constraint will be mathematically expressed by the following inequality:
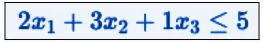
Where
2x1 = 2 (cost of project 1) x1 (variable of project 1, which can be 0 or 1)
Now we need to examine all the possibilities, and in this case we can write everything in a table.
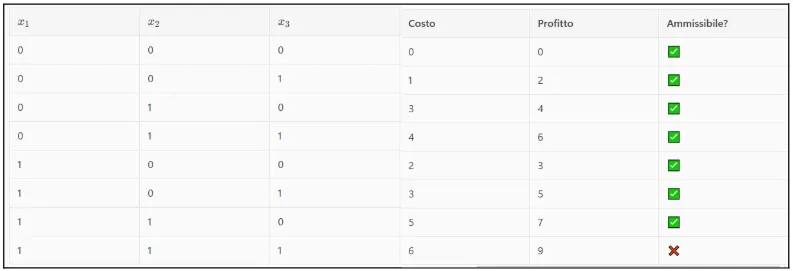
Let's take an example with the 4th row:
We have x1 as 0, while x2 and x3 are set to 1, so in the cost column we have that the cost will be that of x2 + x3, i.e., 4, while the profit will be the sum of the profits of project 2 and project 3, i.e., 6. Remember that the admissible solutions are those with a budget less than or equal to 5.
If we check, there is only one solution that has a cost greater than 5, and it is the last solution with all the approved projects, i.e., with x1, x2, and x3 all set to 5. 1.
Optimal Solution
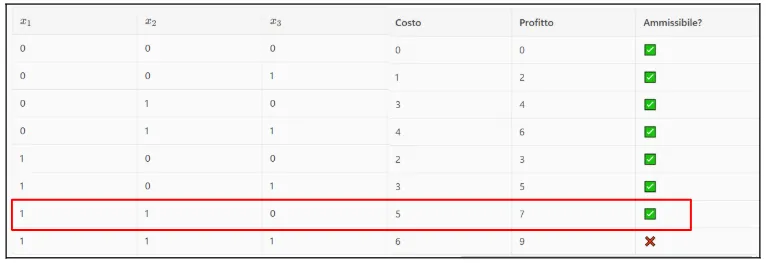
Our optimal solution will be the one that generates the greatest profit while respecting the budget constraint.
According to the table, the solution with x1=1, x2=2, and x3=0 yields a maximum profit of 7 and satisfies the budget constraint (less than or equal to 0).
Below is the table indicating the optimal solution.
Conclusions
Linear programming {0,1} is a form of combinatorial optimization in which the decision variables can take only two values, 1 or 0. This type of programming is perfect for helping decision-making in problems where decisions are of the yes/no or true/false type.
Question
Several mathematical minds have contributed to linear programming {0,1} in the past, but an undisputed pioneer was Soviet scientist Leonid Kantorovich. Did you know that Kantorovich introduced the first concepts of linear programming for economic planning in 1939? Did you also know that Kantorovich won the Nobel Prize in Economics in 1975?

ITALIAN

31-07-2025 - Ricerca operativa - Programmazione Lineare Intera [EN]-[IT]
Con questo post vorrei dare una breve istruzione a riguardo dell’argomento citato in oggetto
(code notes: X_79)
Programmazione Lineare Intera

immagine creata con l’intelligenza artificiale, il software usato è Microsoft Copilot
Introduzione
Abbiamo parlato in precedenza di programmazione lineare in maniera generale. In questo articolo vorrei entrare più nel dettaglio soprattutto in un argomento particolare, la programmazione lineare intera.
Programmazione lineare
La programmazione lineare (a volte abbreviato come PL) non è altro che un problema di ottimizzazione in cui l’obiettivo è massimizzare o minimizzare una funzione lineare nelle variabili di decisione del problema.
Nella programmazione lineare l’insieme delle soluzioni ammissibili sono definite da un sistema di equazioni o disequazioni lineari nelle variabili di decisione (chiamate anche vincoli)
Programmazione lineare intera
Un problema di programmazione lineare intera è un problema di programmazione lineare in cui le variabili sono vincolate ad assumere valori interi (cioè nell’insieme ℤ)
Programmazione lineare {0,1}
Un problema di programmazione {0,1} è un problema di programmazione lineare in cui le variabili sono vincolate ad assumere valori binari nell’insieme {0,1} e rappresentano la possibilità che un evento si verifichi oppure no.
Esercizio di programmazione lineare {0,1}
Una piccola azienda dve decidere se investire in 3 progetti. Basandosi sulla regola che {0,1} rappresentano la possibilità che un evento si verifichi oppure no, pensiamo che ogni progetto possa essere approvato (1) o rimandato (0). Immaginiamo che i progetti abbiano un costo e un profitto stimato. Il budget disponibile è di 5 unità.
Quindi introduciamo le variabili di costo e profitto, cioè ogni progetto avrà un costo ed un profitto. Ad esempio il progetto 1 avrà un costo di 2 ed un profitto di 3, il progetto 2 avrà un costo di 3 ed un profitto di 4, mentre il progetto 3 avrà un costo di 1 ed un profitto di 2.
In tutto questo ricordiamo che abbiamo un budget di 5.
.. ma non perdiamoci in chiacchere.. qual è il nostro obiettivo? Teniamo sempre bene in mente che il nostro obiettivo è quello di massimizzare il profitto rispettando il vincolo di budget.
Svolgimento
Prendiamo i dati di partenza e costruiamo una tabella.

Le variabili decisionali le identifichiamo come x1,x2 e x3 ed appartengono a {0,1}, ricordiamo che 1 significa approvazione del progetto, 0 non approvazione del progetto.
Quello che abbiamo appena scritto matematicamente si traduce come segue:

La nostra funzione obiettivo sarà massimizzare Z in base alla seguente richiesta

Dove
3x1 = 3 (profitto del progetto 1), x1 (variabile del progetto 1 che può essere 0 oppure 1)
Mentre il nostro vincolo di budget sarà matematicamente espresso dalla seguente disequazione
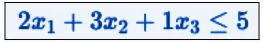
Dove
2x1 = 2 (costo del progetto 1) x1 (variabile del progetto 1 che può essere 0 oppure 1)
Ora dobbiamo esaminare tutte le possibilità ed in questo caso possiamo scrivere tutto su una tabella.

Facciamo un esempio con la 4 riga:
Abbiamo che x1 è 0, mentre x2 e x3 sono impostate ad 1, quindi nella colonna dei costi abbiamo che il costo sarà quello di x2+x3, cioè 4, mentre il profitto sarà la somma del profitto del progetto 2 e del progetto 3, cioè 6. Ricordiamo che le soluzioni ammissibili sono quelle che hanno un budget minore o uguale a 5
Se andiamo a verificare c’è solo una soluzione che ha un costo superiore a 5 ed è l’ultima soluzione con tutti i progetti approvati, cioè con x1, x2 e x3 tutti impostati ad 1.
Soluzione ottima
La nostra soluzione ottimale sarà quella che genererà il maggior profitto rispettando appunto il vincolo di budget.
Secondo la tabella la soluzione con x1=1, x2=2 e x3=0 da un profitto massimo di 7 e rispetta appunto il vincolo di budget (minore o uguale 0)
Qui di seguito riporto la tabella con indicato la soluzione ottimale

Conclusioni
La programmazione lineare {0,1} è una forma di ottimizzazione combinatoria in cui le variabili decisionali possono assumere solo due valori, 1 o 0. Questa tipologia di programmazione è perfetta per aiutare a prendere delle decisioni in problemi in cui le decisioni sono del tipo si/no oppure vero/falso.
Domanda
Diverse menti matematiche in passato hanno dato il loro contributo alla programmazione lineare {0,1}, ma un indiscusso pioniere è stato il sovietico Leonid Kantorovich. Lo sapevate che Kantorovich introdusse nel 1939 i primi concetti di programmazione lineare per la pianificazione economica? Sapevate anche che Kantorovich prese anche un premio Nobel per l’economia nel 1975?
THE END