This post is part two in a two part series on hash-based signatures. You can find part one here if you missed it.
As you may know, I recently entered a proposal into the HIVE proposal system, for starting work on two libraries meant to aid HIVE in the future transition from the current elliptic-curve signatures (ECDSA) to post-quantum-ready hash based signatures.
If you are on HIVE and haven't voted to aprove the funding of my proposal yet, please go to its proposal page on peakd and push the 'SUPPORT NOW' button.
In part one of this series we showed how to create one-time hash-based signatures with a one-time pub/priv keypair using the programming language Python, and we looked into the use of a dual WOTS chain for attenuating the size concequences of using a hash based signature scheme.
In this post, we are going to be taking what we did in the previous post, and use these one-time signatures and WOTS chains as the basis for creating a many-use signing key.
A hash of hashes
Remember our public key for signing one 16 bit checksum with looked something like this:
BB51DC64 9210F525 E9D38EE6 C092A7A7
Basically these are four different public keys, used to validate the signature of 4 out of our bits at a time. Now what if we take the two first parts together and calculate the hash. Then take the second two together and calculate the hash of those. Then take the resulting two hashes together and take the hash of those. We end up with a single, in this case 16 bit hash.
def flatten_pubkey(key):
rval = list()
for subkey in key:
rval.append(subkey[0])
rval.append(subkey[1])
return rval
def reduce(key):
part1 = key[0]
part2 = key[1]
if len(key) > 2:
breakpoint = int(len(key)/2)
part1 = reduce(key[:breakpoint])
part2 = reduce(key[breakpoint:])
return digest(part1 + part2)
reduced_pubkey = reduce(flatten_pubkey(derived_pubkey))
print("pubkey:", reduced_pubkey.hex().upper())
pubkey: 173C
As discussed in the previous post, the use of a 16 bit CRC16 hash for signatures is silly, but given that these posts are meant to demonstrate how the algorithms work at a basic level, the use of CRC16 for now is convenient for educational purposes. Just remember to never ever use CRC16 as a secure hash in production.
Now lets look how we can use this reduced size public key for validating a signature.
def validate_digest_v3(dgst, signature, reduced_pubkey):
pseudo_pubkey = list()
for nibbleno in range(0,4):
count2 = int(dgst.hex()[nibbleno],16)
count1 = 15 - count2
val1 = signature[nibbleno][0][0:2]
val2 = signature[nibbleno][0][2:]
for _ in range (0, count1+1):
val1 = digest(val1)
for _ in range (0, count2+1):
val2 = digest(val2)
pseudo_pubkey.append(val1)
pseudo_pubkey.append(val2)
reduced_pseudo_pubkey = reduce(pseudo_pubkey)
return reduced_pubkey == reduced_pseudo_pubkey
validate_digest_v3(checksum, derived_signature, reduced_pubkey)
True
The use of this little trick, taking the hash of two values, than taking two resulting hashes and again taking the hash of these, all the way until there is only one hash value left, is called a Merkle Tree. We'll be seeing one more of these before the end of this post.
A collection of keys
Now as to explain and show the creation of a multi-use key, let us start simply by creating a small collection of 32 one time signature secret keys.
def seed_to_privkey_v3(seed):
rval = list()
for keyno in range(0,32):
rval.append(list())
for nibbleno in range(0,4):
rval[-1].append(list())
for direction in range(0,2):
rval[-1][-1].append(digest(chr(keyno).encode() +
chr(nibbleno).encode() +
chr(direction).encode() + seed))
return rval
def key_to_hex_v3(key):
rval = ""
for subkey in key:
for pkey in subkey:
for val in pkey:
rval += val.hex().upper()
rval += " "
return rval
seed3 = get_random()
privkey3 = seed_to_privkey_v3(seed3)
print(key_to_hex_v3(privkey3))
B5C882F8 C37CF44C 58A06F90 2E141924 1F9928A9 692D5E1D F2F1C5C1 8445B375 F14BC67B 87FFB0CF 1C232B13 6A975DA7 5B1A6C2A 2DAE1A9E B6728142 C0C6F7F6 3CCE0BFE 4A7A7D4A D1A6E696 A7129022 969FA1AF E02BD71B 7BF74CC7 0D433A73 784D4F7D 0EF939C9 9525A215 E391D4A1 D21CE52C A4A89398 3F740844 49C07EF0 B7E580D5 C151F661 5A8D6DBD 2C391B09 1DB42A84 6B005C30 F0DCC7EC 8668B158 F366C456 85D2B2E2 1E0E293E 68BA5F8A 59376E07 2F8318B3 B45F836F C2EBF5DB 3EE309D3 48577F67 D38BE4BB A53F920F 94B2A382 E206D536 79DA4EEA 0F6E385E 7A604D50 0CD43BE4 9708A038 E1BCD68C D031E701 A68591B5 3D590A69 4BED7CDD B19286A2 C726F016 5CFA6BCA 2A4E1D7E 1BC32CF3 6D775A47 F6ABC19B 801FB72F F511C221 83A5B495 18792F49 6ECD59FD 5F406870 29F41EC4 B2288518 C49CF3AC 38940FA4 4E207910 D5FCE2CC A3489478 92C5A5F5 E471D341 7FAD489D 09193E29 7C174B27 0AA33D93 917FA64F E7CBD0FB D646E176 A0F297C2 3B2E0C1E 4D9A7AAA B3BF848F C50BF23B 5ED769E7 28631F53 19EE2EDE 6F5A586A F486C3B6 8232B502 F73CC00C 8188B6B8 1A542D64 6CE05BD0 5D6D6A5D 2BD91CE9 B0058735 C6B1F181 3AB90D89 4C0D7B3D D7D1E0E1 A1659655 90E8A7D8 E65CD16C 7D804AB0 0B343C04 7E3A490A 088E3FBE 9352A462 E5E6D2D6 D46BE35B A2DF95EF 39030E33 4FB77887
We can create public keys from these using the double WOTS chain we discussed in the previous post, and we can then use the merkle tree trick to reduce the resulting keys to smaller size hashes.
def privkey_to_pubkey_v3(privkey):
rval = list()
for subkey in privkey:
rval.append(reduce(flatten_pubkey(privkey_to_pubkey_v2(subkey))))
return rval
def hex_bytelist(pubkey):
rval = ""
for subkey in pubkey:
if rval:
rval += " "
rval += subkey.hex().upper()
return rval
pubkey3 = privkey_to_pubkey_v3(privkey3)
print(hex_bytelist(pubkey3))
F19E 3FB1 7DE1 B3CE F941 376E 753E BB11 E020 2E0F 6C5F A270 E8FF 26D0 6480 AAAF D2E2 1CCD 5E9D 90B2 DA3D 1412 5642 986D C35C 0D73 4F23 810C CB83 05AC 47FC 89D3
We could do this one more time to get a single Merkle Tree root for a combined key.
pubkey4 = reduce(pubkey3)
print(pubkey4.hex().upper())
3572
This won't however cut it at this point, we need to remember intermediate merkle tree results if we want to use this top level Merkle Tree for a multi-signature signing key.
def pubkey_to_merkletree(key, prefix=""):
drval = dict()
part1 = key[0]
part2 = key[1]
if len(key) > 2:
breakpoint = int(len(key)/2)
part1, dpart1 = pubkey_to_merkletree(key[:breakpoint], prefix + "0")
part2, dpart2 = pubkey_to_merkletree(key[breakpoint:], prefix + "1")
for key in dpart1:
drval[key] = dpart1[key]
for key in dpart2:
drval[key] = dpart2[key]
rval = digest(part1 + part2)
if prefix:
drval[prefix] = rval
if len(key) == 2:
drval[prefix + "0"] = part1
drval[prefix + "1"] = part2
return rval, drval
return rval, drval
def print_mt(mt):
for key in mt:
print(key, ":", mt[key].hex().upper())
pubkey4, mtree = pubkey_to_merkletree(pubkey3)
print(pubkey4.hex().upper())
print()
print_mt(mtree)
3572
0000 : 2890
00000 : F19E
00001 : 3FB1
0001 : 9F2E
00010 : 7DE1
00011 : B3CE
000 : 07CD
0010 : 57CD
00100 : F941
00101 : 376E
0011 : E073
00110 : 753E
00111 : BB11
001 : 1EF6
00 : 9A2E
0100 : D62A
01000 : E020
01001 : 2E0F
0101 : 6194
01010 : 6C5F
01011 : A270
010 : 35BB
0110 : A977
01100 : E8FF
01101 : 26D0
0111 : 1EC9
01110 : 6480
01111 : AAAF
011 : 2C80
01 : 4CA1
0 : DE99
1000 : C5C5
10000 : D2E2
10001 : 1CCD
1001 : 727B
10010 : 5E9D
10011 : 90B2
100 : 6321
1010 : BA98
10100 : DA3D
10101 : 1412
1011 : 0D26
10110 : 5642
10111 : 986D
101 : 7A1A
10 : 2711
1100 : 3B7F
11000 : C35C
11001 : 0D73
1101 : 8CC1
11010 : 4F23
11011 : 810C
110 : 5157
1110 : 4422
11100 : CB83
11101 : 05AC
1111 : F39C
11110 : 47FC
11111 : 89D3
111 : 486C
11 : F19E
1 : 50B7
To understand why we need these intermediate nodes to sign our message digest, lets have a little look at a simple tree graphically.
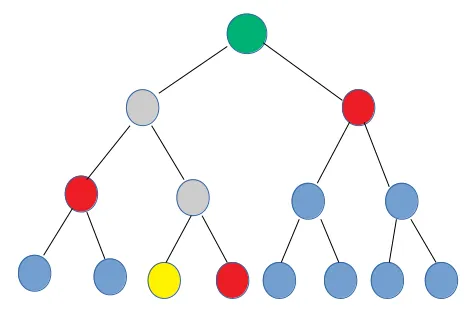
Imagine the yellow dot would be our former merkle-tree reduced WOTS chain public key. Now realize we want to use the green dot as new public key that we can validate multiple signaturer against (one for each of the dots on the bottom. We can do so by adding the intermediate hashes of the red dots to our signature. If our signature checking gets us the yellow dot, we can recreate the grey and the green dot from just the red dots without needing any of the blue dots.
Let's see how this works. We create a signature header containing the red dots for signature number 17.
def mt_index_to_sigheader(mtree, index):
rval = list()
rval.append(b'\x00' + chr(index).encode())
bitindex = BitArray(hex(index)).bin[-5:]
print("+ ",bitindex, "(", "00" + chr(index).encode().hex() ,"hex)")
for index in range(0,5):
prefix = bitindex[0:index]
thisbit = bitindex[index]
if thisbit == "1":
print(" *", prefix + "0 :", mtree[prefix + "0"].hex().upper())
rval.append(mtree[prefix + "0"])
else:
print(" *", prefix + "1 :", mtree[prefix + "1"].hex().upper())
rval.append(mtree[prefix + "1"])
return rval
sig_index = 17
mt_signature_header = mt_index_to_sigheader(mtree, sig_index)
print()
print("mt-header:", hex_bytelist(mt_signature_header))
+ 10001 ( 0011 hex)
* 0 : DE99
* 11 : F19E
* 101 : 7A1A
* 1001 : 727B
* 10000 : D2E2
mt-header: 0011 DE99 F19E 7A1A 727B D2E2
Now we use this as a header for our actual number 17 signature
def sign_digest_v3(dgst, privkey, mtree, index):
pkey = privkey[index]
rval = [mt_index_to_sigheader(mtree, index)]
for nibbleno in range(0,4):
rval.append(list())
rval[-1].append(sign_nibble(dgst, pkey, nibbleno))
return rval
signature_v3 = sign_digest_v3(checksum, privkey3, mtree, sig_index)
print()
print("signature:", key_to_hex(signature_v3))
+ 10001 ( 0011 hex)
* 0 : DE99
* 11 : F19E
* 101 : 7A1A
* 1001 : 727B
* 10000 : D2E2
signature: 0011DE99F19E7A1A727BD2E2 14FA9CF7 7306C395 61787277 D4B80A0B
Finaly let's look how we can use this info to check our signature.
import copy
def reconstruct_merkle_root(nodes, bitindex, reduced_pseudo_pubkey):
res = reduced_pseudo_pubkey
for index in range(0,len(bitindex)):
if bitindex[index] == "0":
res = digest(res + nodes[index])
else:
res = digest(nodes[index] + res)
return res
def validate_digest_v3(dgst, pubkey, signature):
sig = copy.deepcopy(signature)
header = sig.pop(0)
bindex = header.pop(0)
index = struct.unpack(">H", bindex)[0]
pseudo_pubkey = list()
for nibbleno in range(0,4):
count2 = int(dgst.hex()[nibbleno],16)
count1 = 15 - count2
val1 = sig[nibbleno][0][0:2]
val2 = sig[nibbleno][0][2:]
for _ in range (0, count1+1):
val1 = digest(val1)
for _ in range (0, count2+1):
val2 = digest(val2)
pseudo_pubkey.append(val1)
pseudo_pubkey.append(val2)
reduced_pseudo_pubkey = reduce(pseudo_pubkey)
bitindex = BitArray(hex(index)).bin[-5:]
mt_root_candidate = reconstruct_merkle_root(list(reversed(header)), list(reversed(list(bitindex))), reduced_pseudo_pubkey)
return mt_root_candidate == pubkey
validate_digest_v3(checksum, pubkey4, signature_v3)
I hope you are still with me. Its been a bit of a ride, but we now have succesfully created a signing key that can be used 32 times. A silly CRC16 based signing key that has no real use, but the concepts for making a real signing key have all been discussed.
Putting it all together.
Let's put all of this together in a bit of semi-usable code. Its a bit of a large chunk of code, but if you look carefully you will see all of the things we discussed. Don't mind the details.
import math
import time
import os
import struct
import random
from hashlib import blake2b
from bitstring import BitArray
from crc16 import crc16xmodem as crc16int
def get_random():
return struct.pack(">H",random.randint(0,256*256-1))
def digest(data):
return struct.pack(">H",crc16int(data))
def asbits(data):
return BitArray(bytes=data).bin
class Crc16:
def __init__(self):
self.bitcount = 16
def __call__(self, data, key=b""):
return struct.pack(">H",crc16int(data + key))
class Blake2B196:
def __init__(self):
self.bitcount = 192
def __call__(self, data, key=b""):
return blake2b(data, digest_size=24, key=key).digest()
def generate_seed(hashfunction):
return os.urandom(int(hashfunction.bitcount/8))
def flatten_pubkey(key):
rval = list()
for subkey in key:
rval.append(subkey[0])
rval.append(subkey[1])
return rval
def pubkey_to_merkletree(key, hashfunction, prefix=""):
drval = dict()
part1 = key[0]
part2 = key[1]
if len(key) > 2:
breakpoint = int(len(key)/2)
part1, dpart1 = pubkey_to_merkletree(key[:breakpoint], hashfunction, prefix + "0")
part2, dpart2 = pubkey_to_merkletree(key[breakpoint:], hashfunction, prefix + "1")
for key in dpart1:
drval[key] = dpart1[key]
for key in dpart2:
drval[key] = dpart2[key]
rval = hashfunction(part1, part2)
if prefix:
drval[prefix] = rval
if len(key) == 2:
drval[prefix + "0"] = part1
drval[prefix + "1"] = part2
return rval, drval
def reconstruct_merkle_root(hashfunction, nodes, bitindex, reduced_pseudo_pubkey):
res = reduced_pseudo_pubkey
for index in range(0,len(bitindex)):
if bitindex[index] == "0":
res = hashfunction(res, nodes[index])
else:
res = hashfunction(nodes[index], res)
return res
class PrivateKey:
def __init__(self, seed, hashfunction, wotsbits, merkledepth, start=0):
self.next_signum = start
self.hashfunction = hashfunction
self.wotsbits = wotsbits
self.merkledepth = merkledepth
self.subkeys_per_key = math.ceil(hashfunction.bitcount/wotsbits)
self.key_count = int(math.pow(2,merkledepth))
# generate secret key from seed.
self.private_key = list()
for index in range(0, self.key_count):
onekey = list()
for index2 in range(0,self.subkeys_per_key):
wotspair = list()
for direction in [b"L", b"R"]:
wotspair.append(self.hashfunction(str(index).encode() +
direction +
str(index2).encode(), key=seed))
onekey.append(wotspair)
self.private_key.append(onekey)
# generate the big pubkey from private key
public_key = list()
first = True
for onekey in self.private_key:
onekey_pub = list()
for wotspair in onekey:
public_wotspair = list()
for subkey in wotspair:
result = subkey
for ind1 in range(0,int(math.pow(2,self.wotsbits))):
result = self.hashfunction(result)
public_wotspair.append(result)
first_chain = False
onekey_pub.append(public_wotspair)
public_key.append(onekey_pub)
first = False
# reduce the public key size
medium_public_key = list()
for big_pubkey in public_key:
pkey, _ = pubkey_to_merkletree(flatten_pubkey(big_pubkey), hashfunction)
medium_public_key.append(pkey)
# Turn remaining pubkey into a merkle tree and root
self.public_key, self.merkletree = pubkey_to_merkletree(medium_public_key, hashfunction)
def sign_digest(self, digest):
if self.next_signum >= self.key_count:
raise RuntimeError("Private key has been exhausted")
# Get the current private key
private_key = self.private_key[self.next_signum]
# Convert the digest to a list of integers for signing.
digest_bits = list(BitArray(bytes=digest).bin)
bitlists = list()
while len(digest_bits) > self.wotsbits:
bitlists.append(digest_bits[:self.wotsbits])
digest_bits = digest_bits[self.wotsbits:]
bitlists.append(digest_bits)
numlist = list()
for bits in bitlists:
num = 0
for bit in bits:
num *= 2
if bit == "1":
num += 1
numlist.append(num)
# Create the signature body
signature_body=list()
for index in range(0,len(numlist)):
count1 = numlist[index]
count2 = int(math.pow(2,self.wotsbits)) - count1 - 1
val1 = private_key[index][0]
val2 = private_key[index][1]
for _ in range (0, count1):
val1 = self.hashfunction(val1)
for _ in range (0, count2):
val2 = self.hashfunction(val2)
signature_body.append([val1,val2])
# Create the merkletree signature header
signature_header_mt = list()
bitindex = BitArray("{0:#0{1}x}".format(self.next_signum,34)).bin[-self.merkledepth:]
for index in range(0,self.merkledepth):
prefix = bitindex[0:index]
thisbit = bitindex[index]
if thisbit == "1":
signature_header_mt.append(self.merkletree[prefix + "0"])
else:
signature_header_mt.append(self.merkletree[prefix + "1"])
# encode the key index
bindex = struct.pack(">H",self.next_signum)
# Compose the signature from:
# * pubkey
# * key-index
# * merkle-tree header
# * wots signatures
signature = b""
signature += self.public_key
signature += bindex
for mtnode in signature_header_mt:
signature += mtnode
for wotspair in signature_body:
for wotsval in wotspair:
signature += wotsval
self.next_signum += 1
return signature
def sign_message(self, message):
msg_digest = self.hashfunction(message)
return self.sign_digest(msg_digest)
class Validator:
def __init__(self, hashfunction, wotsbits, merkledepth):
self.hashfunction = hashfunction
self.wotsbits = wotsbits
self.merkledepth = merkledepth
def __call__(self, message, signature):
msg_digest = self.hashfunction(message)
# Convert the digest to a list of integers for signing.
digest_bits = list(BitArray(bytes=msg_digest).bin)
bitlists = list()
while len(digest_bits) > self.wotsbits:
bitlists.append(digest_bits[:self.wotsbits])
digest_bits = digest_bits[self.wotsbits:]
bitlists.append(digest_bits)
numlist = list()
for bits in bitlists:
num = 0
for bit in bits:
num *= 2
if bit == "1":
num += 1
numlist.append(num)
# Split up the signature into its parts
hlenb = int(self.hashfunction.bitcount/8)
pubkey = signature[:hlenb]
sigindex = struct.unpack(">H",signature[hlenb:hlenb+2])[0]
sigindex_bits = BitArray("{0:#0{1}x}".format(sigindex,34)).bin[-self.merkledepth:]
merkle_header = signature[hlenb+2:hlenb+2+self.merkledepth*hlenb]
merkle_header = [merkle_header[i:i+hlenb] for i in range(0, len(merkle_header), hlenb)]
signature_body = signature[hlenb+2+self.merkledepth*hlenb:]
signature_body = [signature_body[i:i+hlenb] for i in range(0, len(signature_body), hlenb)]
signature_body = [signature_body[i:i+2] for i in range(0, len(signature_body), 2)]
# Complete the double WOTS chain.
big_pubkey = list()
for index in range(0, len(numlist)):
count1 = int(math.pow(2,self.wotsbits)) - numlist[index]
count2 = numlist[index] + 1
val1 = signature_body[index][0]
val2 = signature_body[index][1]
for _ in range (0, count1):
val1 = self.hashfunction(val1)
for _ in range (0, count2):
val2 = self.hashfunction(val2)
big_pubkey.append([val1, val2])
first = False
# Reduce the wots values to a single hash
pkey, _ = pubkey_to_merkletree(flatten_pubkey(big_pubkey), self.hashfunction)
# Check the single hash with the merkle tree header.
mt_root_candidate = reconstruct_merkle_root(
self.hashfunction,
list(reversed(merkle_header)),
list(reversed(list(sigindex_bits))),
pkey)
return pubkey == mt_root_candidate, pubkey, sigindex
We'll create a private key and see how long it takes
confession = b"I shot John Fitzgerald from the grassy knoll."
hf1 = Crc16()
seed1 = generate_seed(hf1)
start1 = time.time()
pkey1 = PrivateKey(seed1, hashfunction=hf1, wotsbits=4, merkledepth=5)
print(time.time()-start1)
0.008510112762451172
Nor let's exaust our signing key and see how it goes
print(pkey1.public_key.hex().upper())
sigs = list()
for index in range(0,35):
try:
sigs.append(pkey1.sign_message(confession))
print(" *", sigs[-1].hex().upper())
except RuntimeError as exp:
print("ERROR:", exp)
48F3
* 48F300004C6D7B41CB673960044AA470E855D823C35BA6DCD35AE5C14BC9
* 48F300014C6D7B41CB673960CA6529AC503460424E87C3D7C3B86BE8A0EA
* 48F300024C6D7B41CB678EDE8835AFE988B6B8C0C8C26CCAF29EE9B28DAE
* 48F300034C6D7B41CB678EDE461A223530D700A1451E09C1E27C679B668D
* 48F300044C6D7B41D25C463D0C95B342299319E5D46922D190D2FD27D726
* 48F300054C6D7B41D25C463DC2BA3E9E91F2A18459B547DA8030730E3C05
* 48F300064C6D7B41D25CF18380EAB8DB49707906DFF0E8C7B116F1541141
* 48F300074C6D7B41D25CF1834EC53507F111C167522C8DCCA1F47F7DFA62
* 48F300084C6DB82BBBAF30C515F48A147BF84B8EED3FBEE7544AD40D6236
* 48F300094C6DB82BBBAF30C5DBDB07C8C399F3EF60E3DBEC44A85A248915
* 48F3000A4C6DB82BBBAF7064ABCBCDDEE95AD92CAAF5512A244BE1E98917
* 48F3000B4C6DB82BBBAF706465E44002513B614D2729342134A96FC06234
* 48F3000C4C6DB82B89A24F9827B4C64789B9B9CFA16C9B3C058FED9A4F70
* 48F3000D4C6DB82B89A24F98E99B4B9B31D801AE2CB0FE37156D63B3A453
* 48F3000E4C6DB82B89A2877BA314DAEC289C18EABDC7D52767C3F90F15F8
* 48F3000F4C6DB82B89A2877B6D3B573090FDA08B301BB02C77217726FEDB
* 48F300108E63FC7DDE17CE7F2F6BD175487F7809B65E1F314607F57CD39F
* 48F300118E63FC7DDE17CE7FE1445CA9F01EC0683B827A3A56E57B5538BC
* 48F300128E63FC7DDE17F826BA75E3BA7AF74A8184914911A35BD025A0E8
* 48F300138E63FC7DDE17F826745A6E66C296F2E0094D2C1AB3B95E0C4BCB
* 48F300148E63FC7D94CBDAD9934D7990212F11591EBB082F24390A2338D8
* 48F300158E63FC7D94CBDAD95D62F44C994EA93893676D2434DB840AD3FB
* 48F300168E63FC7D94CB6D671F32720941CC71BA1522C23905FD0650FEBF
* 48F300178E63FC7D94CB6D67D11DFFD5F9ADC9DB98FEA732151F8879159C
* 48F300188E638E96B097A5849B926EA2E0E9D09F09898C2267B112C5A437
* 48F300198E638E96B097A58455BDE37E588868FE8455E92977539CEC4F14
* 48F3001A8E638E96B097123A17ED653B800AB07C0210463446751EB66250
* 48F3001B8E638E96B097123AD9C2E8E7386B081D8FCC233F5697909F8973
* 48F3001C8E638E96C72C59F982F357F4B28282F430DF1014A3293BEF1127
* 48F3001D8E638E96C72C59F94CDCDA280AE33A95BD03751FB3CBB5C6FA04
* 48F3001E8E638E96C72C93DD84CFE5B566FC568A829E3F2CD4085365579D
* 48F3001F8E638E96C72C93DD4AE06869DE9DEEEB0F425A27C4EADD4CBCBE
ERROR: Private key has been exhausted
ERROR: Private key has been exhausted
ERROR: Private key has been exhausted
Now we check the results
validator = Validator(hashfunction=hf1, wotsbits=4, merkledepth=5)
for signature in sigs:
ok, pubkey, index = validator(confession, signature)
if ok:
print("Signature OK: pubkey =", pubkey.hex().upper(), " key-index =", index)
else:
print("ERROR: incorrect signature: pubkey =", pubkey.hex().upper(), " key-index =", index)
Signature OK: pubkey = 48F3 key-index = 0
Signature OK: pubkey = 48F3 key-index = 1
Signature OK: pubkey = 48F3 key-index = 2
Signature OK: pubkey = 48F3 key-index = 3
Signature OK: pubkey = 48F3 key-index = 4
Signature OK: pubkey = 48F3 key-index = 5
Signature OK: pubkey = 48F3 key-index = 6
Signature OK: pubkey = 48F3 key-index = 7
Signature OK: pubkey = 48F3 key-index = 8
Signature OK: pubkey = 48F3 key-index = 9
Signature OK: pubkey = 48F3 key-index = 10
Signature OK: pubkey = 48F3 key-index = 11
Signature OK: pubkey = 48F3 key-index = 12
Signature OK: pubkey = 48F3 key-index = 13
Signature OK: pubkey = 48F3 key-index = 14
Signature OK: pubkey = 48F3 key-index = 15
Signature OK: pubkey = 48F3 key-index = 16
Signature OK: pubkey = 48F3 key-index = 17
Signature OK: pubkey = 48F3 key-index = 18
Signature OK: pubkey = 48F3 key-index = 19
Signature OK: pubkey = 48F3 key-index = 20
Signature OK: pubkey = 48F3 key-index = 21
Signature OK: pubkey = 48F3 key-index = 22
Signature OK: pubkey = 48F3 key-index = 23
Signature OK: pubkey = 48F3 key-index = 24
Signature OK: pubkey = 48F3 key-index = 25
Signature OK: pubkey = 48F3 key-index = 26
Signature OK: pubkey = 48F3 key-index = 27
Signature OK: pubkey = 48F3 key-index = 28
Signature OK: pubkey = 48F3 key-index = 29
Signature OK: pubkey = 48F3 key-index = 30
Signature OK: pubkey = 48F3 key-index = 31
All is great.
So now, how about getting serious. What if instead of CRC16 we use a 192 bit BLAKE2 hash? What instead of 5 bits per WOTS chain we use 12? What if instead of a Merkle Tree depth of 5, we use a depth of 10?
hf2 = Blake2B196()
seed2 = generate_seed(hf2)
start2 = time.time()
pkey2 = PrivateKey(seed2, hashfunction=hf2, wotsbits=12, merkledepth=10)
print(time.time()-start2)
132.0246787071228
That is 132 seconds to create a key. We could probably improve this going multi threaded or multi process, but it should illustrate there is a price to using WOTS chains to reduce sizes.
How about signing?
print(pkey2.public_key.hex().upper())
sigs = list()
for index in range(0,17):
try:
sigs.append(pkey2.sign_message(confession))
except RuntimeError as exp:
print("ERROR:", exp)
lastsig = sigs[-1]
print(len(lastsig))
print(lastsig.hex().upper())
CF5562E51E3BB2D9B14DAC45D91E55C9D67337DFDE1A9AB9
1034
CF5562E51E3BB2D9B14DAC45D91E55C9D67337DFDE1A9AB90010DAA4EF54A2586BB4A4A66A331E94C2D1BAFE87A35CE4165C98C1B4757041FE5275EDDE76F2679893E60393DC536EF82E3A64161003934EB5A5A5D16B62A0371E2BED4942E7EB2DEAF39BEDD01CC5E9848110B1696C59119C7FA1B8B16A8AA3EA622866464EDE1E742B28DC520958335DA4E854723671E47F96089CF4BC3F443174390A3AA022D99DB93287F8BD34136AC70DD563E7DDC782E9B0653D8A92539146E2FC2BE93CFC1749F904E85C5CC496CC4930AC11B43DDEF31E7B4ACF1E542BCF96DE0BC559C3B3ECDD1C81D766D220F6B2B58286D37848EAC3D251EB7336CEA5AA8D9C71459098201470C16709A72C94176E0F0D6AC8215005584C019FB84216DC63DBFD31F6A600D0985C367D847366B6D669C536C7640049AE2085DDBE8EFACE99828685FCA75791F9855DA54196D02E187F6DF90E97691E61D31E02B0A73772A5036955AC0A6C09C4B35B37991716C0A95352267F40155AE3559F00415586D79DFD801290CD6EDC0255158607C626DA16F6EAF6783451AB0E5F4553D8ED8975AEED8864776E7E383B40035CCC593983F2D924D7E6064DBABF0823504C701C058F64E87E2F65E7A2EA5A7E3ACF9F1634C5FD35F31214A9482ED007BFC72DD4EF7ED86C2606FD3E7FAF95FA287148923975B7CFDAFEDBAD12FFA5A3057BC0C72D65B8C178586170327F524DAF11FA625DB81A53EAEF35F6327E49A356606599C56F6596A9815C1A9D10C7EF8DC662DB6B6A102CCC1174508B39EF221BD718490717C81C6AC46B918B0F8FD4842AAE3F9FB93FFCD3ECE737FA46839AEDD7B48A5A30C6D4A0816CA919D623EE88001545D949BC8BE6C38BA6D81CB913717C8760E4307B9013AB4CF531926BB4804A59F80EDED67C56F6F0FA7460CF6A07C13860C721769AE75EEC84F3060FABDBE7802C8904C22967E5244A7669D71EDC659182140DA767A8E499432591910C29A8CA5EFC7F4C1005F619A1C4F85EC7AB4A5D2E45DDF7CFDA9A6975DC537B4DEACE219F90742FC39A2DB3FF754A90A9BA189BE3E86071E8B0A3512F86895E6783E86C011DDCFD72CFBD6142B70AB2EC472913D81D01D2C9C6276DBBD3CE8130F26C0C29986E794D87380BFB8D6527263FF8697DB7916CFA38349B8BA007D7457F98E442BAC7D7D0CAD1D73229FC7E2297B5AABAD11A2DA2D875D0B8452BFE4FE792D65C19A6A4D3F4A578AFACDDA56D7FB7A0DAC24D4A8E564427FAB1C6EC46D0E6028A13E976ACF9CB8507A732F2208CAD07D941ECDECBC5402B584558EBDD852159A48DF1EA4D21A012B45BAE4D20C28A7D659BE302A010BE606C74E270646DB8EECB87C5E1CC5A1C093423BD57C3E0F5D80DAE37BB96D1B6374C159A78C144F193BF2569E45C830A891669311CBA615D8969CF304870583ECC003464C834D4823B
A 1024 byte long signature. Let's check it.
validator = Validator(hashfunction=hf2, wotsbits=12, merkledepth=10)
ok, pubkey, index = validator(confession, lastsig)
if ok:
print("Signature OK: pubkey =", pubkey.hex().upper(), " key-index =", index)
else:
print("ERROR: incorrect signature: pubkey =", pubkey.hex().upper(), " key-index =", index)
Signature OK: pubkey = CF5562E51E3BB2D9B14DAC45D91E55C9D67337DFDE1A9AB9 key-index = 16
conclusions
I hope these two posts helped you in your understanding of the basics and properties of hash based signatures at least a bit. Hash based signatures are important for a post-quantum future for blockchains like HIVE, and if you think it is important that at least some work happens on this right now, please support my proposal with your aproval.