Hi there. In this math post, I cover the basics of logarithms. This topic is more for upper year high school students (at least in the Toronto area) and is a good review for university students who need some math for the sciences.
Math images are screenshots from witeboard.com along with my Wacom tablet and stylus.

Topics
- Solve For The Unknown Exponent
- Basic Logarithm Examples
- Some Properties Of Logarithms
- Solving Exponential Equations With Logarithms
Solve For The Unknown Exponent
Let's start with simple examples when it comes to solving for unknown exponents. Two to the power of what number is equal to eight? With this question the answer is three. This is because two to the power of three is eight.
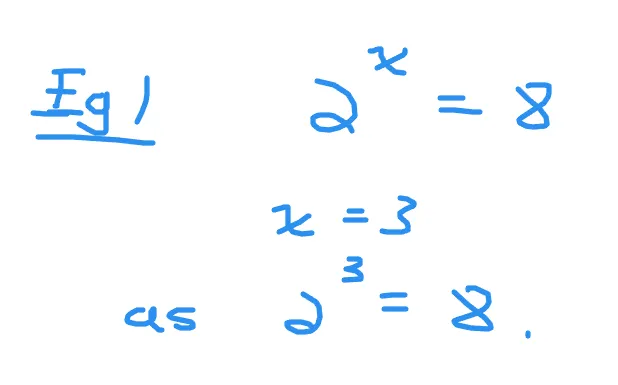
Here is another example. Ten to the power of what number is one hundredth? Ten to the power of one is ten, ten to the power of two is one hundred. A positive exponent does not work here. Consider negative exponents here. Ten to the power of negative one which is one-tenth. Ten to the power of negative two is one-hundredth. The answer here for the exponent is -2.
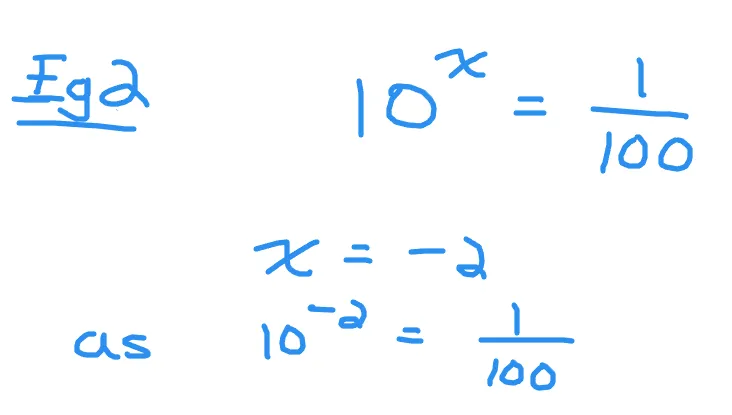
What if you have something like 7 to the power of what exponent gives 100? Seven to the power of two is 49. Seven to the power of three is 343. Three as an exponent would be too much. The answer is somewhere between two and three. You could do a guess and check method but it would be better to have an exact value. This is where logarithms come in.

To solve the problem with logarithms we take the logarithms of both sides.
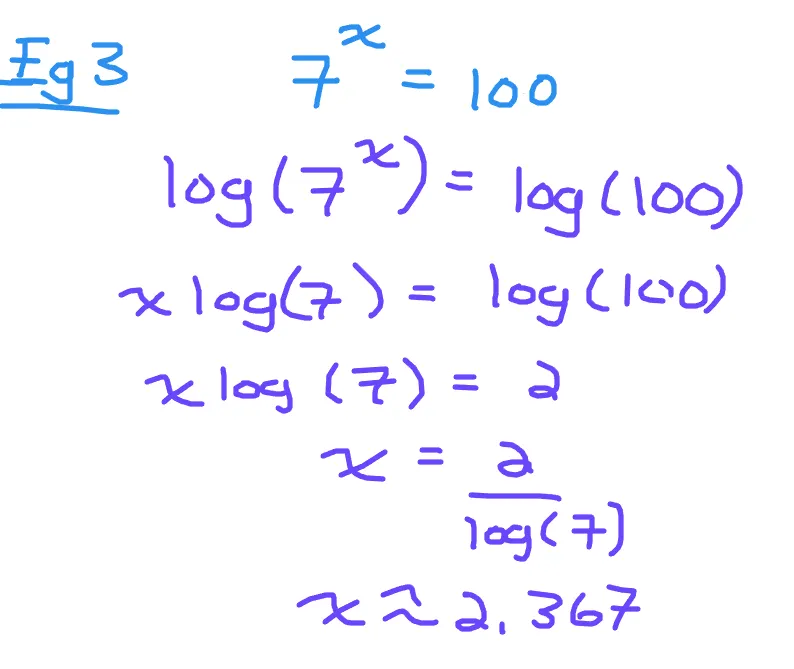
There is a property with logarithms where the exponent of x from the seven to the power of x moves to the front of the logarithm of seven. The answer of x is the logarithm of 100 divided by the logarithm of 7. The logarithm of 100 is 2. Two divided by the logarithm of seven is approximately 2.367.

Basic Logarithm Examples
In this section I present many basic examples of logarithms.
Example One
What is the logarithm of 1000? Assume base 10 for the logarithm unless stated otherwise.
Think of this question as ten to the power of what number gives one thousand. The unknown exponent or logarithm here is three as ten to the power of 3 is 1000.
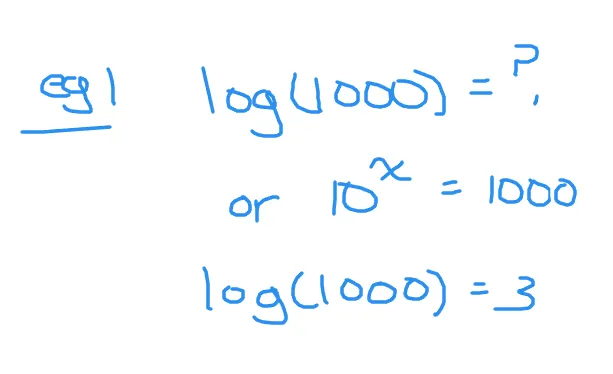
Example Two
Evaluate log(0.1).
You can rewrite 0.1 as in one tenth as a fraction. This is the same as ten to the power of negative one. The question can be thought of now as 10 to the power of what number is one tenth. The answer is negative one.
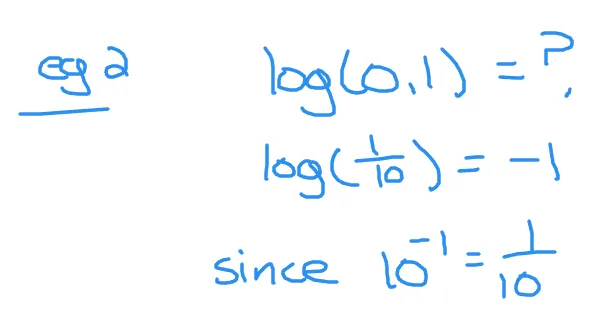
Example Three
What is the value of 2log_3(27) - 5. That is twice the logarithm of 27 with base 3 and then subtract five.
Evaluate the logarithm part first. Three to the power of what number gives 27. The answer to that logarithm is 3. Multiply this 3 with 2 and then subtract five. The answer to the expression is one.
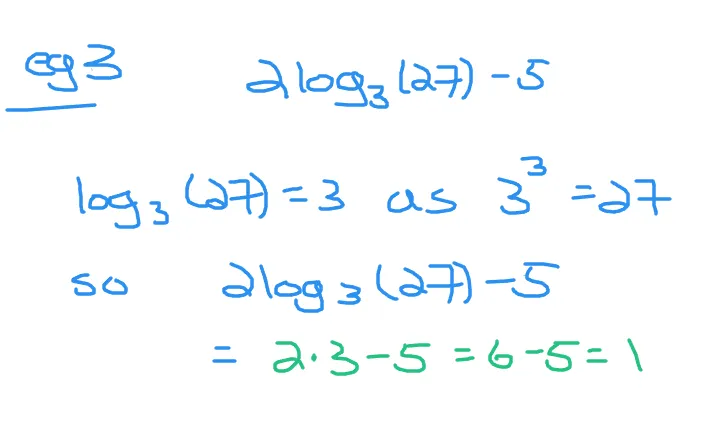
Example Four
What is the value of log_8(64) - log_2(16). This is the logarithm of 64 with base 8 minus the logarithm of 16 with base two.
Evaluate each logarithm separately. Eight to the power of something is 64. That would be 2. For the second logarithm it is two the power of something gives 16. That would be 4. After evaluating the logarithms the expression turns into 2 minus 4 to give negative two.
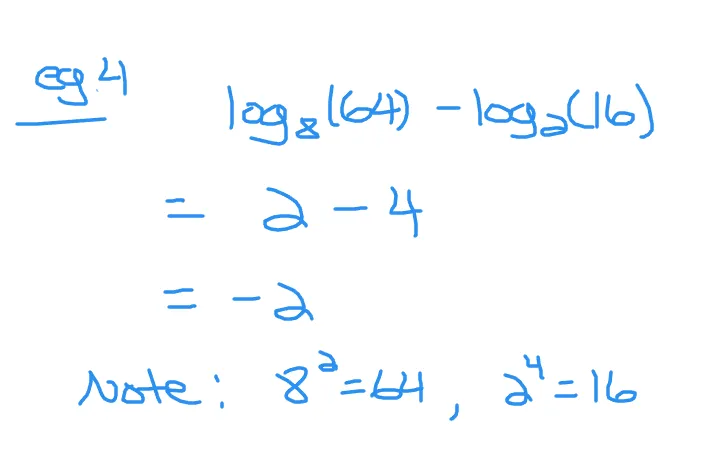

Some Properties Of Logarithms
There are some algebra properties with logarithms. Knowing, memorizing and understanding these properties does help with one's algebra for those pursuing studies in mathematics, calculus, engineering, etc.
Product Property
The logarithm of x times y is the same as the logarithm of x plus the logarithm of y. This assumes that both x and y are above zero.
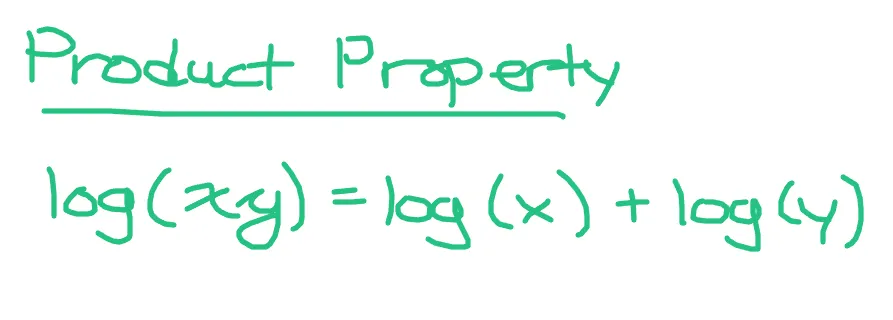
Quotient Property - Logarithm of Fractions
The logarithm of x divided y is equal to the logarithm of x minus the logarithm of y. This assumes that both x and y are above zero.
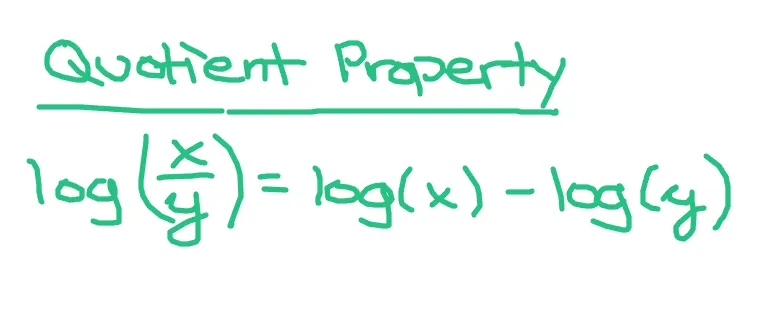
Power Property
What if the input in the logarithm has an exponent? The power property for logarithms is useful for evaluating logarithms.
The logarithm of a quantity with an exponent is equal to the exponent multiplied by the logarithm of the quantity without that exponent. You can move the exponent to the front of the logarithm. This property does look confusing in text. Refer to the screenshot below for a visual of this property.
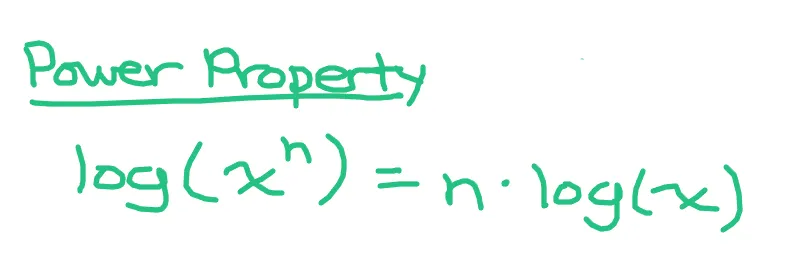
A Few Special Cases
Here are special cases with logarithms that are worth memorizing.
The logarithm with an input of one is zero. This is because anything to the power of one is zero.

The logarithm with an input that is the same as the base is one. The base to the power of one is the same base.

There is a change of base property for logarithms but I do not feature that here.
More Examples
Here are some examples that apply the logarithm properties. Note that if there is no subscript on the logarithm you can assume that the base is 10.
Example One
Simplify log(100x).
Use the product property as the input is a product of 100 times x. Log of 100 is two.
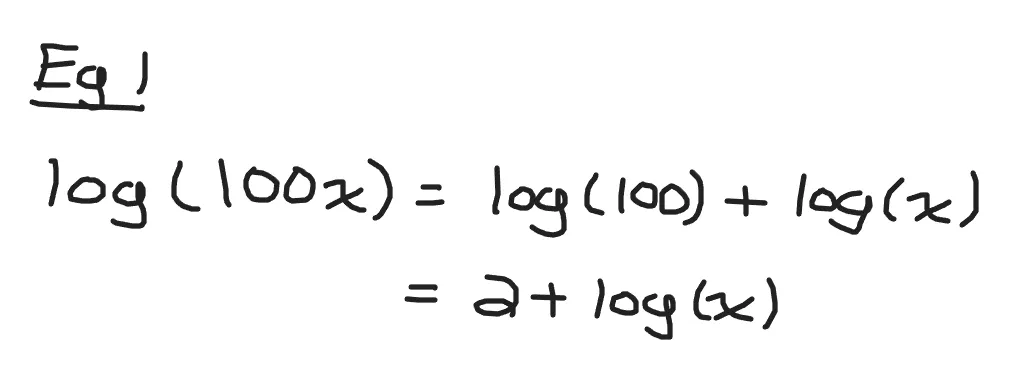
Example Two
Simplify log(x^2/10).
Use the quotient property as the input for the logarithm is a fraction. This yields the logarithm of x-squared minus the logarithm of 10.
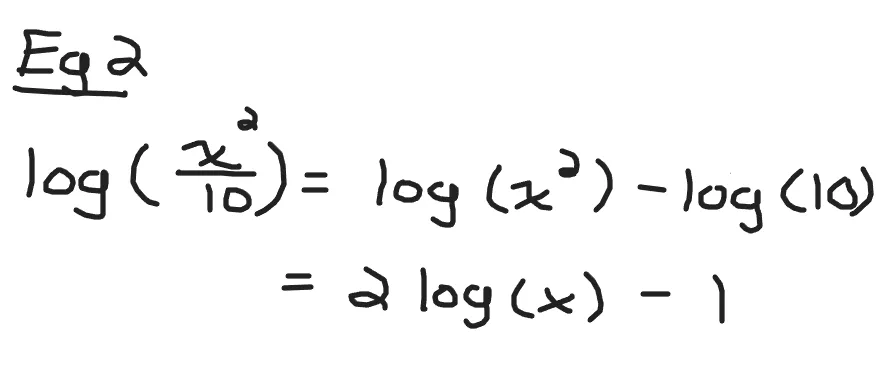
Example Three
Evaluate log(one hundred thousand).
One hundred thousand has five zeroes. This can be expressed as ten to the power of five. Use the power rule property where you can move the exponent of five in the logarithm input to the front of the logarithm. The answer is five.
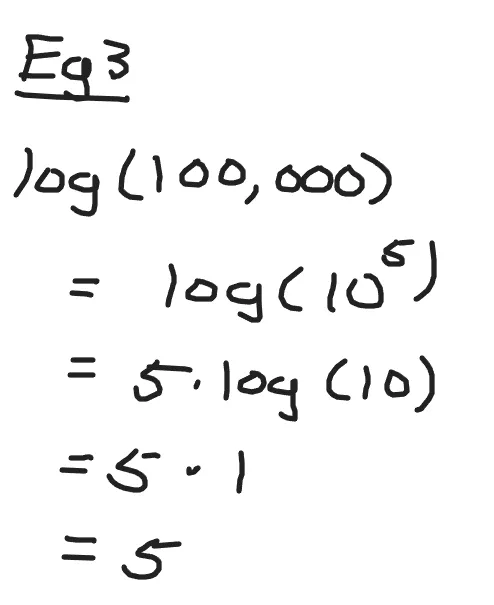
Example Four
Simplify log(100x2/y2)
This example involves a mixture of the quotient property and the product property. I use the quotient property first and then product property on log(100x^2).

