Hello there. In this math post, I cover the topic of evaluating logarithms.
Math text rendered with QuickLaTeX.com.
Contents
- Review Of Exponents
- What Is A Logarithm?
- Examples
- Practice Problems With Solutions
Review Of Exponents
Before getting into logarithms, I think it is a good idea to review exponents.
Instead of writing 7 x 7 x 7 x 7 x 7 where the seven appears five times, it is more compact and convienient to write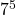 
instead. The number 7 is the number being multiplied and is called the base. The superscript or small number 5 represents how many times the seven appears and is called the exponent.
Negative Exponents
When it comes to negative exponents, make sure to not confuse this with multiplying with negative numbers. Having 8 to the power of negative two actually equates to 1 divided by 8 to the power of two.
Exponent Of One
The exponent of one case is just the number itself.
Zero Exponent
The zero exponent concept is difficult to explain. As long as the base number is non-zero or non-infinite, anything to the power of zero is one.
The best explanation of the zero exponent I can do is this with exponent laws:
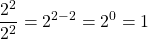
Zero exponent is like dividing by itself.
Fractional Exponents
Fractional Exponents are kind of weird. They involve whole number exponents and the n-th root. When n = 2 the n-th root becomes the well-known square root. Let's look at a few examples.
What Is A Logarithm?
Logarithms are used to solve for unknown exponents when we are given a base and an answer. The format for a logarithm is as follows:
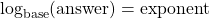
which corresponds to:
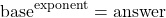
In many cases the default base for logarithms is 10.
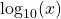
Another common base is the Euler's number of e being approximately 2.718. Instead of writing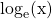 
, we write 
.
Sometimes you may see binary logarithms of base 2. It is written as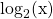 
.
Remember that logarithms are exponents.
Examples
Here are some examples to show how logarithms are evaluated.
Example One
What is the numeric value for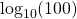 
.
Remember that when you evaluate logarithms you get an exponent. To evaluate this logarithm ask yourself 10 to the power of what exponent gives 100? In this case, the answer is 2.
Example Two - Negative Exponents
What is the numeric value for 
.
The base here is 2. You would ask yourself 2 to the power of what exponent is a quarter. Positive exponents do not work here as 2 to the power of a positive exponent gives a value greater than 2. For this case you would need a negative exponent answer. The answer here would be negative two as two the power of negative 2 is a quarter.
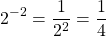
Example Three
Evaluate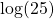 
(to 4 decimal places).
As no base subscript is given, you can assume a base of ten. With this question it is ideal to use a calculator to evaluate this exponent. Note that ten to the power of 1 gives 10 and ten to the power of 2 is 100. The answer to the logarithm will be somewhere between 1 and 2.
Using a calculator we have 
.
Practice Problems With Solutions
Evaluate the following logarithms. Assume base 10 if you see just log. For some of them you can use a calculator.
Solutions
3
-2
6 (There are six zeroes in one million.)
5
3 + 2 = 5
-2 + 3 = 1
Approximately 1.699.
