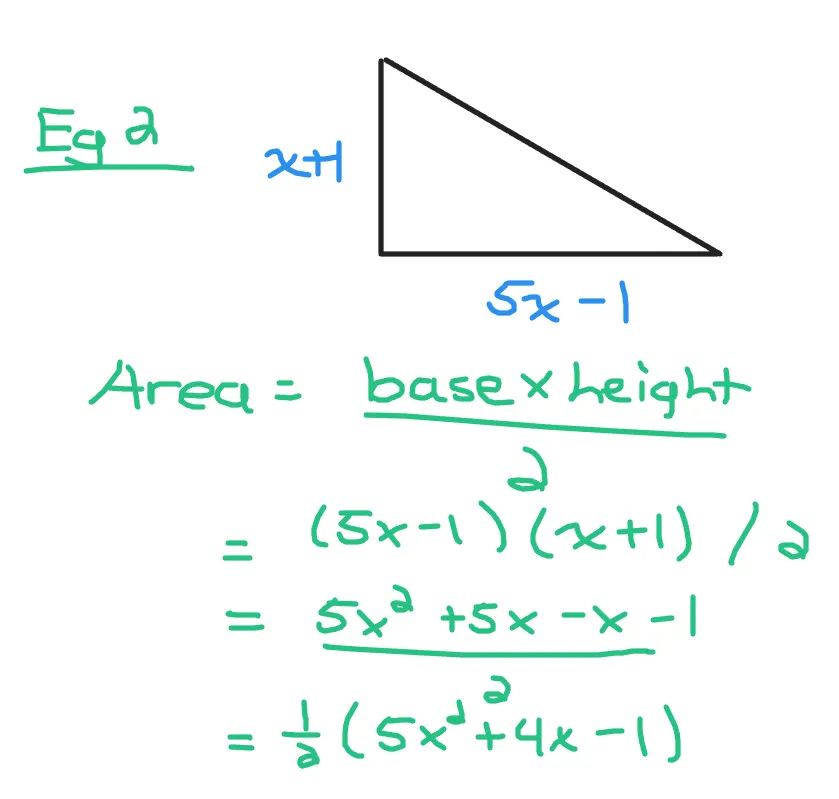Hi there. In this math post I cover multiplying binomials with the FOIL method. This is one of those topics with not many real life applications. Multiplying binomials is one of those math skills that is a part of the algebra toolbox. Think of it like learning to use the knife for cutting fish or something.
Topics
- Review Of Distributive Law
- FOIL Method For Multiplying Binomials
- Area Examples
Review Of Distributive Law
I think it is a good idea to review the distributive law before getting into multiplying binomials. Here are some examples of the distributive law.
Example One
Multiply 3(x + 7).
With the quantity we have a number on the left side of the bracket being multiplied by a binomial in the bracket. Recall that a binomial contains two terms that is separate by either a plus or minus sign.
For 3(x + 7), multiply the three with the x to obtain 3x. Multiplying three with seven gives a positive 21. The result should be 3x + 21. I have attached a screenshot with visuals and arrows.
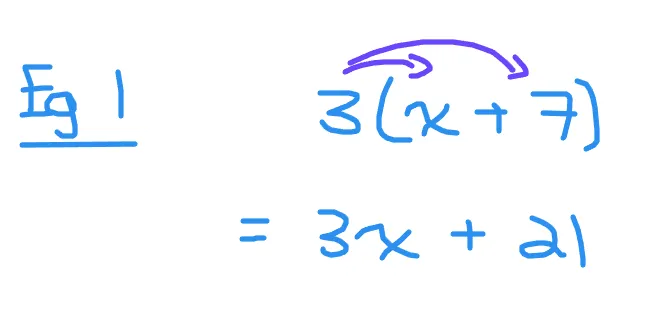
Example Two
Simplify -5(2x - 9).
Multiply the negative five with the 2x to obtain negative 10x. For the second term multiply negative five with negative nine to obtain positive 45. The resulting answer should be -10x + 45.
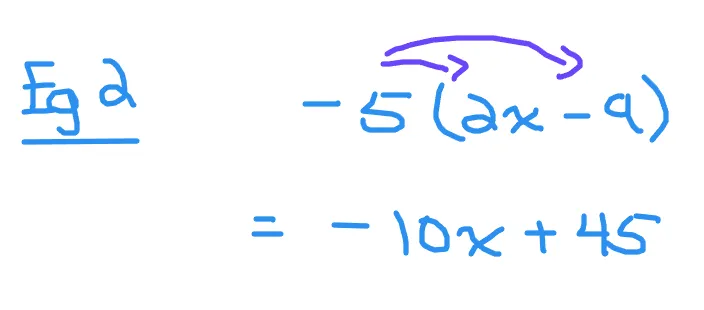
Example Three - Area Of Rectangle
The area of a rectangle is length multiplied by the width. Let the length of the rectangle be 10 units and the width be (2x - 1). What is the area of the rectangle?
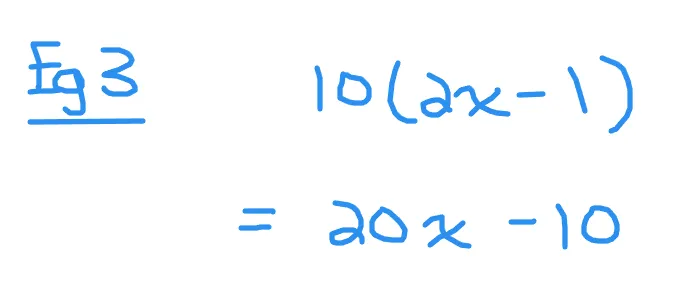
The algebraic expression is 10(2x - 1). Multiply the ten with 2x to obtain 20x. Next multiply the ten with negative one to obtain -10. The resulting area of this rectangle would be 20x - 10 square units.

FOIL Method For Multiplying Binomials
Multiplying binomials is a small extension of the distributive law. I like to think of it like doing the distributive law twice and then simplify like terms. Here are some examples.
Example One
Multiply (x + 1)(x + 2).
Start with the first terms from both binomials. That is multiply x with x to obtain x-squared. The second term involved the outer terms. Multiply the x from the left with the 2 from the right to obtain 2x.
Next is the inner part. Multiply 1 with the x from (x + 2). This yields x. The last terms are one and 2 being multiplied together to get 2.
The result is shown in the screenshot below. It is x^2 + 3x + 2 after simplification.

Example Two
What is the result of (2x + 1)(x - 3)?
The first part is 2x times x to get 2x^2. Multiplying 2x and negative three gives -6x for the outer part.
Inner would be one times x to get x and the last part is one times negative three to get negative three.
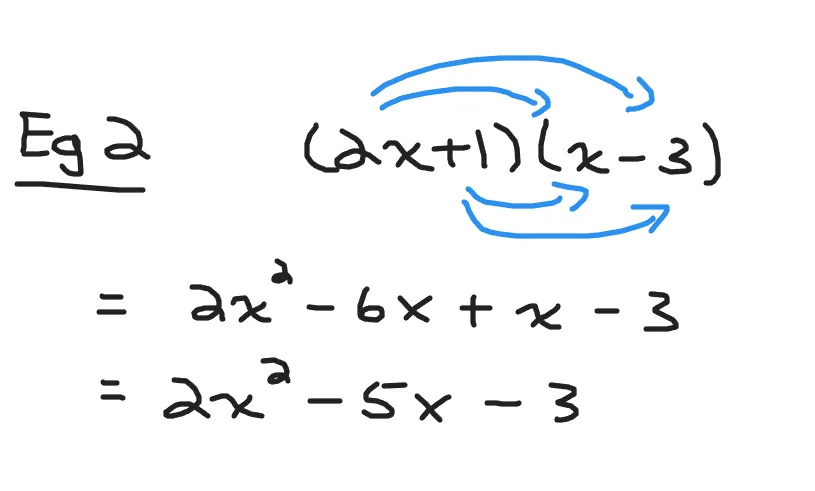
Example Three
Multiply (5x - 2)^2 = (5x - 2)(5x - 2).
With the example just be careful with the algebra and the negative signs. See the screenshot below for the steps.


Area Examples
One of the applications of multiplying binomials that I can think of is area of a rectangle. There are business profit examples but I do not really feature that here.
Area Example One
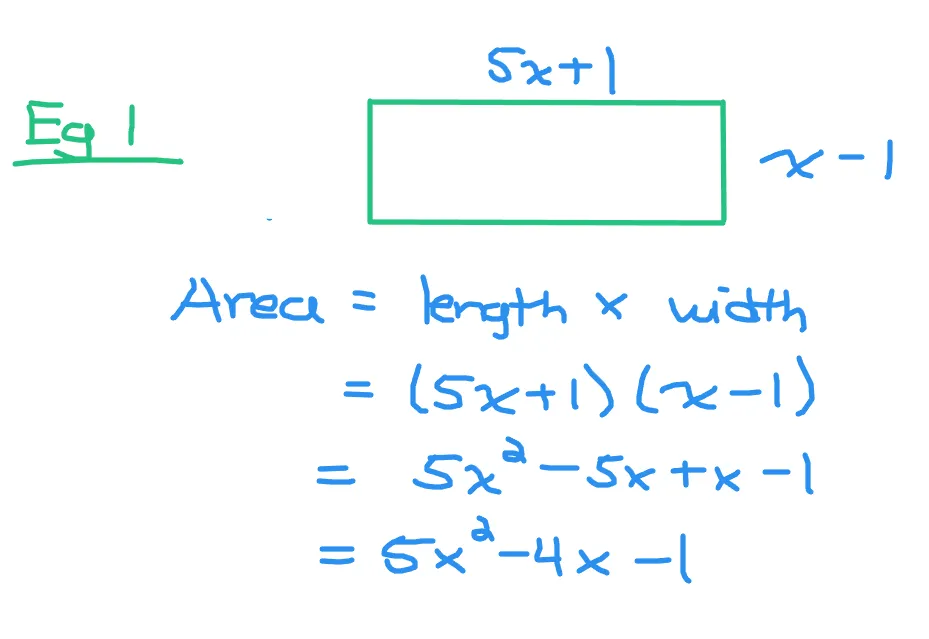
The length of a rectangle is (x + 1) and the width is (2x + 3) with centimetres as the unit. What is the area?
Multiply the two binomials together to obtain the area of the rectangle.
Area Example Two
A triangle has a base length of (5x - 1) and a height of (x + 1). What is the area of the triangle?
The area of the triangle is the base length multiplied by the height divided by two.