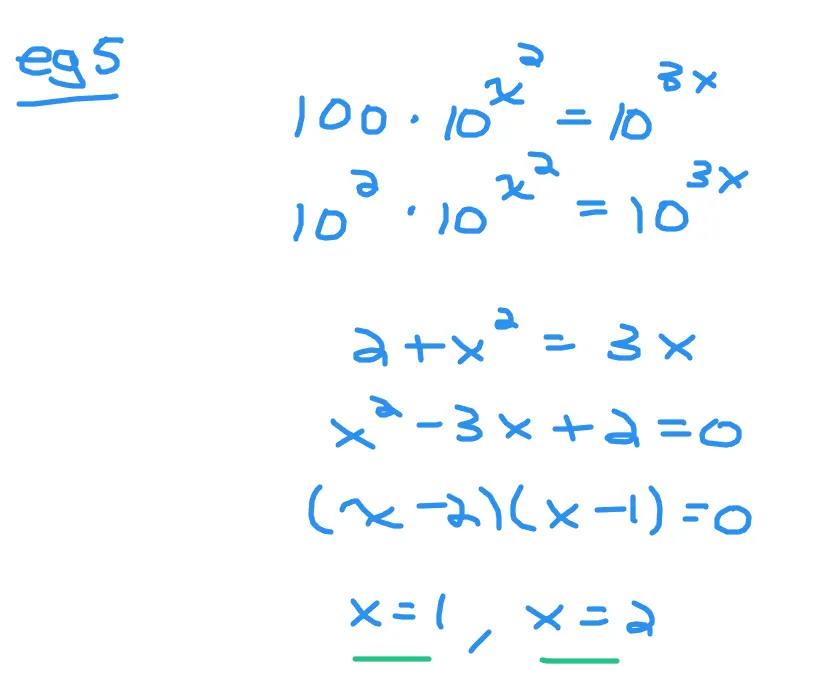Hi everyone. In this math guide, I cover the topic of solving exponential equations. It is assumed that the reader is familiar with exponents and has good number sense.

Topics
- Review Of Exponent Properties
- One Step Solving For Exponents Example
- Examples Of Solving Exponential Equations
Review Of Exponent Properties
Before getting into solving exponential equations, I would like to display some exponent properties. Note that I do not cover fractional exponents here.
Sum Of Exponents
As long as the base is the same and you have multiplication you can add the exponents together.

Difference Of Exponents
For the division case where the base is the same, subtract the top exponent with the bottom exponent.
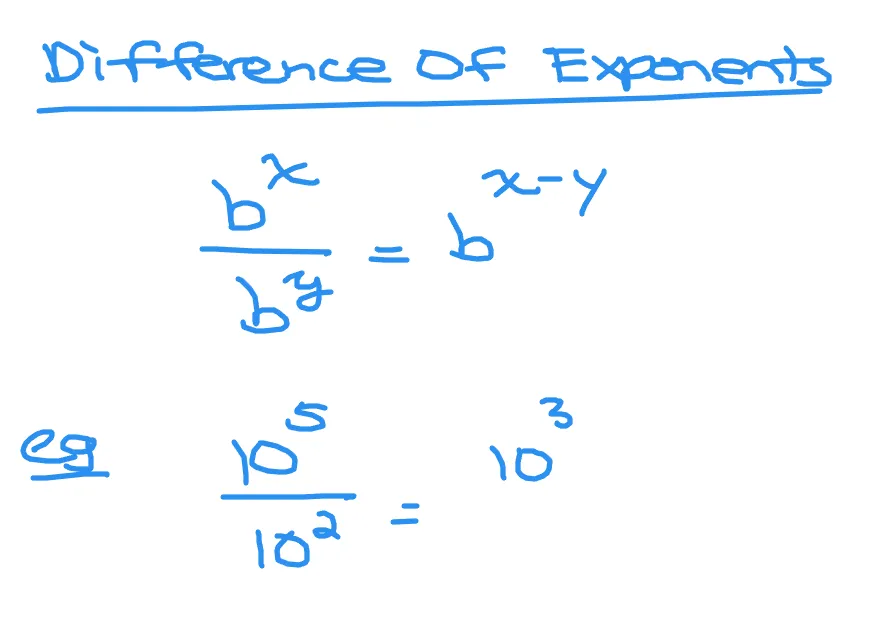
Exponents On Fractions
Exponents can be applied on fractions. A fraction with an exponent goes with the numerator and the denominator of the fraction.

Negative Exponents
When it comes to negative exponents remember that there are no negative signs added. A negative exponent involves a reciprocal where you flip the fraction and turn the negative exponent to a positive exponent.

Power To Power, Multiply Exponents
Multiplying exponents is valid when there is a single base to the power of the first exponent. This quantity also has a second exponent on the outside. See screenshot below for the algebra rule and example.
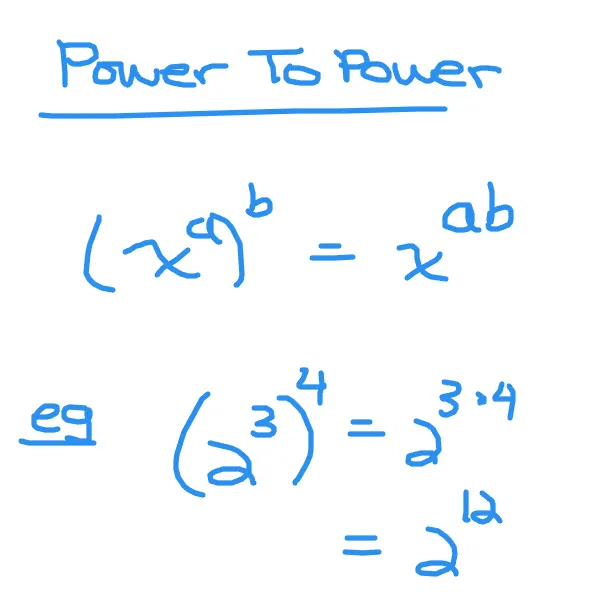
One Step Solving For Exponents Example
In this section I present simple examples of solving for exponents.
Example One
What is the value of x for 2^x = 8?
Think of this question as two to the power of what number is equal to 8? Two to the power of 1 is two, two to the power of 2 is 2 x 2 = 4. The answer here is 3 as two to the power of three is 2 x 2 x 2 = 3.
Example Two
What is the value of x for (1/3)^x = 9?
One third can be rewritten as three to the power of negative one. The left side then turns into three to the power of negative x. Nine on the right side can be rewritten as three to the power of 2. There is a common base of three. Solve for x in -x = 2 to obtain x = -2.
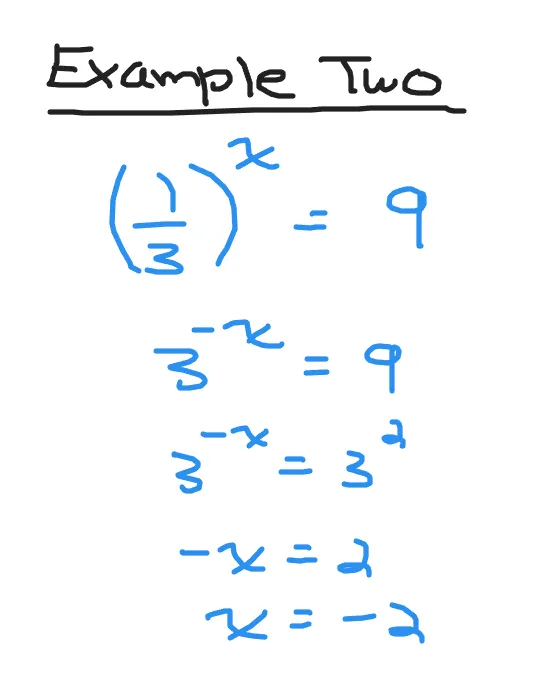
Example Three
What is the value of x for (2/5)^x = 8/125?
One way to look at this is to apply the distribute the variable x in the left side fraction. This yields 2^x / 5^x = 8 /125.
In the numerator two to the power of x gives 8. With the denominator five to the power of x gives 125. The answer here is x = 3 as two to the power of 3 gives eight as well as five to the power of three gives 125.
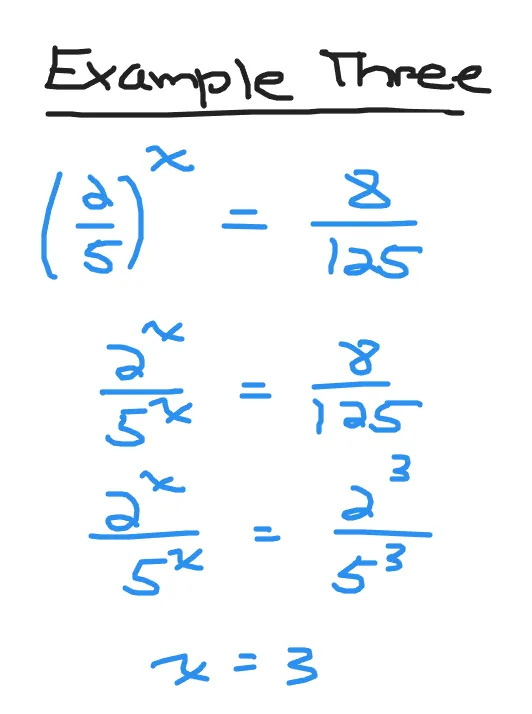
Examples Of Solving Exponential Equations
Screenshots are from witeboard.com with the use of my Wacom Tablet and stylus.
Example One
Solve for x in three to the power of (x + 2) equal to 27.
Rewrite 27 as three to the power of 3. The bases are now three. Solve for x in the exponents.
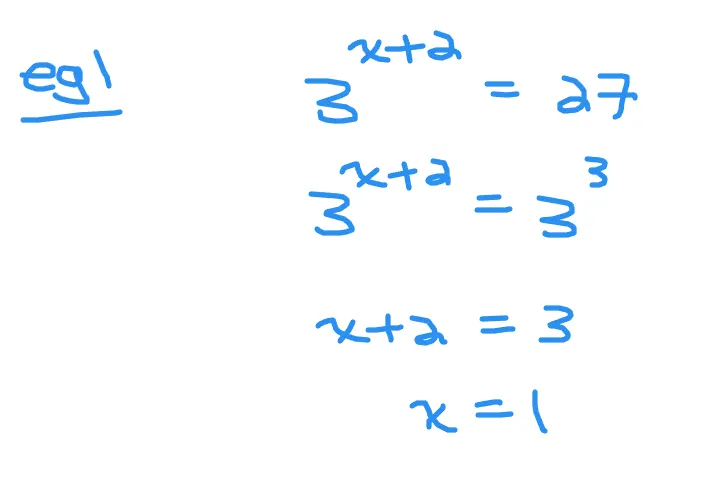
Example Two
What is the value of x in 8^(2x - 1) = 2?
Eight can be rewritten as two to the power of 3 with the exponent of 2x - 1. You have an exponent exposed to another exponent. Multiply the 3 and (2x - 1) with the use of the distributive law. The new exponent on the left would be 6x - 3. Two on the right is two to the power of one.
As there is a common base of two, equate the exponents and solve for x.
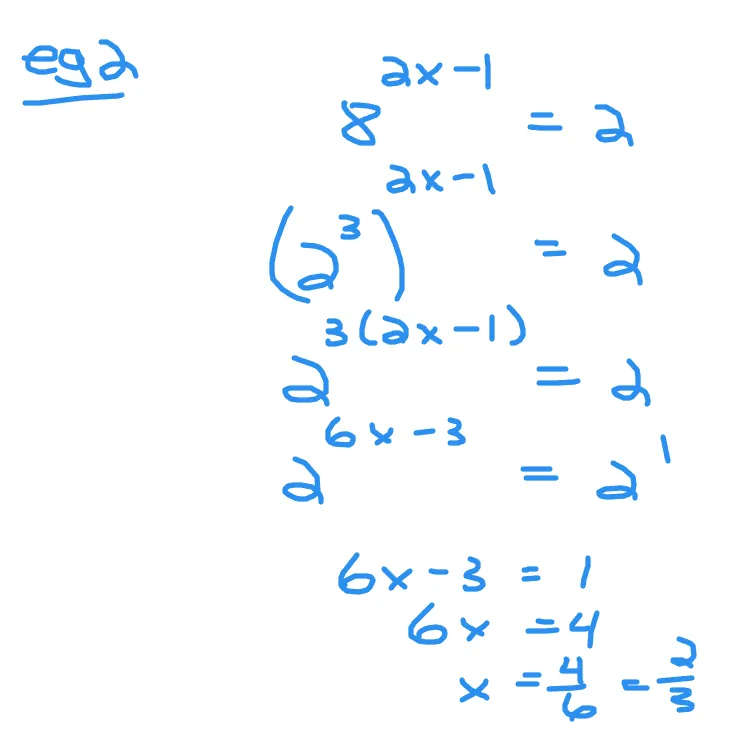
Example Three
Determine the value of x in 4 * 2^(5x + 7) = 16.
The four is not with the exponent of 5x + 7. You can divide both sides by four. This removes the four on the left and the right side is four from sixteen divided by four.
Rewrite the four on the right as two to the power of two. Equate the exponents and solve the linear equation for x.
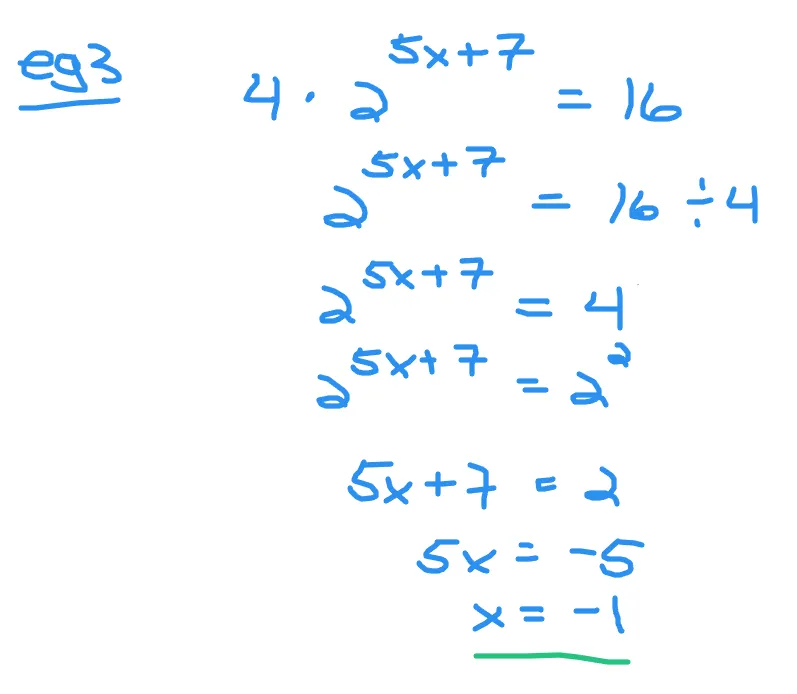
Example Four - Use Factoring
In 2^(x + 1) + 2^(x) = 3 what is the value of x?
This question looks kind of scary. The right side is a three which cannot really be written with base two with a whole number exponent. For this one, common factor out a 2^x on the left side. Note that 2^(x + 1) is equal to 2 * 2^x.
You should get a three as a factor along with the factor of 2^x. Divide both sides by three to obtain 2^x = 1. The value of x here is zero that satisfies the equation.

Example Five - Solve Quadratic Equation In Exponents
What are the values of x that satisfy 100*10^(x^2) = 10^(3x)?
Rewrite one hundred as ten to the power of two. There is a common base of ten. Equate the exponents to obtain the equation of 2 + x^2 = 3x. With this quadratic equation start with moving all the terms to the left side with the right side equal to zero.
Factor the left side of the quadratic equation of x^2 - 3x + 2 = 0 Which two numbers multiply to positive two and the same two numbers add up to negative three? That would be -2 and -1. The factored form would be (x - 2)(x -1). The solutions for x would be x = 1 and x = 2.