Сангаку №1
Кілька років тому я познайомився з Euclidea, і розв'язуючи там задачі головоломки я пригадував свій 7 клас, задачі на побудову. Правда клас мій тоді був шостим, бо вчилися ми 10 років, не те що зараз аж 12. Та граючись з Euclidea мені хотілося б в ній бачити вільний конструктор для побудови своїх малюнків до задач, а не лише розв'язування вже готових... - пізніше я знайшов Geogebra.
Раз вже я в минулому пості показав картинку, то розкажу про саму цю задачу.
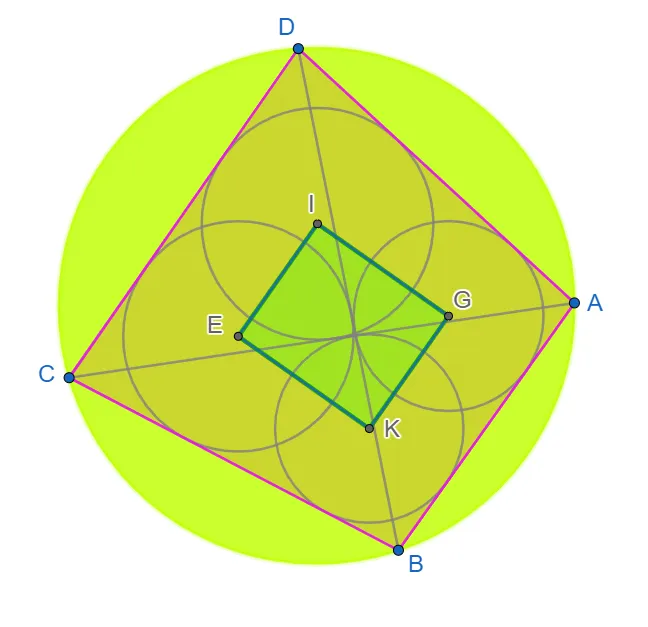
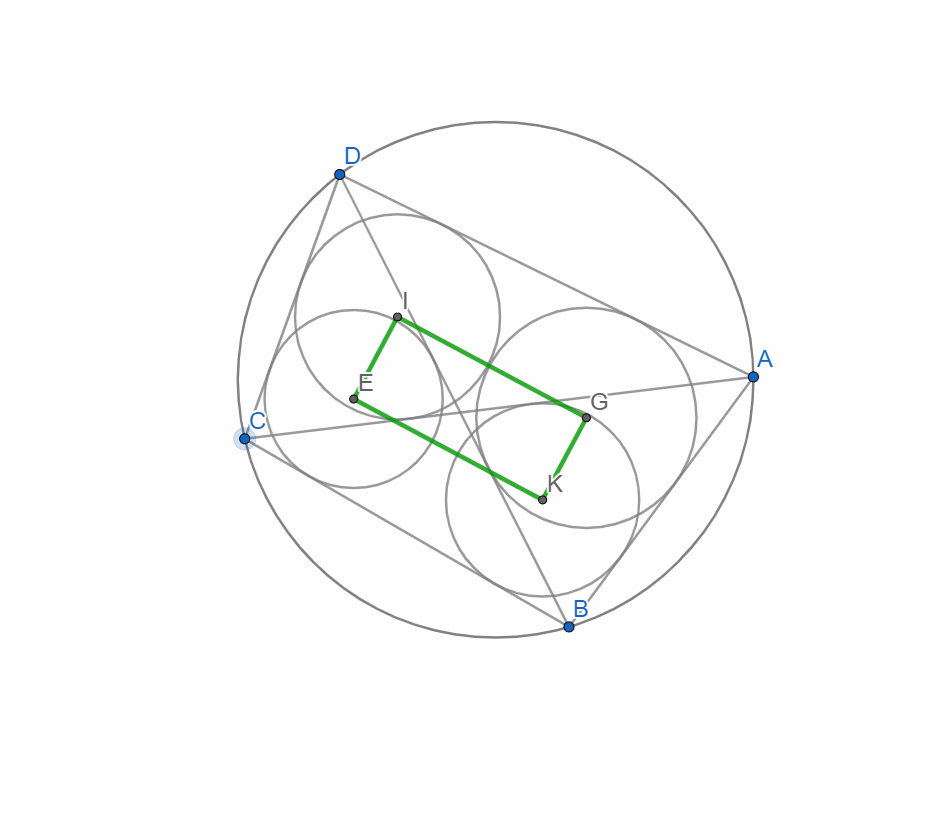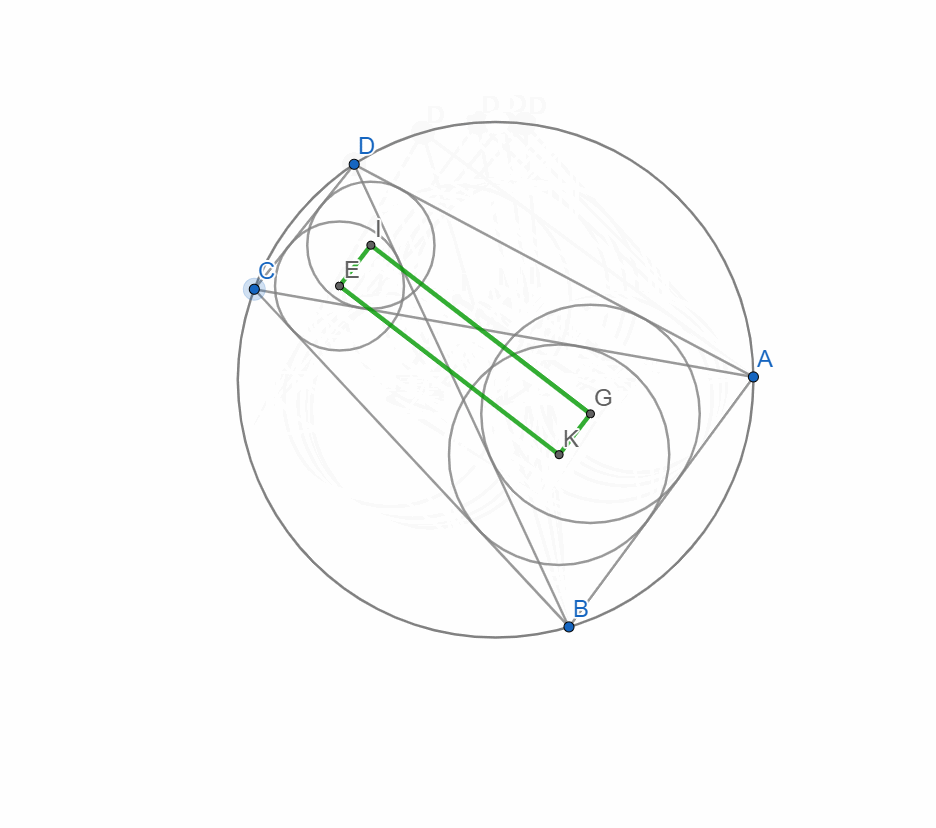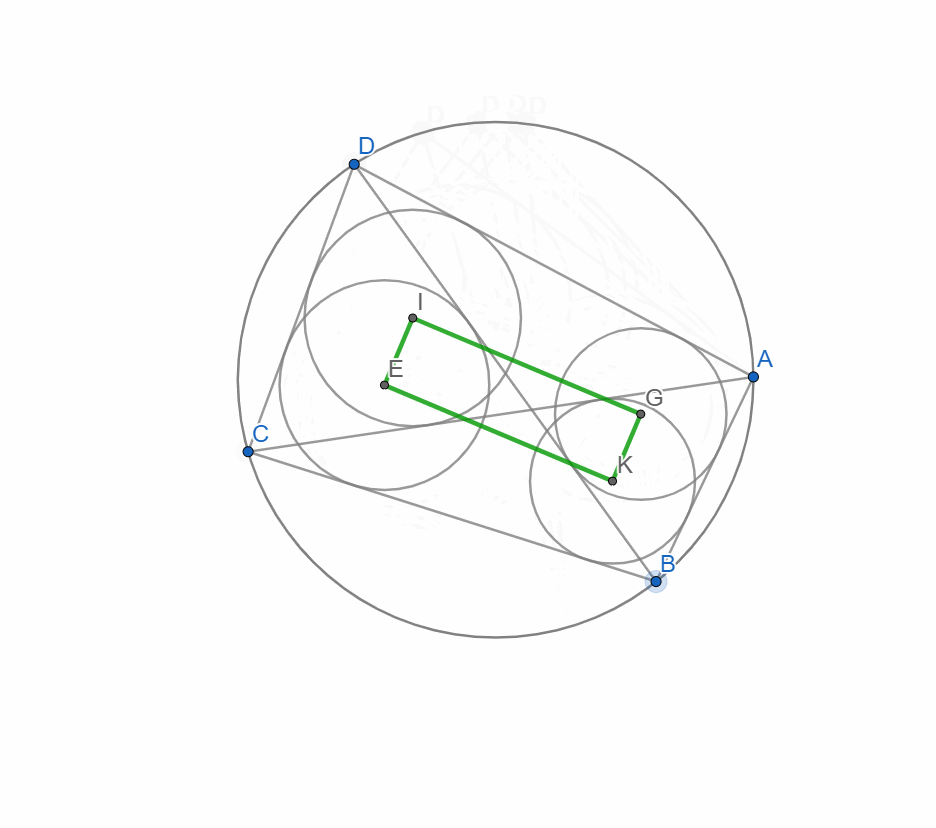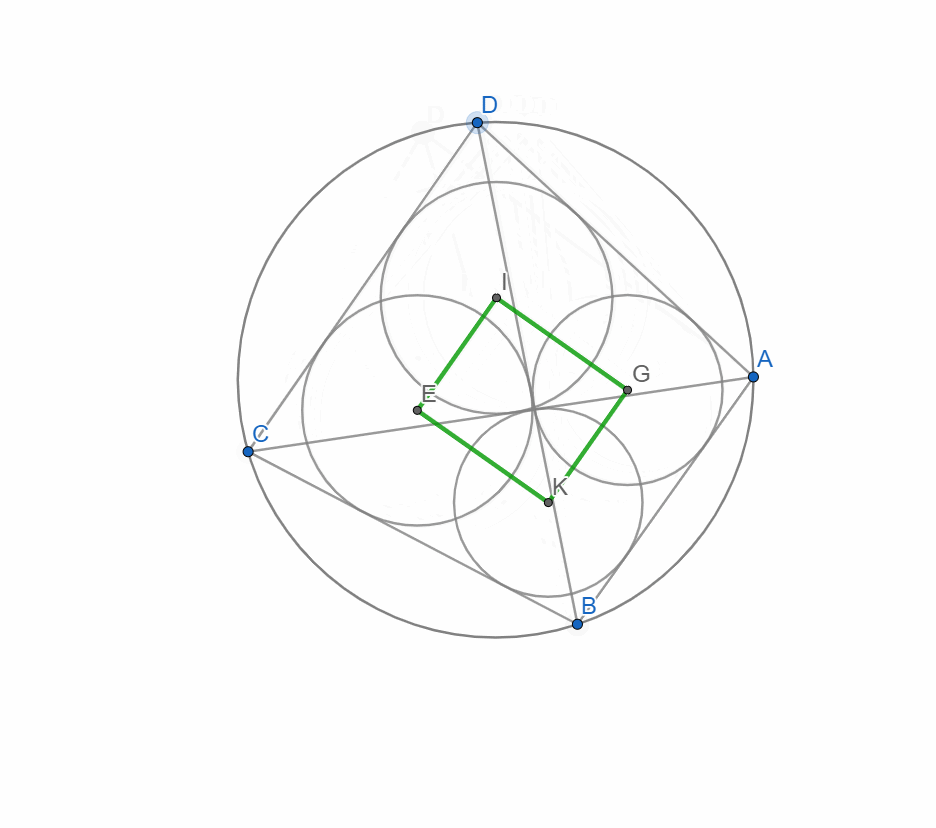
В коло вписано чотирикутник. Дві діагоналі розбивають цей чотирикутник на чотири трикутники в кожне з яких вписано коло. І виходить так що центри цих кіл утворюють прямокутник. І тут можна сформулювати не одну задачу. Можна просто побудувати, можна довести це дійсно прямокутник, можна познаходити розміри цього прямокутника, радіуси(центри) кіл...
Зараз я просто покажу як я це будував у Geogebra.
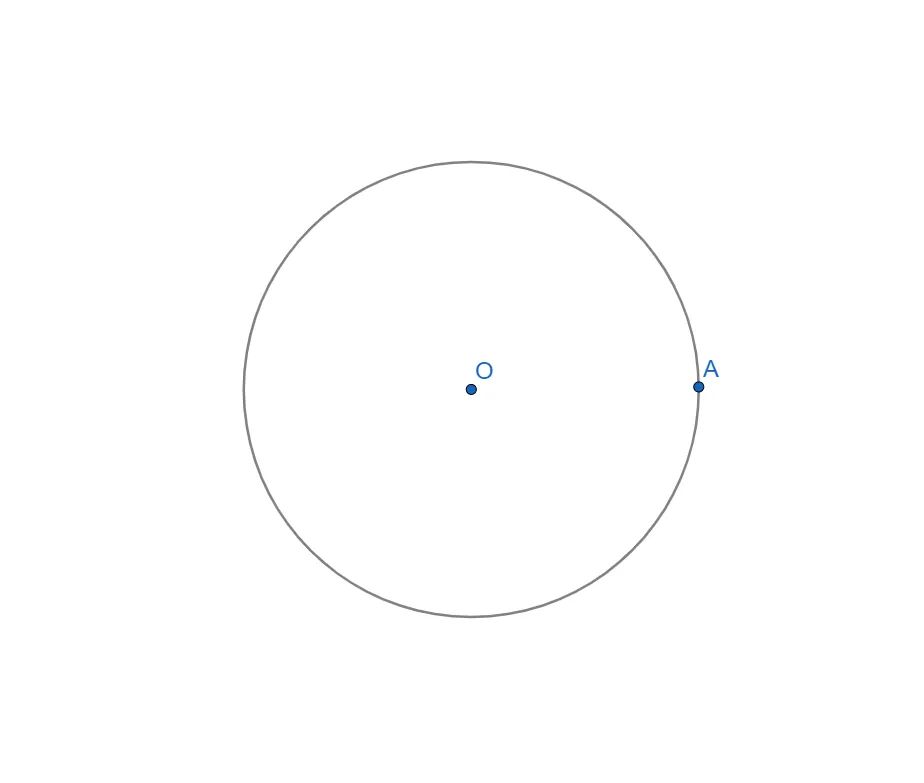
- Будуємо коло OA
Ставимо ще три точки - вершини чотирикутника вписаного в коло B,C,D.
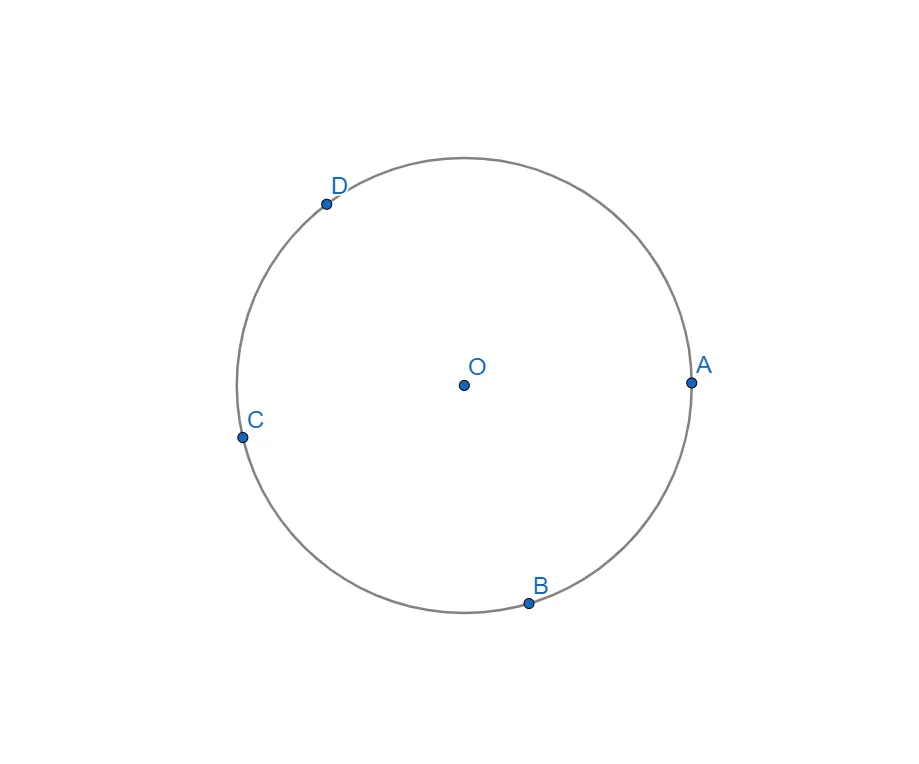
- З'єднуємо ці точки відрізками, утвориться чотирикутник ABCD.
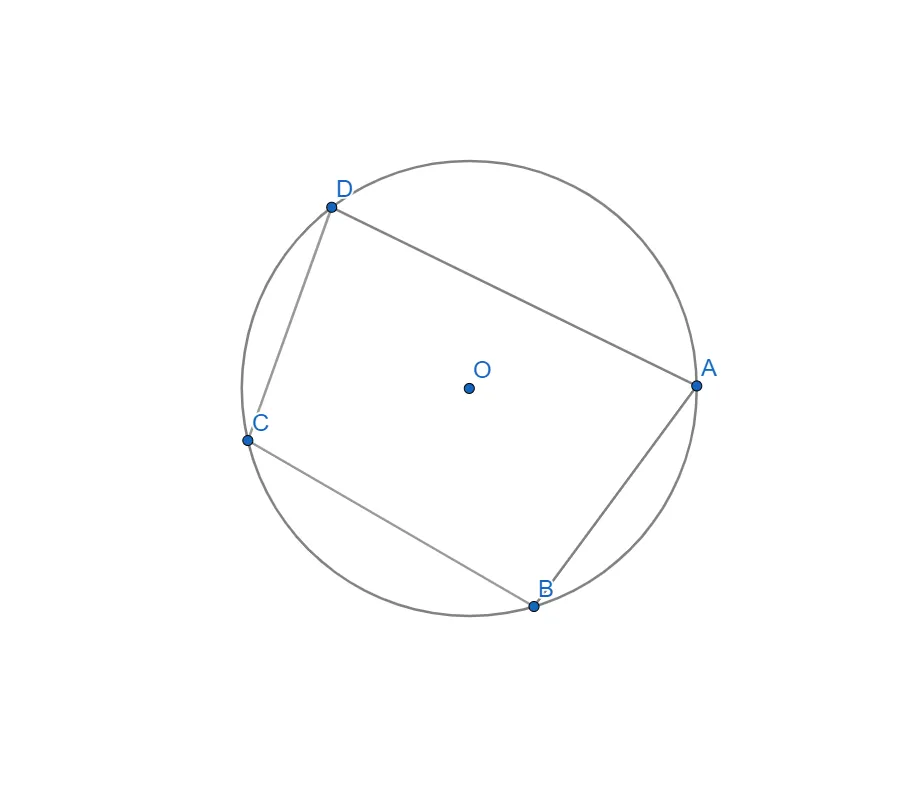
Проводимо діагоналі AC та BD.
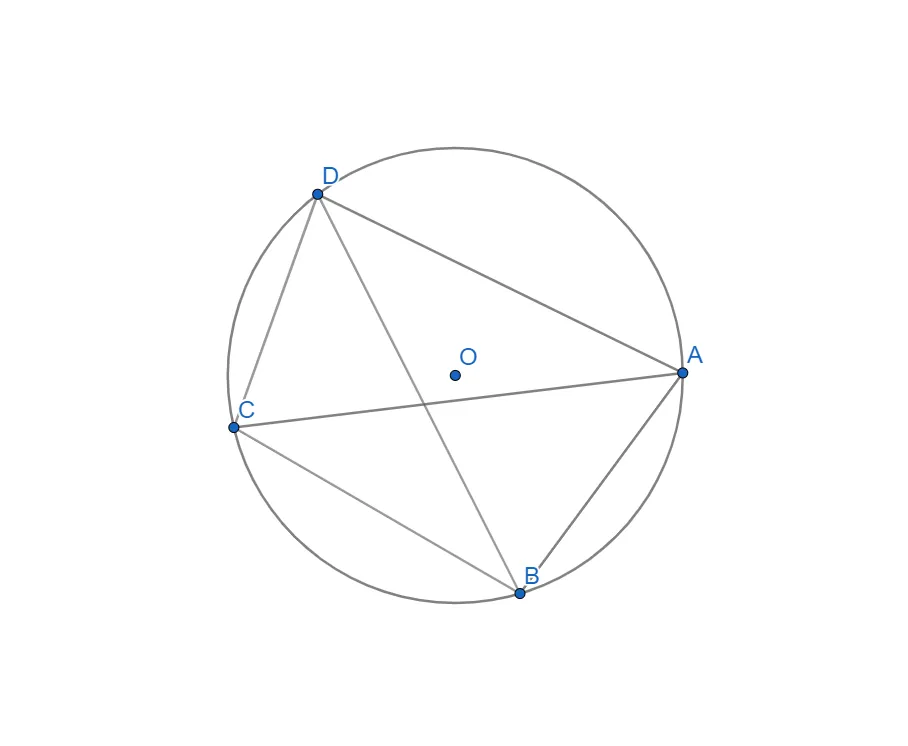
Вписуємо коло в трикутник CDB. Для цього знаходимо точку E - точку перетину бісектрис кутів CDB та DCB.
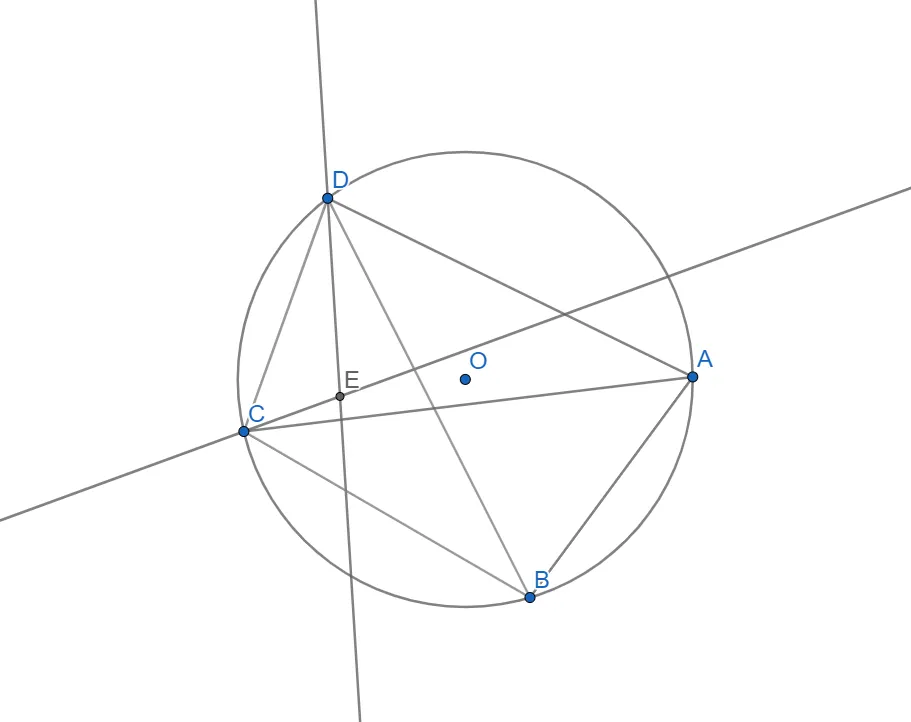
Знайдемо радіус - опустимо перпендикуляр EF зі знайденого центра E на будь-яку сторону трикутника CDB, наприклад CB.
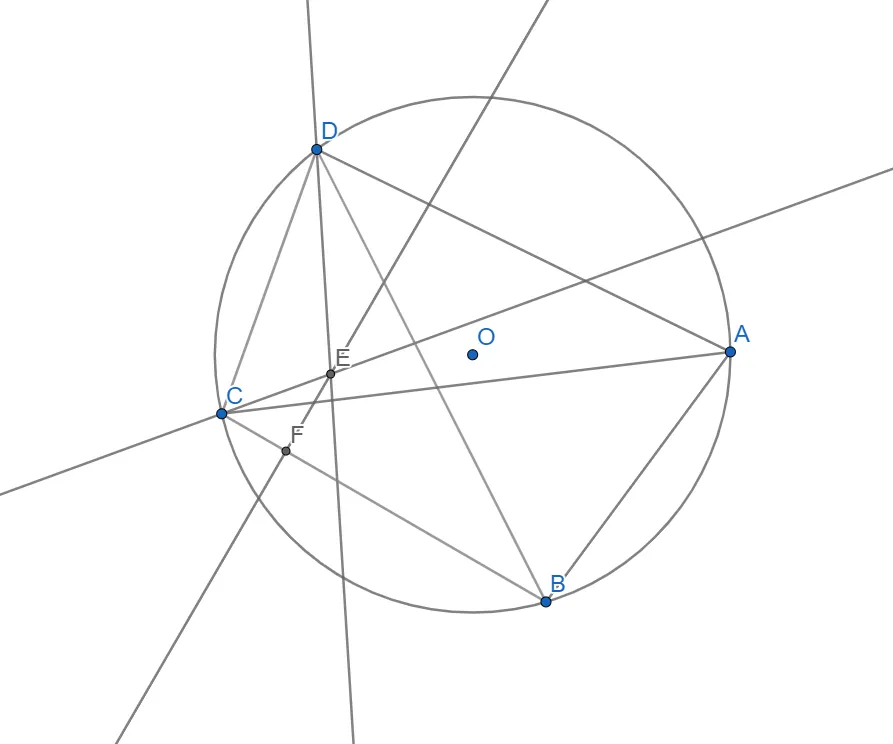
- Будуємо коло радіуса EF з центром в E.
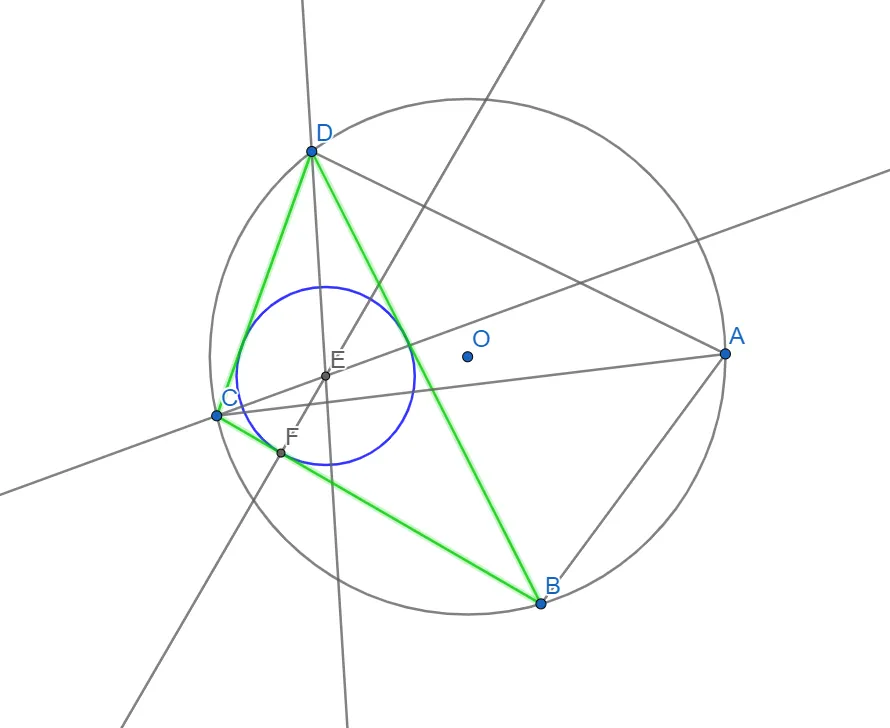
Аналогічно вписуємо коло в трикутник ABD.
Знаходимо точку перетину бісектрис кутів ADB і DAB - точку G(центр кола вписаного в трикутник DAB).
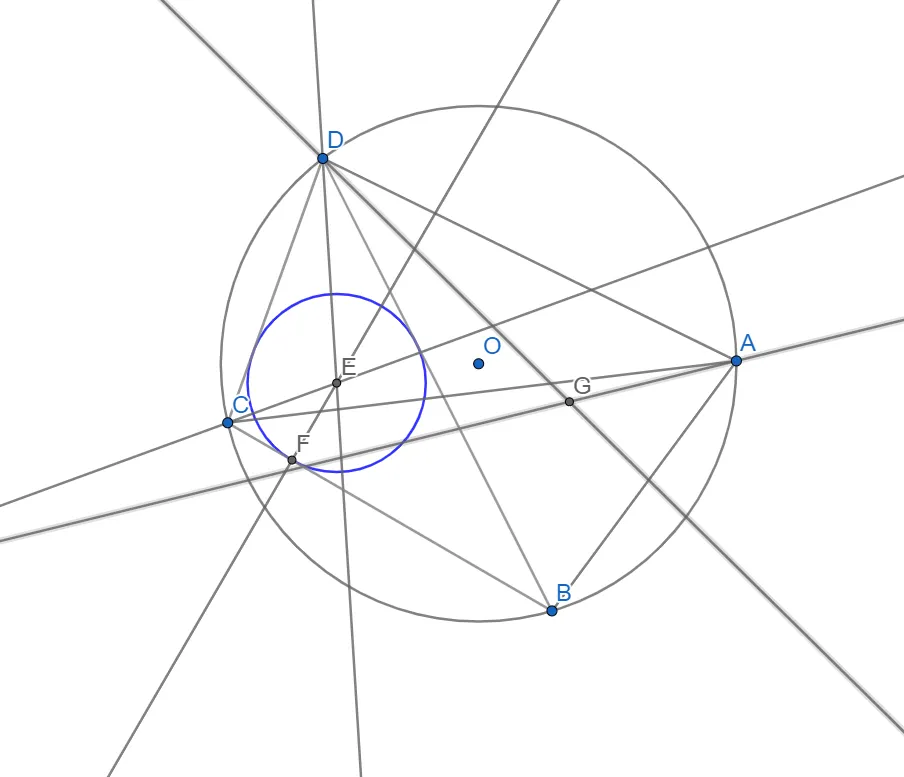
Опускаємо перпендикуляр GH на сторону DA.
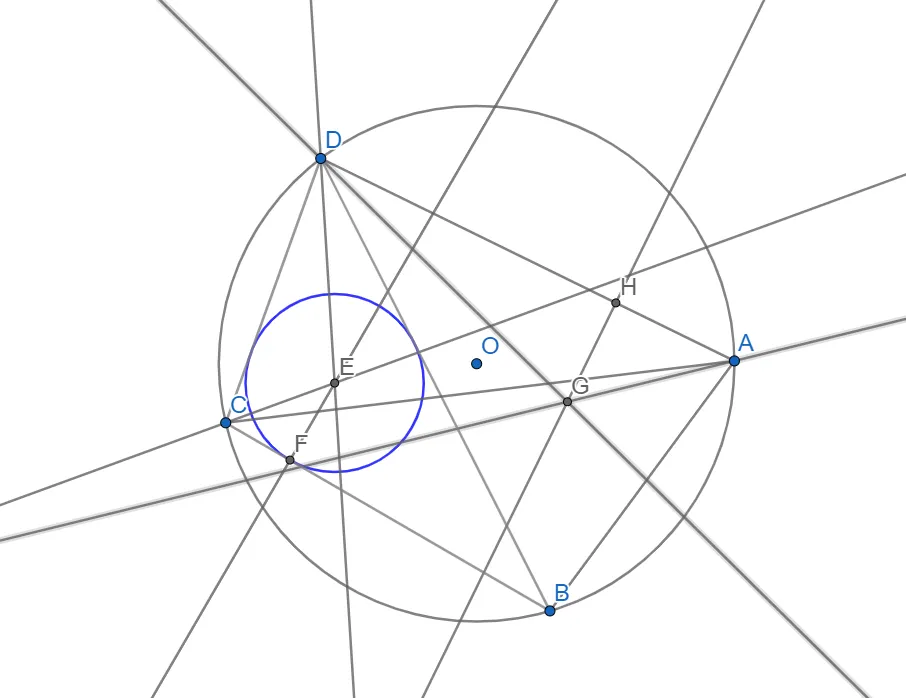
Будуємо коло з центром в точці G та радіусом ПР, вписане в трикутник DAB.
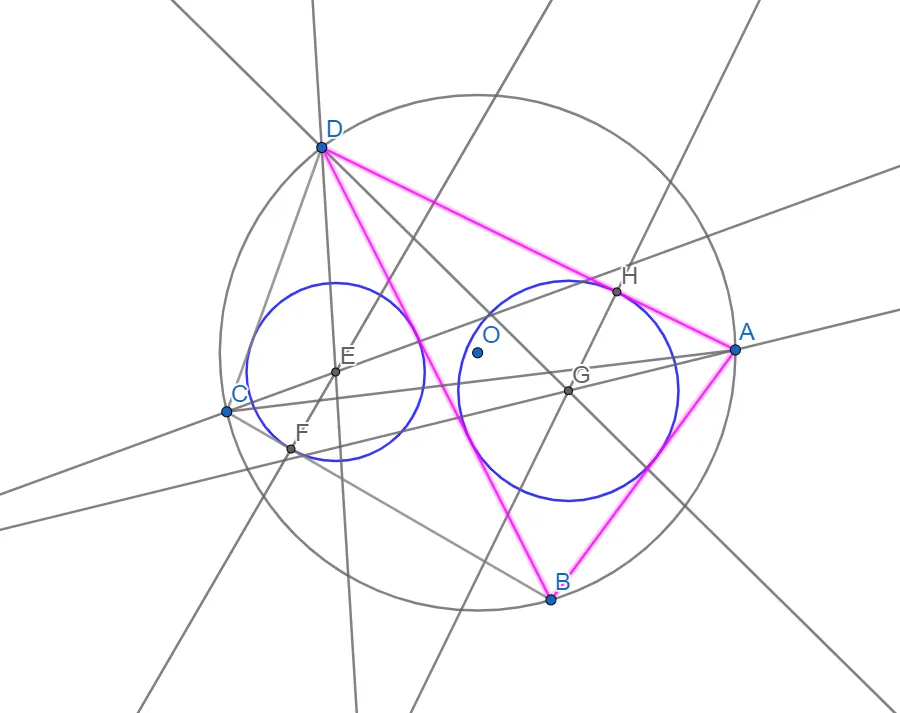
Відповідно іншій діагоналі CA будуємо ще два вписаних кола.
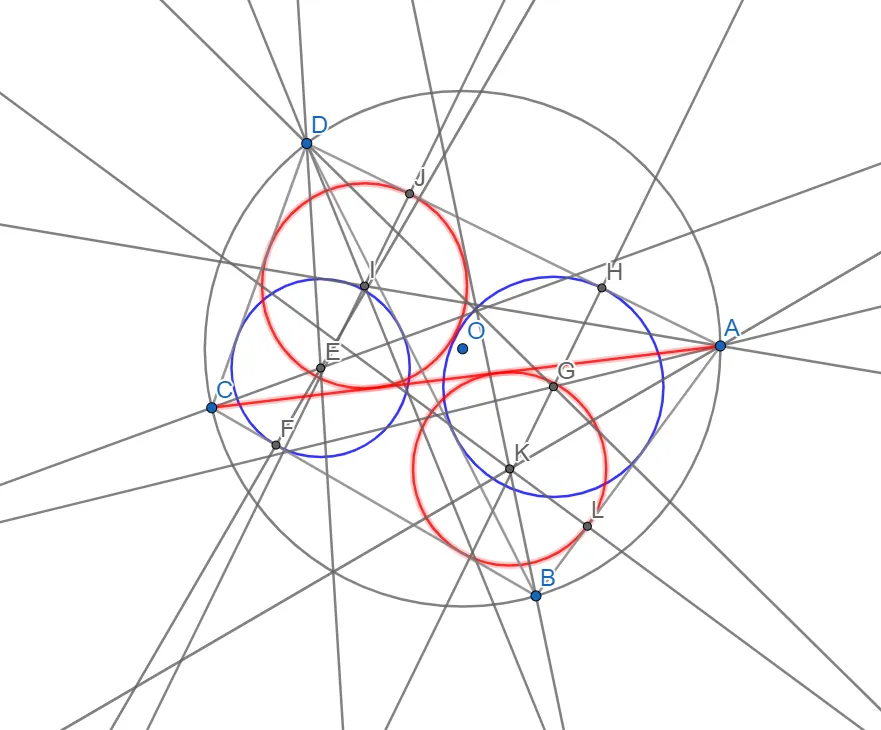
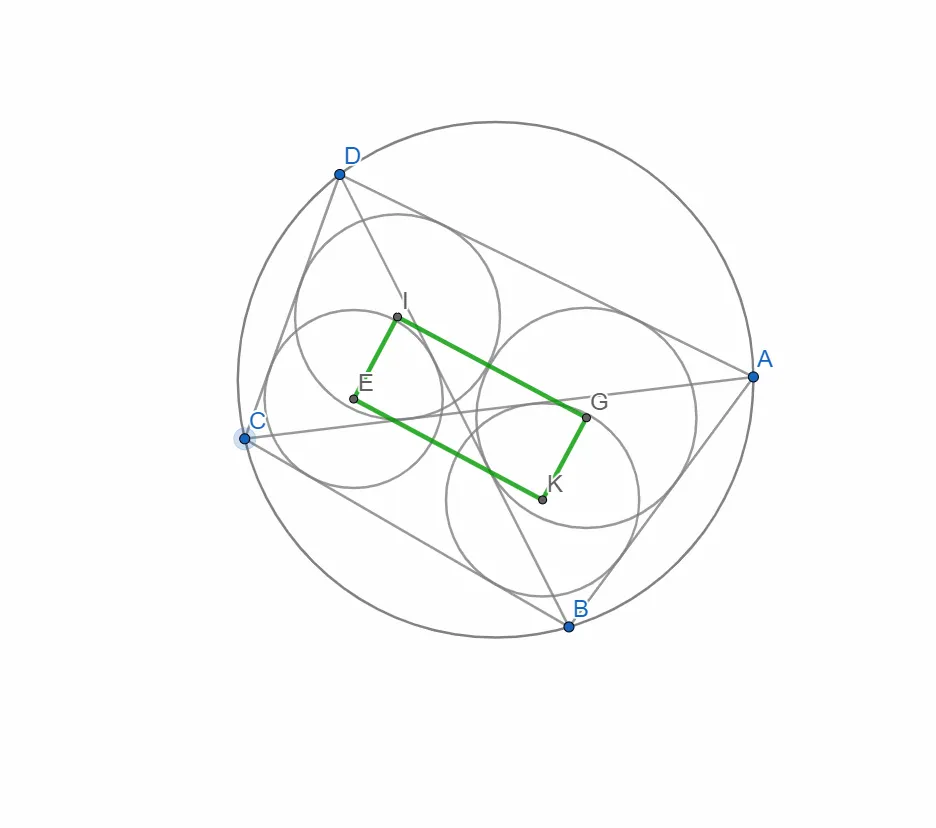
- Приберемо допоміжні елементи(бісектриси, серединні перпендикуляри)
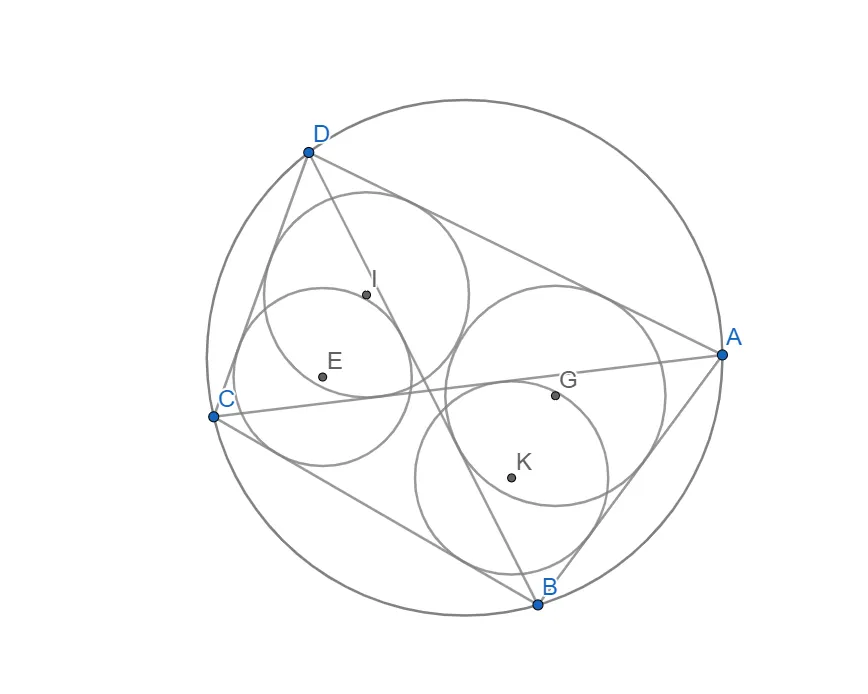
і побудуємо чотирикутник з вершинами у центрах кіл вписаних в трикутники утворених діагоналями чотирикутника.
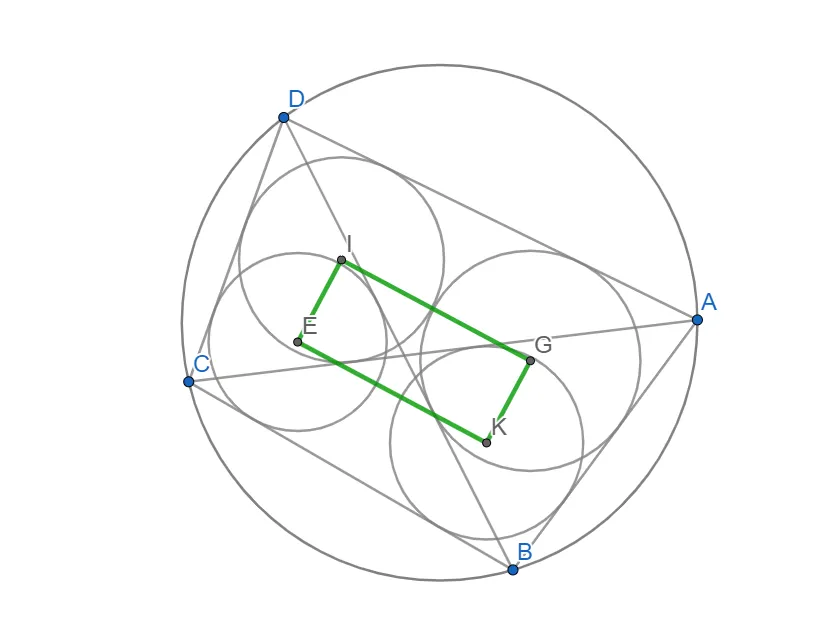
Переміщуючи вершини чотирикутника бачимо що чотирикутник утворений центрами кіл що вписані в трикутники утворені діагоналями і сторонами цього чотирикутника є(схожий) на прямокутник. Ну те що він справді прямокутник ще треба довести)) Але це вже інша
історіязадача. Над доведенням цього я ще не думав, проте задумався над ютуб-роликом таких побудов.
Ну і розфарбувати задля
красище більшої краси)))