Greetings, fellow sentient beings!
It might not be long before I'll have to solve the scaling problems concerning my own business initiatives, the board game project for which I made the @thewesternshores account among them. You know how important scaling is in relation to the blockchain...to any blockchain, too. But here I am going to theorize a little bit more in terms of logistics since that is one example for a problem that I would really have to solve or let others solve for me, and since it's pretty important in general, and because it's...well...nice to demonstrate.
It was only recently that I learned enough about some of the problems that Sun Tzu described about 2 500 years ago in The Art Of War related to supplying the army. We might all have though of it to some degree but the sheer scale of what was described caught me off guard. But they were also, in my opinion, put there to demonstrate an aspect rather than help people calculate with precision.
Since the precise numbers would vary greatly and in not a linear way when applying that knowledge to different scales.
All right, what he wrote was approximately...
To provide 1 (insert a small-scale unit) of grain to the army 1 000 Li away from home, you need 20 (the same small-scale unit) of grain.
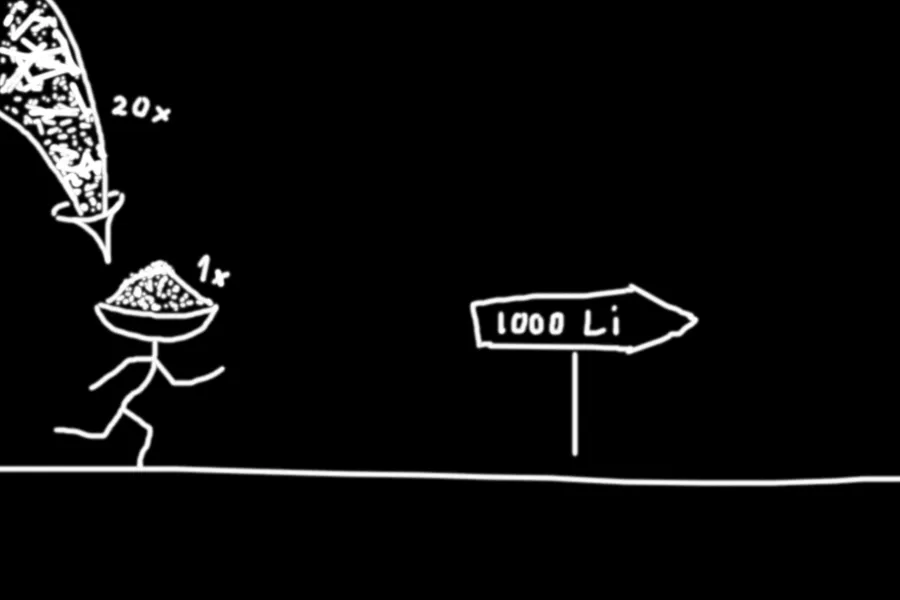
That distance equals about 500 kilometers which might be the whole width of my country but relatively short for the vast scale of China, even in its ancient state.
Anyway.
Basically, you need to feed/fuel the supply team and in ancient times transport was...that hard.
Those 20 units were more like virtual currency measuring everything that was needed, such as even maintenance of the cart that would drag the grain along with the army, payment, etc. You need to take into account all factors before you make your pricing.
(And I had not done so in my own business as it were up until recently. Lots of friction. And, most importantly, no chance of scaling for as long as it was only me employed with what I did. Still do.)
Back to the dude. Sun Tzu just pointed out how inefficient transporting grain from your own provinces is. Of course, you'd better feed your soldiers with your enemies' supplies.
Imagine though, your home-grown grain is the very product you need to shill.
Was it calculated for 1 unit only or for the whole container dragged which was standard?
Would the cost remain the same for a slightly larger container that needed the same crew?
Obviously, if the same amount of fuel could carry a heavier freight with the same risk and same need of maintenance, that would be a profit.
Would it be twice that for 2 000 Li?
Or would it be half that for 500 Li?
Would 2 or 3 ox teams require the double and triple the crew to take care of them?
Would a horse do better job than an ox or vice versa?
In general, we can say that transport is much more efficient today but scaling and cutting costs still matters so we're often looking for new and better solutions.
For now, I'll be working with scale only.
Brainstorming for solutions based on scale.
Make your grains smaller. Would they be enough that way?
Peel them beforehand. Wait...that could reduce durability. Is that my problem?
Try to send more and in bigger containers to the same destination or along the same route.
Optimize the power needed to drag the containers by...reducing administration. I.e., the people needed to overlook the operation. When expanding, you need more administration but making it scale properly means you need to provide each person with the optimal task that person can handle. If one person can handle 2 animals, don't upscale to 3 animals. Upscale to 4 animals so that the full capacity of the second person needed is fully used. Same as filling containers to the top.
In terms of board game packs instead of grain, I might want to make smaller packages, print the full capacity of the printing station, fill a whole ship with the boxes...that is increasing the scale in order to not waste space/power/opportunity...And then the market turns out to be of entirely different persuasion when it comes to the scale of what it wants...
That's another topic entirely.
I guess I just wanted to point out again that these calculations do not have to scale in a linear way.
There are groupings that can be made and there are cases you pay relatively the same for 1, or 2, or 3, or 4, so better pay 4. Then you pay relatively the same for 5, or 6, or 7, or 8, so better pay 8. Etc. But be sure that you need all 8 that you pay for. Otherwise, you get into trouble with the next concept which would be...
Storage.
Yours,
Manol