AMM Pools

Liquidity pools are a core component of decentralized finance (DeFi), enabling trading on decentralized exchanges (DEXs) like Uniswap or SushiSwap. They’re essentially pools of funds, where users (liquidity providers) deposit pairs of cryptocurrencies (e.g., ETH/USDT) to facilitate trading. We, at Splinterlands, are no stranger to Liquidity Pools (LP from now on). DEXs use an Automated Market Maker (AMM) model, where prices are determined by a mathematical formula, typically the constant product formula:

x * y = k

Here, x and y are the quantities of the two tokens, and k s a constant.

The relationship between the two tokens can be visualized by a Constant Product Curve.

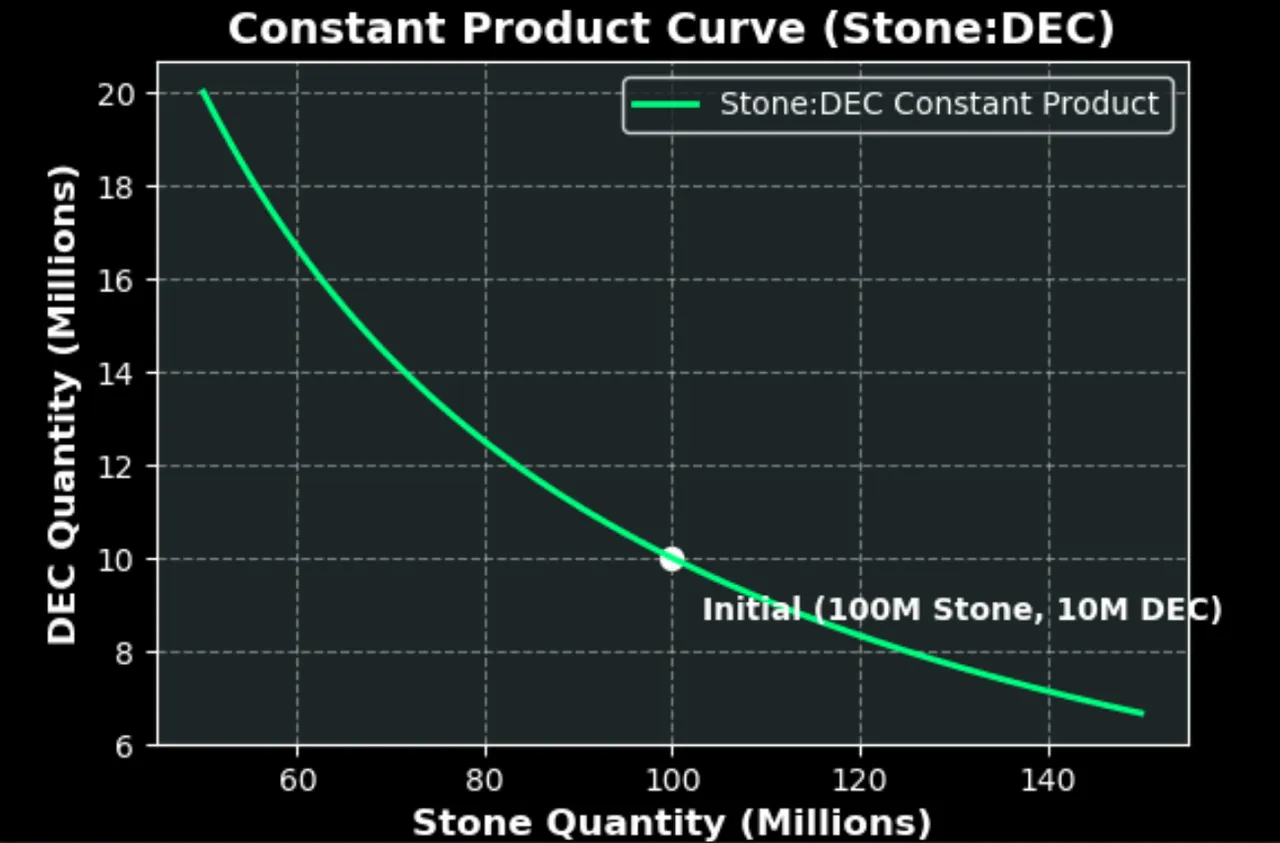
We are going to use the in-game product Stone:DEC pool to understand the details of an AMM pool. Today the price of Stone is:

1 Stone = 0.1 DEC

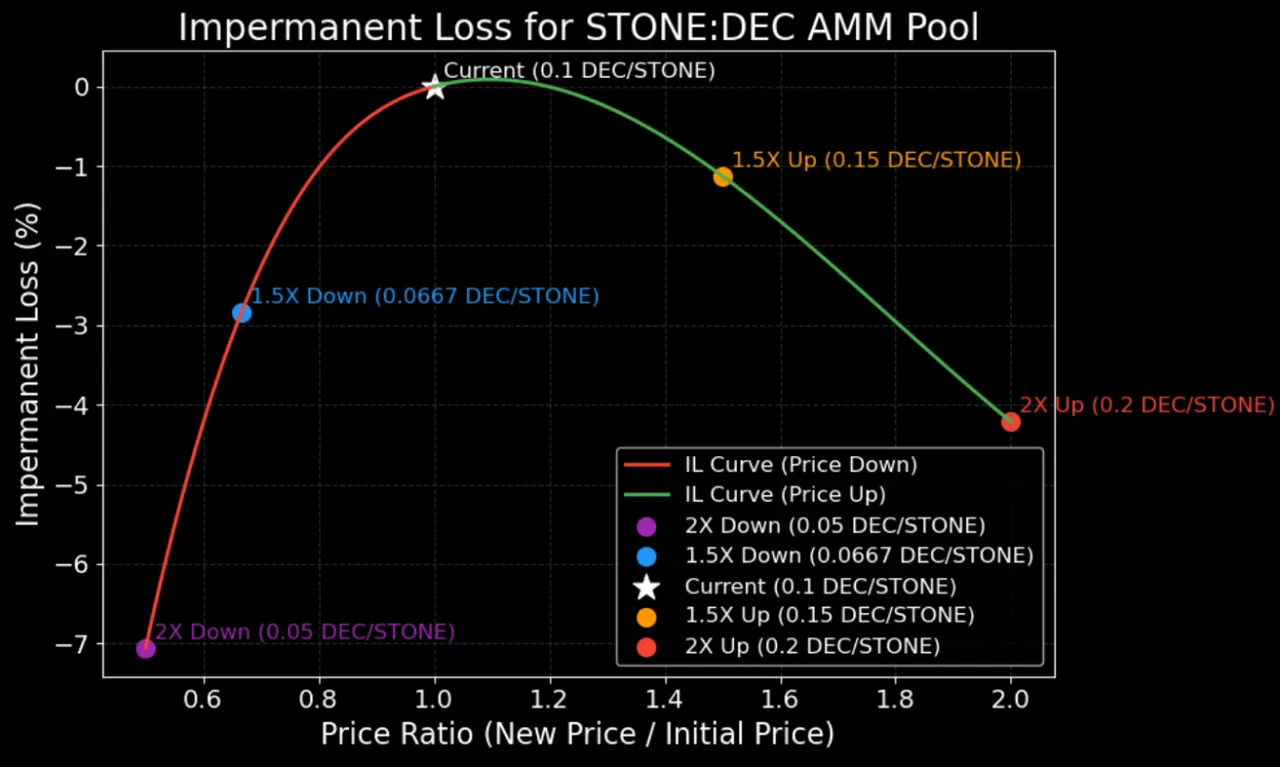
We can use this price to create an imaginary AMM constant product pool. The green curve here signifies the constant product curve or k. We can assume a scenario so that no new resource is added or subtracted to the pool, but doe to supply-demand (read new in-game features) price of the stone increases or decreases. We also assume that DEC is mostly at peg or near peg at 1000 DEC = $1. With these assumption in place we can investigate the scenarios where Stone goes up or down a lot say 2X!

In these scenarios shown on the plot, the size of ones share the pool remains the same. Due to the change of price, the pool automatically sells Stone for DEC if price of stone goes up. So the pool has more DEC than initial position. It does the opposite if price of stone goes down. Same thing happens to every stakeholders in the LP who owns proportional share.

Impermanent Loss

Impermanent Loss (IL) is the potential loss in value experienced by liquidity providers (LPs) in an Automated Market Maker (AMM) liquidity pool, such as the Stone:DEC pool, when the price of the pooled tokens diverges from their initial price ratio at the time of deposit, compared to simply holding the tokens outside the pool. It occurs because AMMs, using a constant product formula (x * y = k ), automatically rebalance the pool’s token quantities as prices change, causing LPs to hold more of the depreciating token and less of the appreciating one.

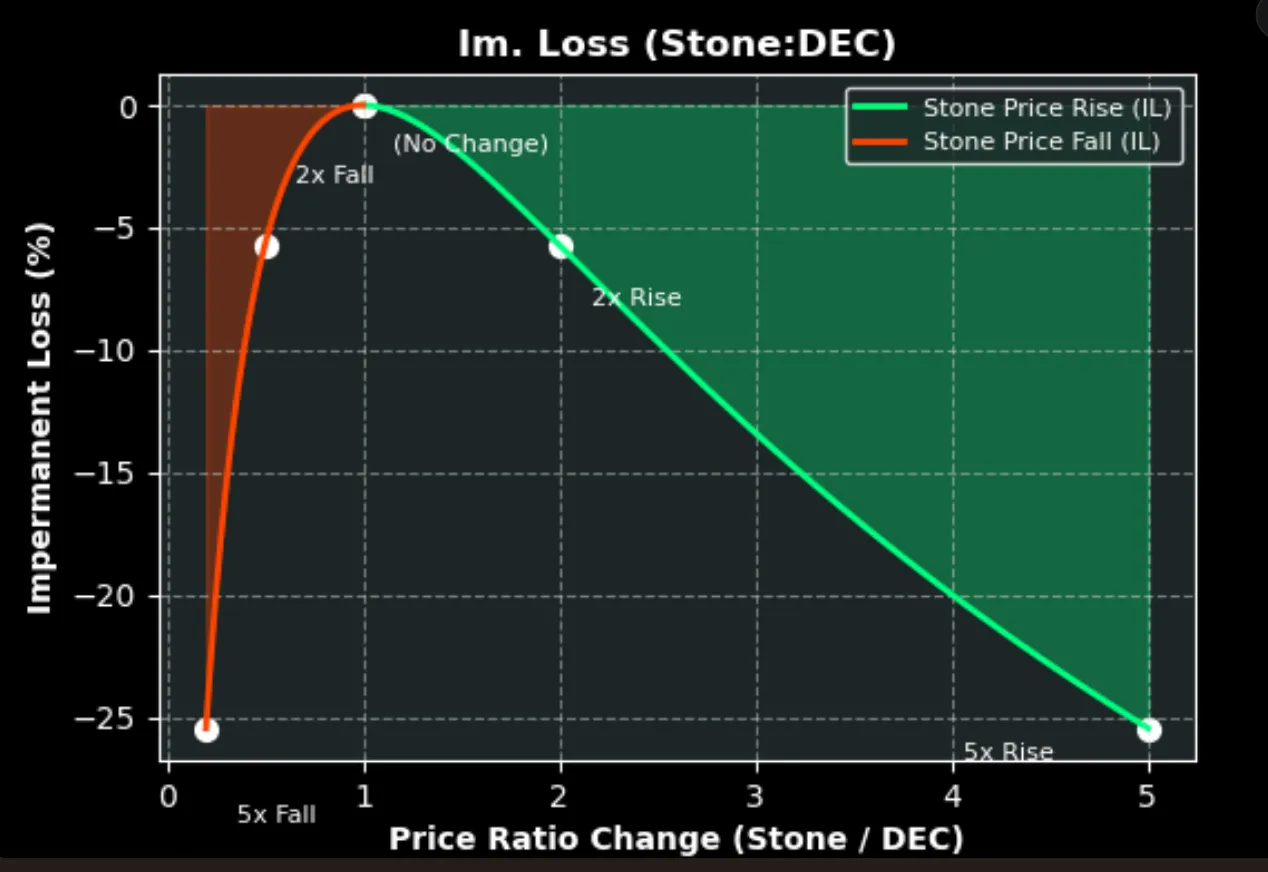
For example, in the Stone:DEC pool (1 Stone = 0.1 DEC initially, DEC stable at 1,000 DEC = $1). If someone deposits 100,000 Stone and 10,000 DEC (total $10), he/she holds $10 worth of stone and $10 worth of DEC, a total of $20 worth of total assets.

Now let us assume a 2x price rise of Stone to 0.2 DEC results in a pool value of ~$28.28 (70,710 Stone and 14,142 DEC), while holding just Stone yields $30 ($10 worth of stone now worth $20, plus $10 worth of DEC), incurring a ~5.7% IL.

The loss is "impermanent" because it’s only realized upon withdrawal and can diminish if prices revert to the initial ratio. The plot illustrates IL for 2x and 5x price changes, showing losses of ~5.7% and ~25.5%, respectively, highlighting the risk in volatile markets.

Important thing to note: IL is higher as the price departs more from the initial price.

But! We get the fees!

Right! You do. If you own 1% of the AMM pool for example, and if the pool pays 5% of the trading fees to the shareholders, that accumulates quickly. Yes? Think again. You must warm up to a concept of asymmetric risk.

Asymmetric Risk in the context of impermanent loss (IL) in the Stone:DEC liquidity pool refers to the uneven risk-reward profile faced by liquidity providers (LPs) compared to simply holding tokens.

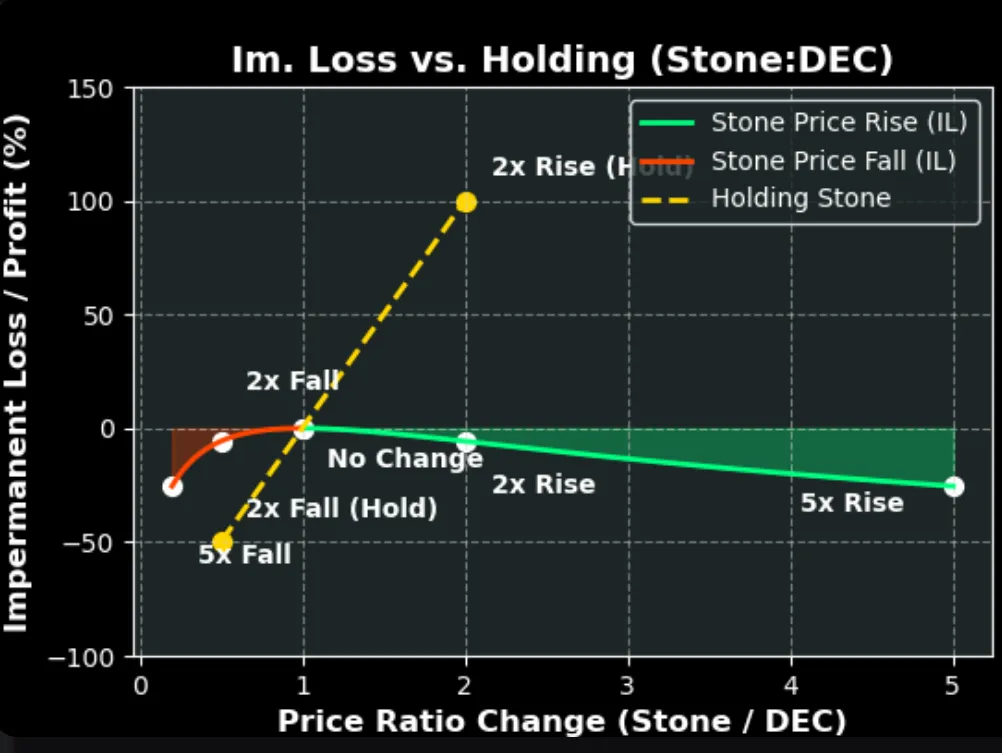
The 5% LP fee (from the 10% swap fee) can offset IL, but as calculated, offsetting a 5.7% IL for a 2x rally requires $11,400 in swap volume for a $200 stake (1% of a $20,000 pool). With a monthly trading volume of $14,000, fees are only ~$7 for a 1% LP (0.01 × 0.05 × $14,000), far short of the $57 needed, making IL a persistent risk.

In other words, if you hold $100 worth of stone (other is $100 worth of DEC which doesn't move lets say), and stone rally 2X, you now have $200 worth of stone plus $100 of DEC, a total of $300. But the same Stone and DEC left in the pool for 1 month after a 2X rally, now the total pool is worth $28,284. The 1% share of that is $282.84. Plus there is the $7 worth of fee, making the total to $282.84 + 7 = $289.84

Folks, that is less then $300, if you have done nothing and hold. I have highlighted the simplest scenario and perhaps the best case scenario. Everything else and higher volatility will make it worse.

PS. I don't want to sound Mr. Obvious, but if I am speculating rapid rally in the price of stone (or anything for the matter), why I would hold $100 worth of stone and $100 worth of DEC? I would just swap the DEC to stone and hold $200 worth of stone. Now with the 2X move, I might have $400 worth of stone, as opposed to $289.84 in the pool!

OUCH!

I want to add these two updated plots for the record, as they capture the exact numbers of Stone:DEC pool as of today

Constant Product Curve	Impermanent Loss (IL) Curve
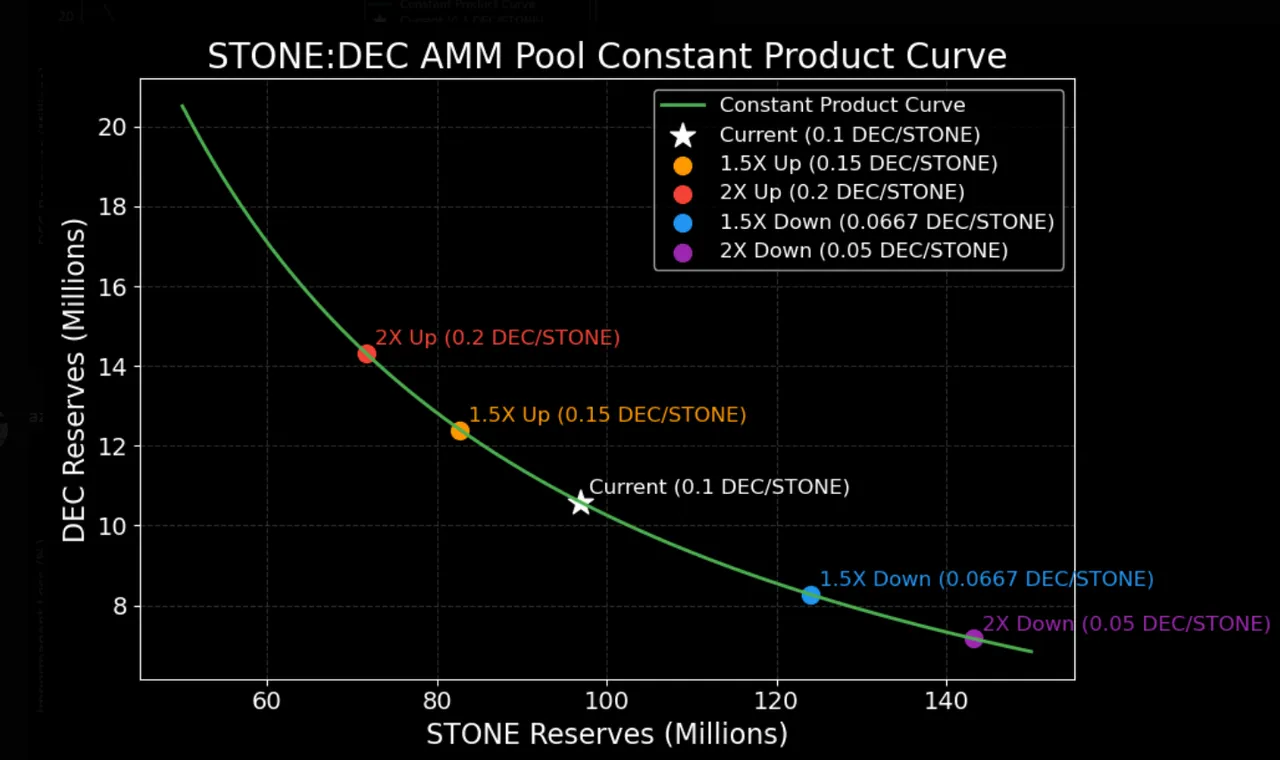