
When I solved this exercise in Code Wars there were no problems, however, none of the following 2 solutions are correct. Luckily I noticed this and realized that none of these methods were the ones I had used to solve the excercise, before posting it here like a crazy. So why am I bringing them anyway, you'll wonder? Because I am going to use them like an excuse to explain why such solutions are wrong and what is going on behind the scenes. Besides, thanks to this little mistake I found another solution that is more efficient.
But, what's the matter with these 2 methods? Easy! If, by a chance, one of them match the following test, they will fail in their job: passing the array ["North", "East", "West", "South"] as a parameter would return ["North", "South"] as a result, and this is completely wrong if we follow the rules of this exercise: it should've been [].
Cuando resolví este ejercicio en Code Wars no hubo ningún tipo de problemas, sin embargo, ninguna de las siguientes 2 soluciones son correctas. Por suerte rectifiqué a tiempo y me di cuenta de que ninguno de estos métodos eran los que había utilizado para resolverlo, antes de postearlo por aquí a lo loco ¿Entonces para qué los traigo, te dirás? Porque me sirven como excusa para explicar por qué dichas soluciones son erróneas y que está pasando por detrás. Además, gracias a esta pequeña equivocación me di cuenta de otra posible solución mucho más eficiente que la que había encontrado en primer lugar.
Pero, ¿qué ocurre con estos 2 métodos? Lo que pasa es que si, por casualidad, alguno de los 2 se encuentra con el siguiente test, fallará en hacer su tarea: al pasarle como parámetro el siguiente array["NORTH", "EAST", "WEST", "SOUTH"], nos devolverían como resultado["NORTH", "SOUTH"], lo cuál es incorrecto según las reglas de este ejercicio: debería ser[].
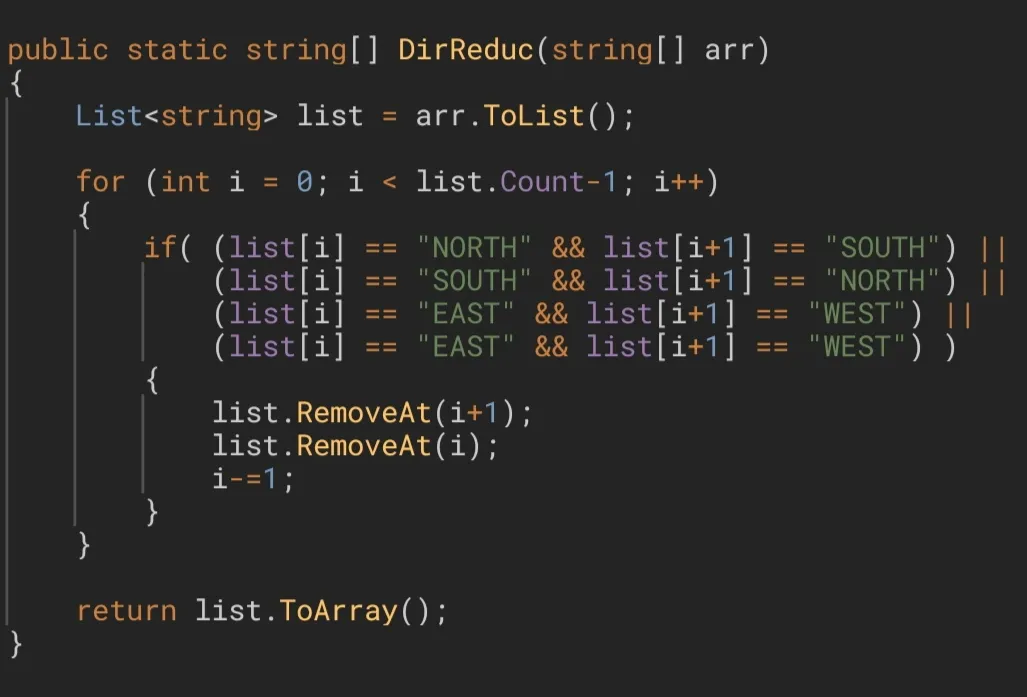
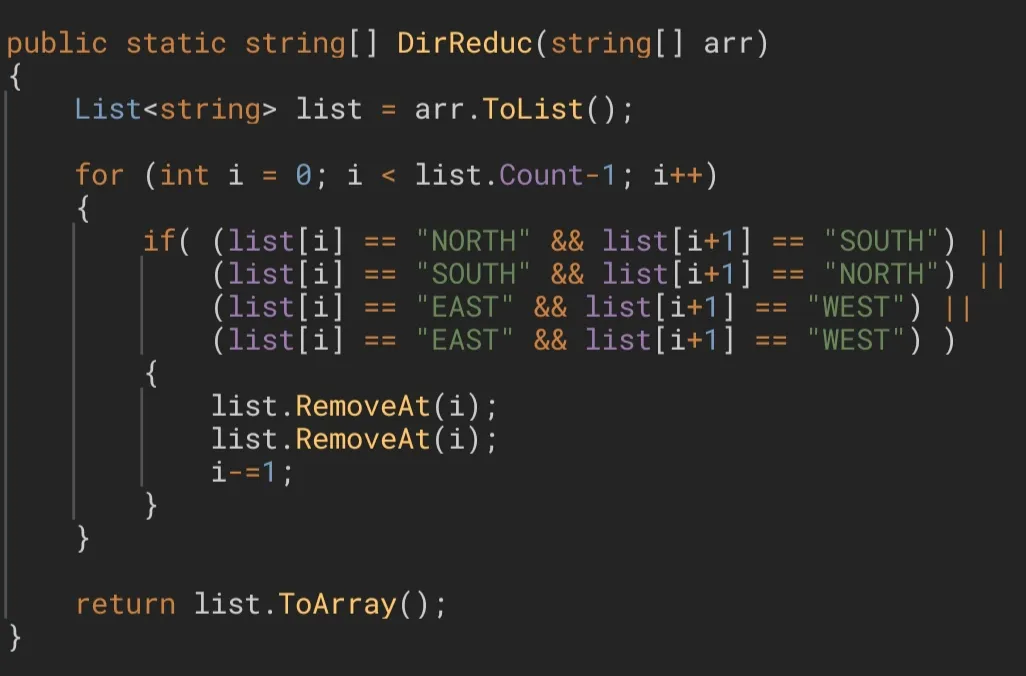
However, if we fix a little error in the code, we will solve this issue immediately:
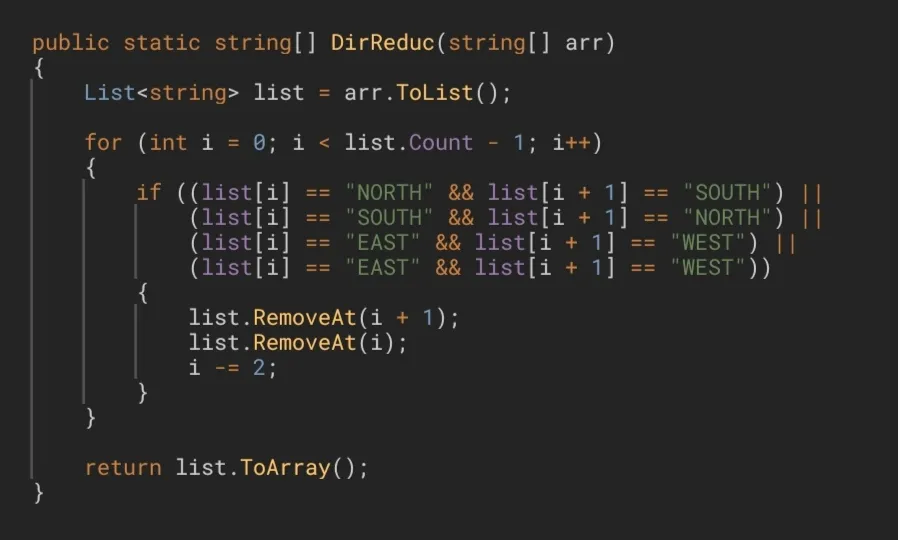
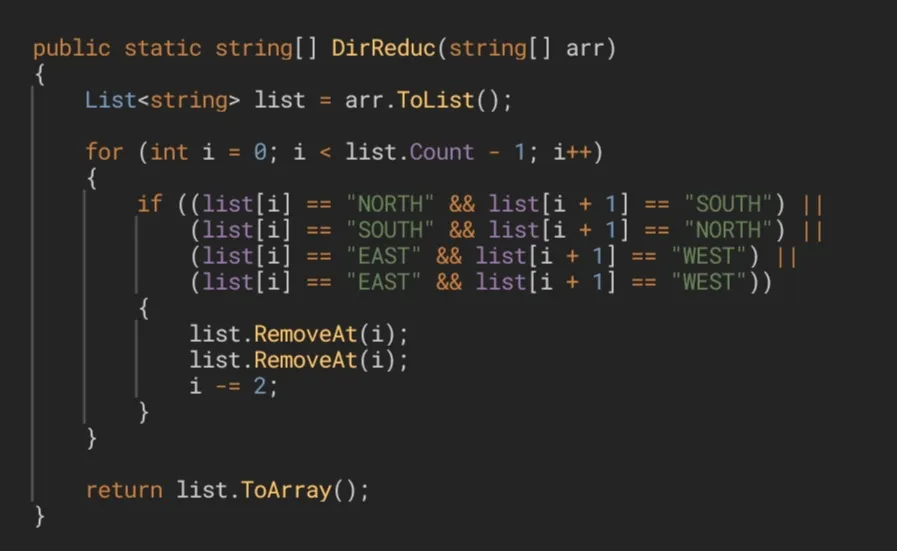
Sin embargo, si corregimos un pequeño error en el código, lo solucionaremos de inmediato.
The error can be small, but its implications are big. We better see what it is all about.
The statement of this excercise gives us vital information about it: "We can only reduce opposite directions that are directly next to each other". We know that removing elements from the center of a list makes those who were after the removed elements move to the left when rearranging the list. This leads us to conclude that in order to reduce the path of the man, we must not iterate over the list once, since 2 opposite directions that are far from each other can get close once adjacent pairs are eliminated. Of course, the creator of the kata provides us with this information in one of the examples.
El error puede ser pequeño, pero sus implicaciones son grandes. Mejor veamos de que se trata.
El enunciado del ejercicio nos da información vital al respecto: "Sólo podemos reducir los opuestos que están directamente uno al lado del otro". Sabemos que eliminar elementos del centro de una lista hace que aquellos que se encontraban después de los elementos removidos se muevan hacia la izquierda a la hora de rehacer la lista. Esto nos lleva a concluir que para reducir adecuadamente el camino del buen hombre, no debemos recorrer la lista una única vez, ya que 2 elementos que sean opuestos y se encuentren alejados uno del otro pueden acercarse una vez eliminados los pares adyacentes. Por supuesto, el creador del kata nos provee con esta información en uno de sus ejemplos.
The idea behind this solution was that, once we reduce 2 adjacent directions, we would make the value of the iterator equal to the index previous to where we were at (that is, i - 1). What I didn't notice was that this code would not take me to the previous element, but to the same one, since I forgot the i++ statement of the for loop. Therefore, for multiple chain reductions the algorithm would fail.
La idea detrás esta solución yace en que, una vez reducidas 2 direcciones adyacentes, haríamos que el valor de la variable iteradora fuera igual al índice anterior a dónde nos encontrábamos (o sea
i - 1). De lo que no me percaté fue que este código no me llevaba al elemento anterior, sino que me dejaba en el mismo elemento, ya que no tuve en cuenta eli++del buclefor. Por lo tanto, para múltiples reducciones en cadena el algoritmo fallaba estrepitosamente.
We can think that reducing the index by 2, instead of 1, would be enough, however, despite being necessary, this step is not enough. Reducing the index by 2 means restarting the searching from the preceding element, but the element whose index is equal to 0 (that is, the first one) is not preceded by any other. In other words, we would start searching from the outside of the array and would find ourselves dealing with an IndexOutOfRangeException. This is the only case that would give us problems, so the way of fixing it is very simple: if the reduction occurs when i = 0, we will detect this via an if statement and, only in that case, we will reduce its value by 1; in any other case we will reduce it by 2. This assures us that we will not look for any element with a negative index, while the for loop condition assures us that we will not look for any element with an index greater than or equal to the length of the array.
Podemos pensar que con reducir el índice en 2, en lugar de tan sólo en 1, bastaría, sin embargo, a pesar de ser necesario, no basta sólo con este paso. Reducir el índice en 2 significa recomenzar la búsqueda desde el elemento que le antecede, pero el elemento cuyo índice es igual a 0 (o sea el primero) no se encuentra precedido por ningún otro. En otras palabras empezaríamos a buscar desde fuera del array y nos encontraríamos con un
IndexOutOfRangeExceptionde manual. Este es el único caso que nos daría problemas, así que la manera de arreglarlo es bien sencilla: si la reducción ocurre siendoi = 0, detectaremos esto mediante un bloque de códigoify, sólo en ese caso, reduciremos su valor en 1; en cualquier otro caso la reducción se hará en 2. Esto nos asegura que no buscaremos ningún elemento con índice negativo, mientras que la condición del buclefornos asegura que no buscaremos ningún elemento con índice mayor o igual a la longitud del array.
Once all errors were corrected, the code for the solution would be like this:
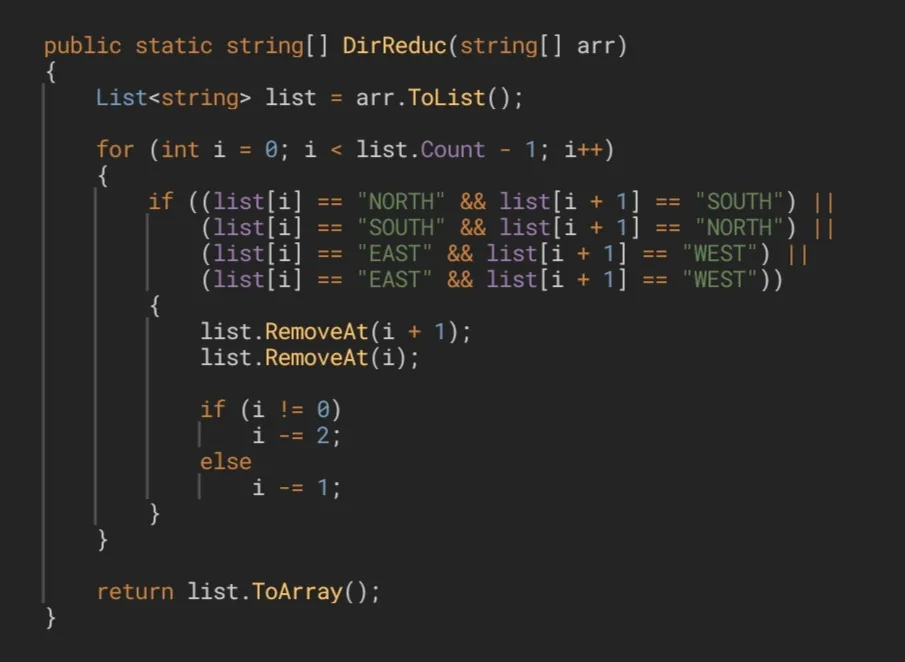
Una vez corregidos todos los errores, el código para la solución quedaría de esta manera.
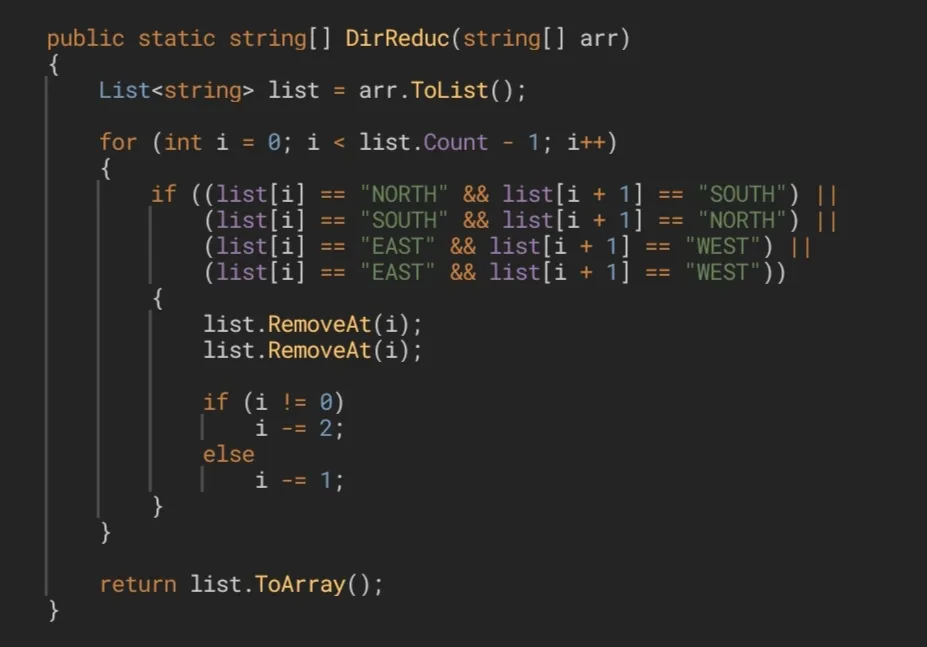
By the way, something that cannot be overlooked: let's analyze the lines of code that are responsible for removing the elements from the list. We have 2 different versions for the same operation. In the first version we remove the element that is located after the current one and, once this is done, we proceed to eliminate the current one. So far there is not any kind of problems, since the rearrangement of the elements of the list does not affect the element with index i (that is, the current one), because nothing makes it change its location or index. But if we do this the other way around (that is, removing i before i + 1), we will face with a problem, because if we remove the current element, all the elements following this one will move one step to the left, to rearrange the list, and that involves the element with index i + 1. For this reason, if we wanted to remove this element, actually we wouldn't be removing it, we would be removing the element that is after this one, and that is not what we are looking for to do. That is why in a second version we can see that, in this case, the next step is to remove the element with index i again, because when rearranging the list the adjacent element ended up taking its place.
A todo esto, una aclaración que no puede pasarse por alto: analicemos las líneas de código que se encargan de eliminar los elementos de la lista. Tenemos 2 versiones distintas para una misma operación. En una primera versión eliminamos el elemento posterior al actual y, una vez hecho esto, eliminamos el actual. Hasta aquí ningún tipo de problemas ya que, el reacomodamiento de los elementos de la lista, no afecta de ninguna manera al elemento con índice
i, pues nada lo hace cambiar de lugar. Pero si hacemos esto a la inversa (o sea, eliminariantes quei + 1) nos encontraremos con un problema, y es que si eliminamos el elemento actual, todos los elementos posteriores a él se desplazarán un lugar hacia la izquierda, para reacomodar y rehacer la lista, y eso involucra al elementoi + 1. Debido a esto, si quisiéramos eliminar este elemento, en realidad no lo estaríamos eliminando a él, sino al elemento posterior, y esto no es lo que estamos buscando. Es por eso que en una segunda versión podemos ver que, para este caso, la siguiente operación a realizar es eliminar de nuevo al elemento con índicei, porque, al rehacer la lista, el elemento adyacente acabó tomando su lugar.
Alternative solution [Solución alternativa]
Another posible solution could be the following, and this is the one that I had used in the first place:
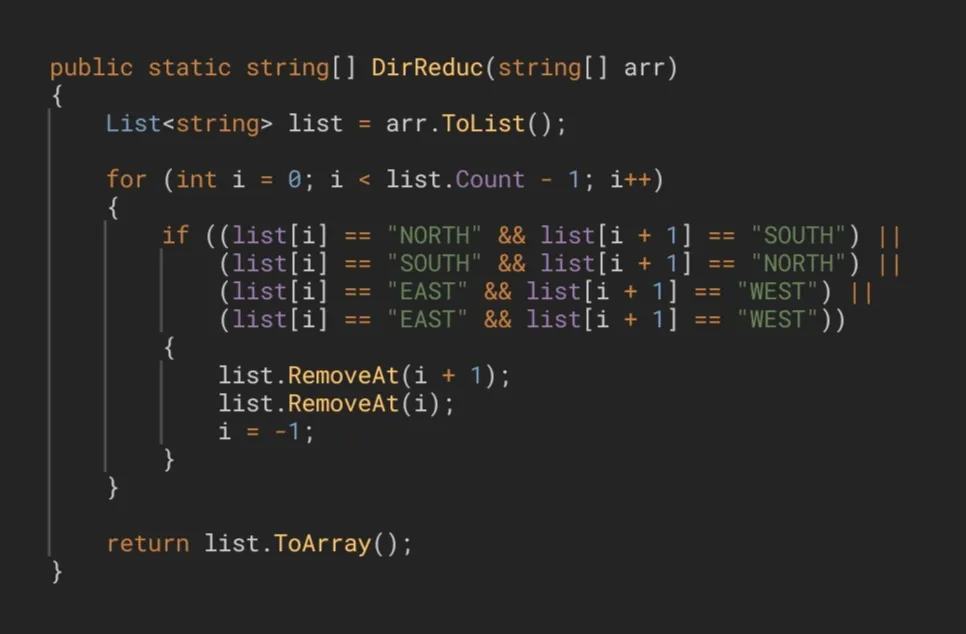
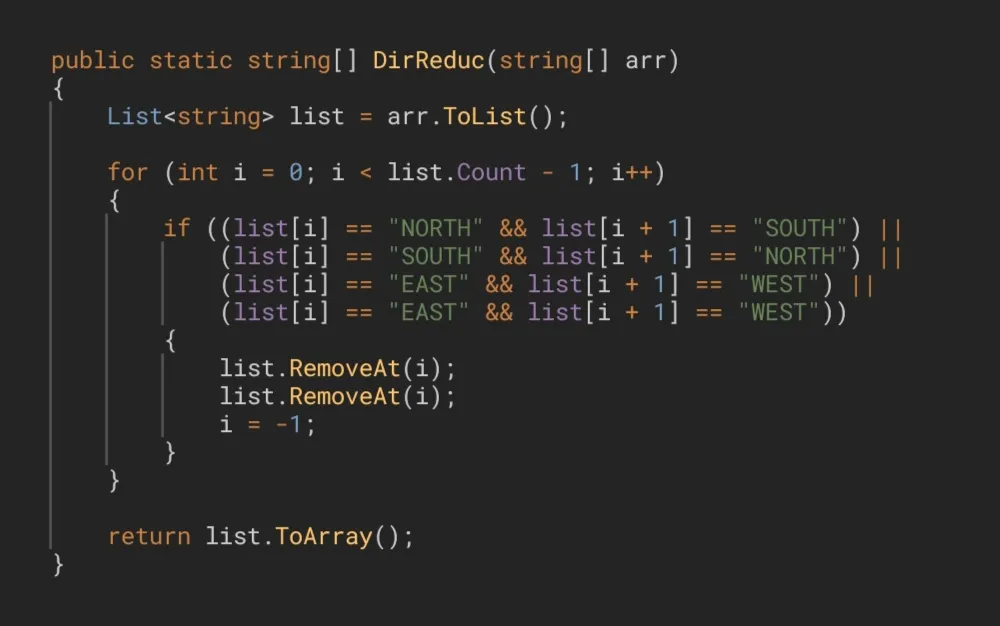
Otra posible solución podría ser esta, que es precisamente la que había utilizado en primer lugar.
This solution, although perfectly valid, are somewhat more inefficient than the previous one because, while that one restarted the searching from the previous element, this one starts from the first element of the array every time a reduction is made, which is completely unnecessary. When a directions reduction occurs, the elements that were on the right move to the left, to cover the hole that the adjacent elements had left. Therefore the only element that is involved in this operation, and the only one that has a possibility of meeting its pair, is the element prior to the removed elements. We don't need to start iterating over the loop from the beginning, since the first elements are not involved in any way; that is, nothing changes for any of them.
Esta solución, aunque perfectamente válida, es algo más ineficiente que la anterior ya que, mientras aquella volvía a comenzar la búsqueda a partir del elemento anterior, esta comienza desde el primer elemento del array cada vez que una reducción es realizada, lo cual es completamente innecesario. Cuando una reducción de direcciones ocurre, los elementos que se encontraban a la derecha son acercados, para cubrir el hueco que aquellos 2 habían dejado. Por tanto y demás el único elemento que se encuentra implicado en esta operación, y que tiene posibilidades de encontrarse con su par, es el elemento anterior a los elementos reducidos. No necesitamos comenzar a recorrer el bucle desde el principio, ya que los primeros elementos no se ven implicados de ninguna manera, es decir, nada cambia para ellos.
English translation made with DeeplTranslate
Traducción al inglés hecha con DeeplTranslate