Hey everyone,
After my last post about the mathematical fairness of the Ultimate Dice Roller, I got some excellent feedback. The gist of it was that a normal distribution over a large scale is a good start, but it doesn't tell the whole story about randomness. The feedback suggested looking into the entropy of the results to get a better measure of their unpredictability.
After a trip down a Wikipedia rabbit hole, I put together a new script to measure the Shannon entropy of the dice roll data. In simple terms, entropy is a measure of surprise or uncertainty. For a fair six-sided die, the ideal entropy is (log2(6)) about 2.585 bits. The closer our measured entropy is to that ideal value, the more unpredictable and fair the rolls are.
The Results
The script I wrote analyzes the dataset of 5,000 3d6 rolls from the last post. It calculates the Shannon entropy based on the frequency of each die face (1 through 6) and compares it to the ideal value. A total of 15,000 dice with 6 sides were compared.
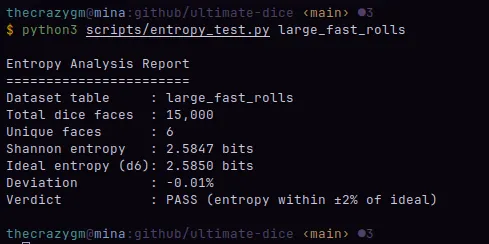
The analysis of the large_fast_rolls dataset shows a Shannon entropy of 2.5847 bits. This results in a deviation of just -0.01% from the ideal entropy for a fair six-sided die. The verdict from the script is a definite PASS, as the entropy is well within the ±2% tolerance for an ideal distribution.
I also created a script to visualize the entropy on a binary entropy curve. This plot shows how the probability of each individual face contributes to the overall entropy of the system.
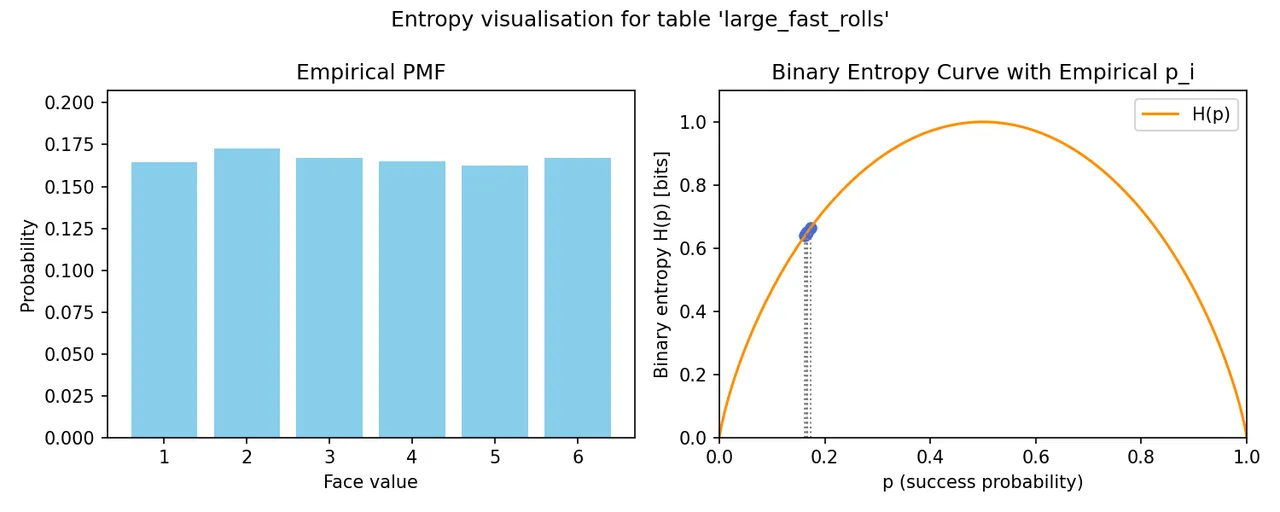
While the complex math behind the NIST publications suggested in the comments is a bit beyond me, this analysis gives me a high degree of confidence. So, I am once again going to say that yes, the Ultimate Dice Roller is mathematically fair.
The scripts are also in the repository here.
As always,
Michael Garcia a.k.a. TheCrazyGM