Hey everyone,
The other day, @ecoinstant posed an excellent question about the Ultimate Dice Roller: we know it's provably fair, but is it mathematically fair? In other words, over a large number of rolls, does it produce a statistically even distribution?
I thought that was a great question to dig into. To test it, I added some scripts to the project's GitHub repository to simulate rolling 3d6 thousands of time. A 3d6 roll is common for generating character stats in old-school D&D, and it should produce a nice bell curve distribution of results from 3 to 18.
Test 1: 100 Rolls, As Fast as Possible
First, I had the script roll 100 times as quickly as possible. Because the rolls happen so fast, they all use the same seed data from the same Hive block. The result was, as expected, not very random at all.
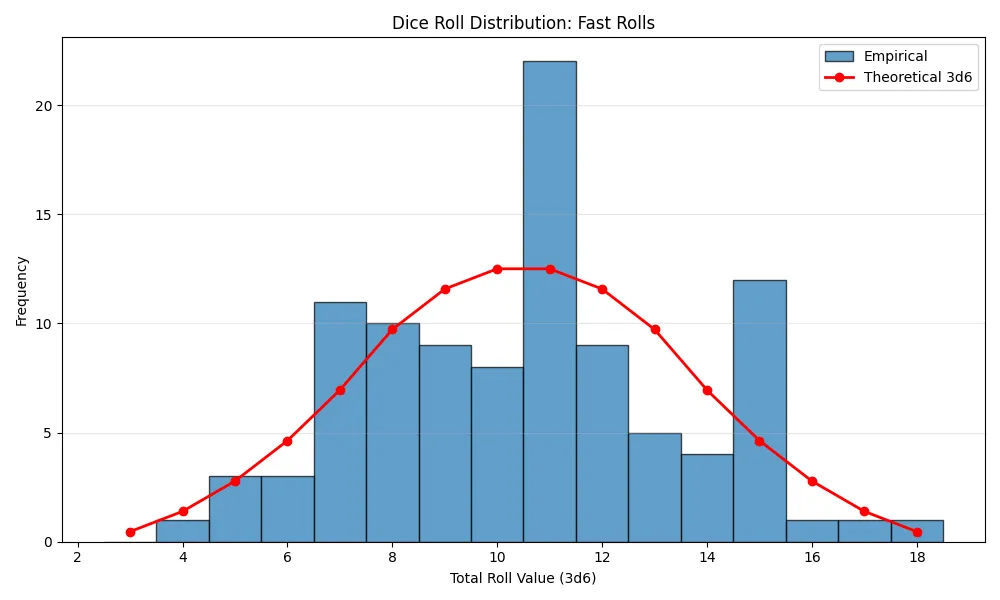
Test 2: 100 Rolls, With a Delay
Next, I had the script wait a few seconds between each of the 100 rolls. This pause allows the blockchain to produce new blocks, ensuring that each roll gets a new, unique seed (server seed, client seed, and nonce). The result was a much better, more varied distribution.
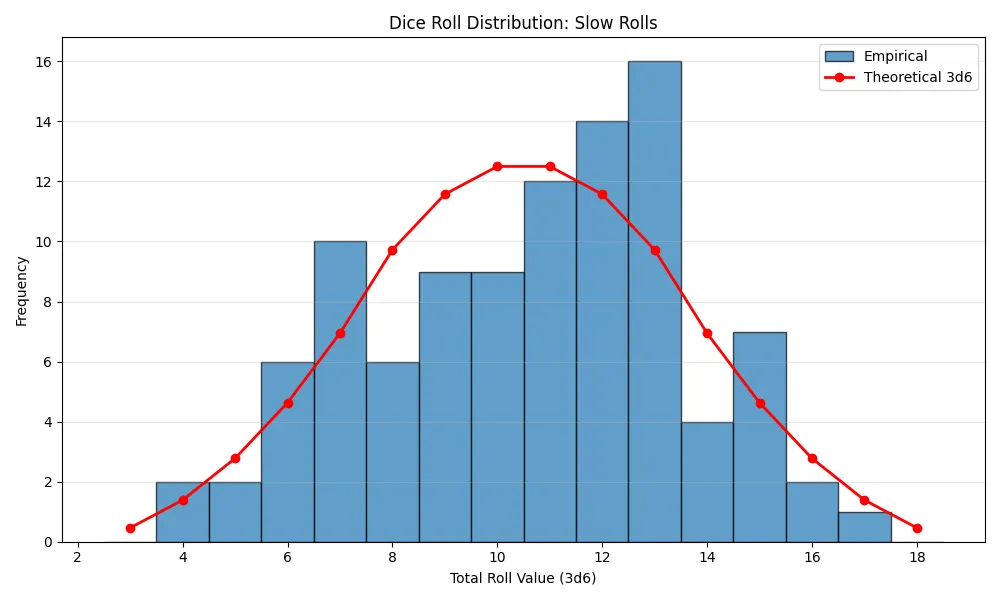
Test 3: 5,000 Rolls
Finally, for the ultimate test, I had the script roll the dice 5,000 times. I did this as fast as possible because waiting a few seconds for each roll would have taken over four hours (5,000 rolls x 3 seconds/roll ≈ 4.16 hours). The script rapidly requested rolls, and the server's "salting" mechanism ensured each roll was still unique even if the block data was the same.
The final chart speaks for itself.
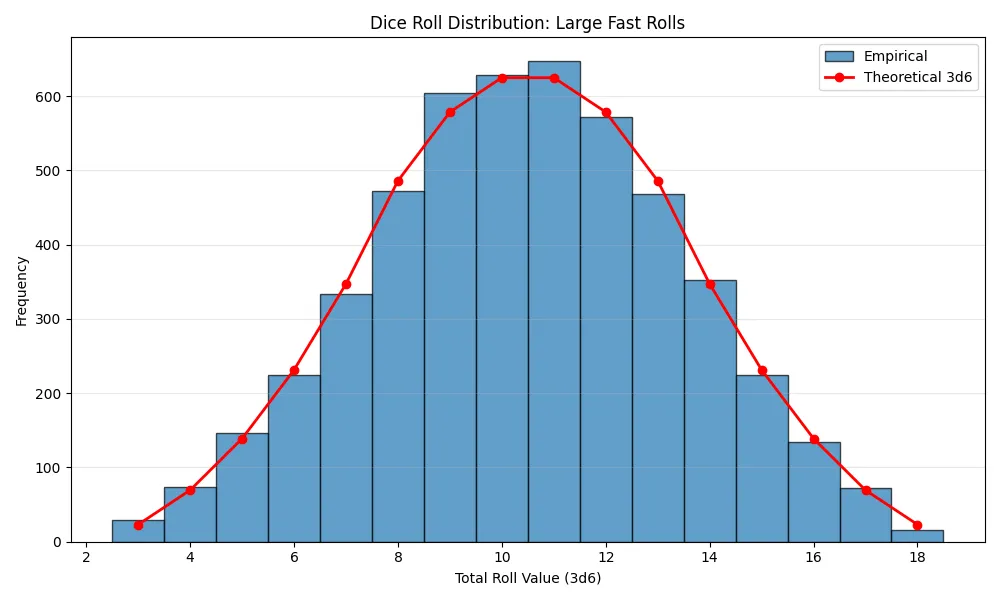
With a large enough sample size, the dice roller produces a beautiful, statistically fair bell curve, right on the money. So, the answer is yes, the Ultimate Dice Roller is not only provably fair but mathematically fair as well.
If this kind of statistical analysis interests you, feel free to take a look at the scripts directory in the GitHub repo to see how the tests were run and the plots were generated.
As always,
Michael Garcia a.k.a. TheCrazyGM