Saludos amigos de la comunidad hive.
En esta oportunidad alternando contenido, un poco de ingeniería de petróleo y en otras ocasiones como es el caso de este post con algo de cálculo infinitesimal, quizás para muchos no es un secreto que me fascina el cálculo y aprovechó la oportunidad de este espacio que me da la comunidad de #stemsocial y #cervantes para mantenerme actualizado con este conocimiento, ya que para mí es útil mantenerme actualizado porque actualmente me encuentro dictado clases de cálculo a distancia en la Universidad Experimental Sur del Lago Jesús María Semprum (UNESUR).
Introducción
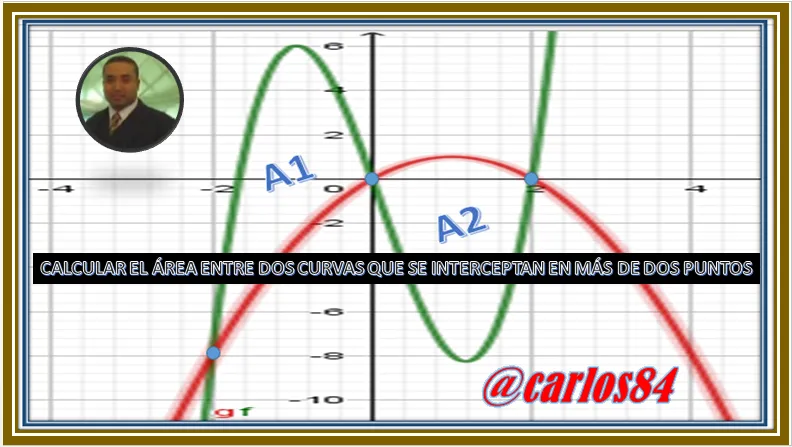
Existen funciones polinómicas que cuando se grafican el plano cartesiano se cortan en más de dos puntos, haciendo que se generen varias regiones del plano que se vuelven muy interesantes para el cálculo de área. Para calcular el área total de las subregiones que surgen de las sub áreas generadas por la intersección de las dos funciones, simplemente se tiene que calcular el área total sumando todas las áreas de las distintas regiones que salgan de la intercepción de las dos curvas.
Recursos empleados para la explicación
La idea es explicar un ejemplo en donde se pueda mostrar las funciones que se interceptan en más de dos puntos y a la vez se calcule el área total.
Para ello voy a realizar un gráfico empleando el software geogebra 5.0 y a editarlo en Microsoft PowerPoint.
Una vez obtenido el gráfico voy a emplear una de las aplicaciones que tiene la integral para calcular el área entre curvas, teniendo en cuenta el teorema fundamental del cálculo para resolver integrales definidas.
Al mismo tiempo todas las ecuaciones que se deduzcan para dicha explicación las voy a generar empleando las herramientas de inserción de ecuaciones que tiene el programa Microsoft Word.
Ejemplo de un ejercicio para encontrar el área total entre una función cúbica y una función cuadrática que se cortan en más de dos puntos
Encontrar el área de la región comprendida entre las siguiente funciones:
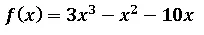
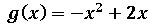
Para resolver este ejercicio lo primordial es saber la región del plano que delimita los puntos de intersección entre estas dos curvas, para ello voy a emplear el software geogebra 5.0 y editar en Power point para mostrarles dicha región del plano cartesiano:
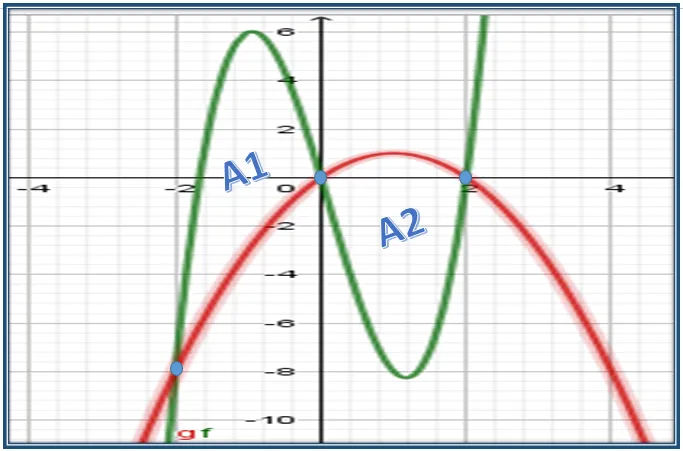
Como se puede observar en la imagen anterior para calcular el área total se tienen que sumar A1 + A2, es decir At= A1+A2.
Para calcular el área 1 tomamos en cuenta la integral que va de -2 a 0 de la curva que está por encima (función cúbica) menos la curva que está por debajo (función cuadrática), por lo tanto el cálculo del área 1 queda de la siguiente forma:
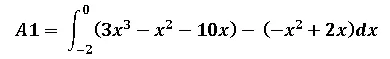
El procedimiento es resolver esa integral definida aplicando el teorema fundamental del cálculo:
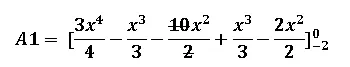
Luego realizamos la cancelación de términos iguales con diferente signo:
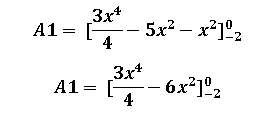
Si realizamos la sustitución del límite superior en la variable x nos va a dar cero, por lo tanto realizamos la sustitución del límite inferior, solo que debemos tomar en cuenta que lleva el signo negativo por delante:
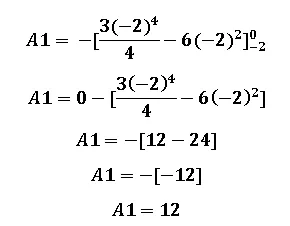
Una vez calculado el área 1 procedemos a calcular el área 2 de forma similar en cómo calculamos el área 1:
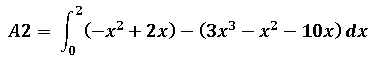
Se simplifica los términos antes de integrar quedando de la siguiente manera:
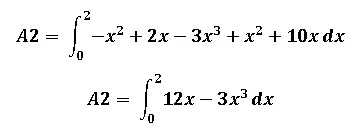
Resolvemos la integral:
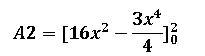
Aplicamos el teorema fundamental del cálculo:
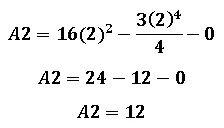
Por lo tanto el cálculo del área total de intersección es At= A1+A2, lo cual implica que At= 12 + 12 = 24 Unidades de área.
Conclusión de aprendizaje
Es importante que este tipo de regiones del plano en el que dos funciones reales se corten en más de dos puntos se pueden seccionar en diferentes partes y que se tome en cuenta para el cálculo de cada sección las aplicaciones de la integral entre las que se encuentran colocar la curva que esté por encima menos la que se encuentre por debajo y como límites de integración se toma en cuenta como límite inferior el que está primero de izquierda a derecha y como límite superior el número que le sigue al límite inferior.
Referencias recomendadas para ampliar el conocimiento del cálculo
Cálculo completo Vol 1 y 2 9na Edición Ron Larson & Bruce H. Edwards
Observaciones
Todas las imágenes son de mi autoría y fueron elaboradas empleando las herramientas de diseño de Microsoft PowerPoint y el software geogebra 5.0