Entre los distintos tipos de Ecuaciones Diferenciales, tenemos aquellas que pueden reducirse a la forma homogénea y juegan un papel clave por su estructura y métodos de resolución. Estas Ecuaciones Diferenciales tienen la Forma:
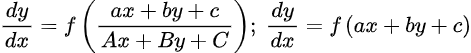
Las Ecuaciones Diferenciales Reducibles a Homogéneas permiten, mediante un cambio de variable adecuado, transformar una Ecuación no Homogénea en una Homogénea, facilitando así su análisis y solución. Dichas Ecuaciones Diferenciales están formadas por coeficientes lineales de la forma:
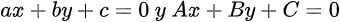
Con base a la posición relativa de las dos rectas en el plano, estudiaremos dos casos, cuando las rectas se cortan (tienen un punto en común) y cuando las rectas son paralelas.
En esta publicación se presentan 10 ejercicios resueltos de Ecuaciones Diferenciales que pueden ser Reducidas a Homogéneas. Cada ejercicio incluye una explicación paso a paso, desde la identificación del tipo de ecuación, el cambio de variable necesario, hasta la obtención de la solución general. El objetivo es proporcionar una guía clara y didáctica para estudiantes y docentes interesados en dominar este método y aplicarlo a problemas reales.
¿Listo para comenzar este viaje de aprendizaje? ¡Vamos a resolver juntos estas Ecuaciones y descubrir el poder de la transformación Homogénea!



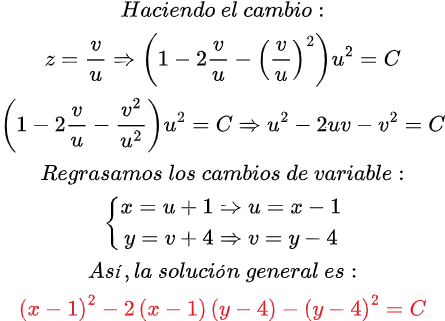
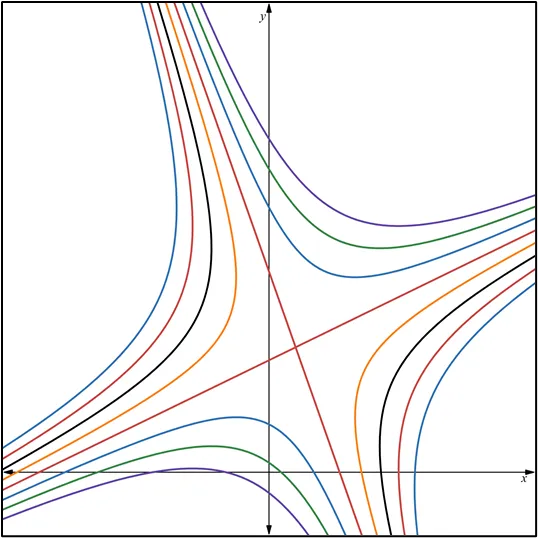





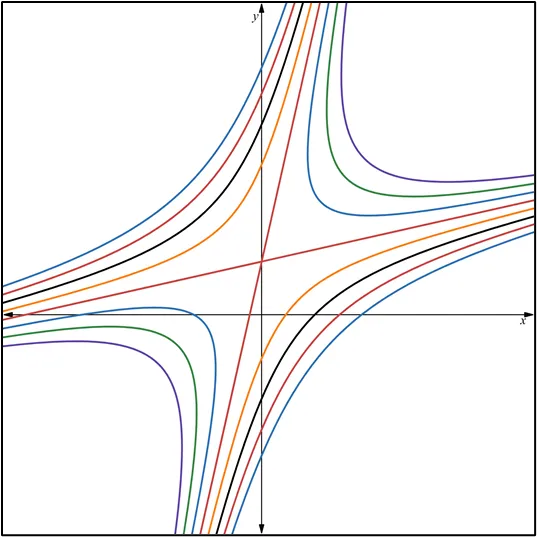
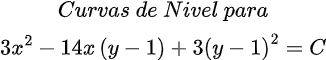


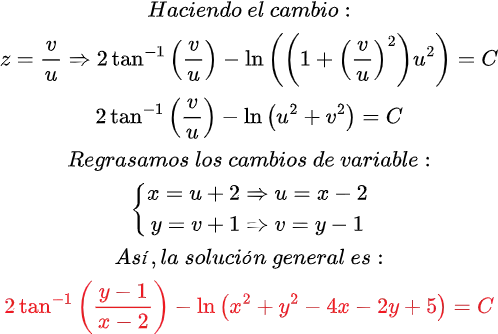
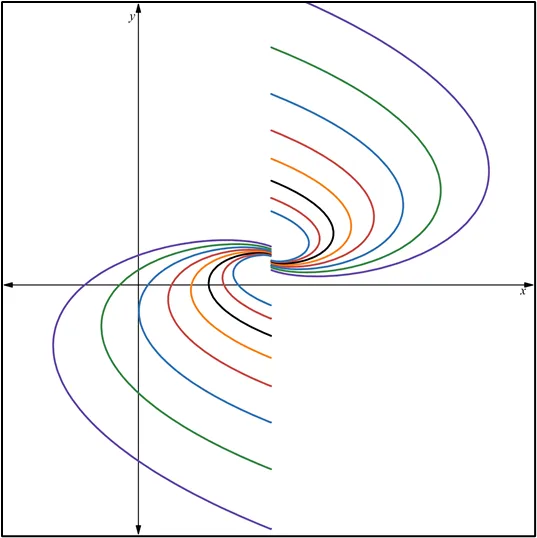
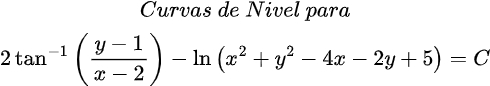


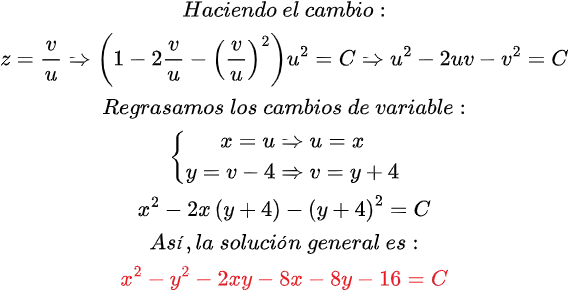
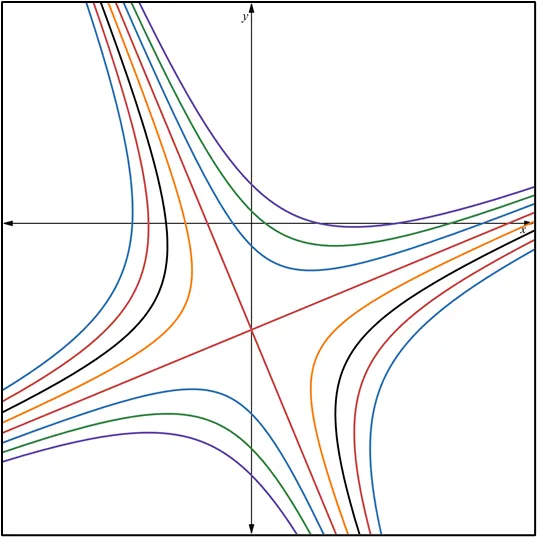


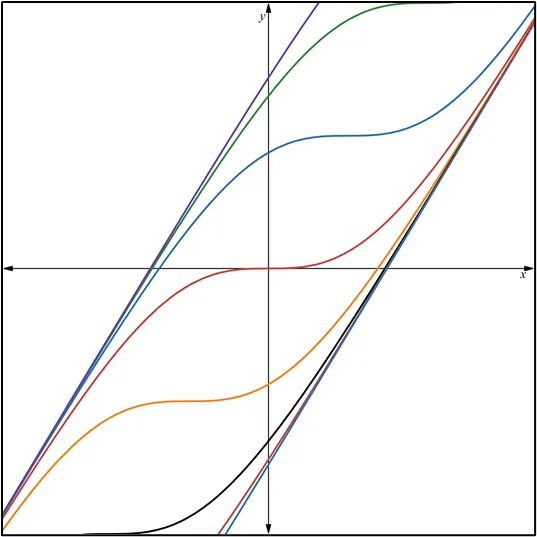
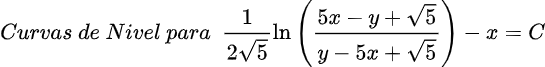

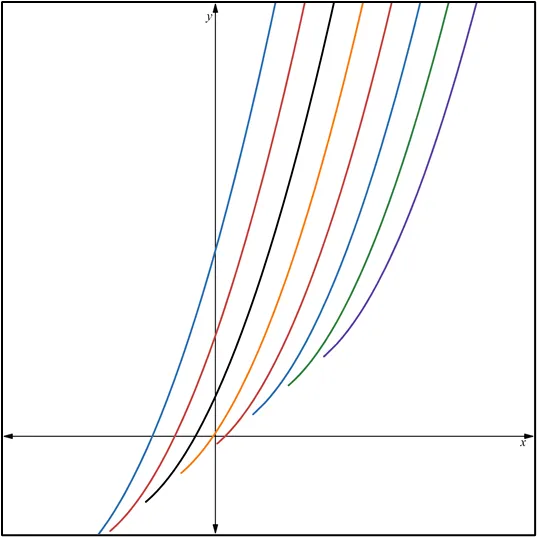
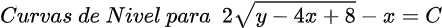

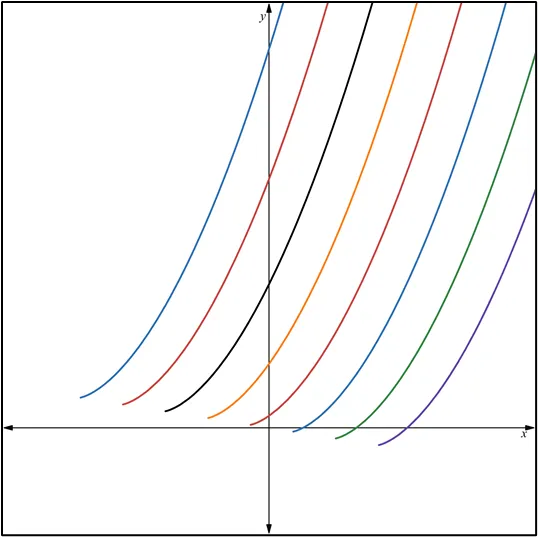



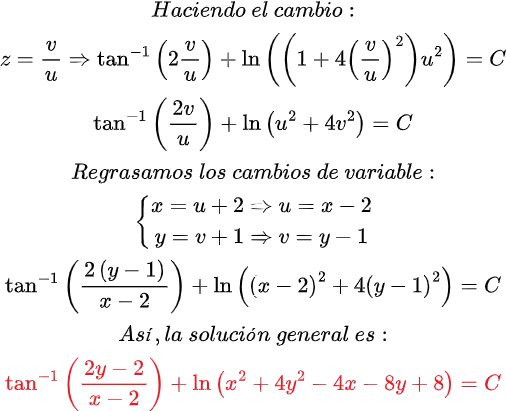
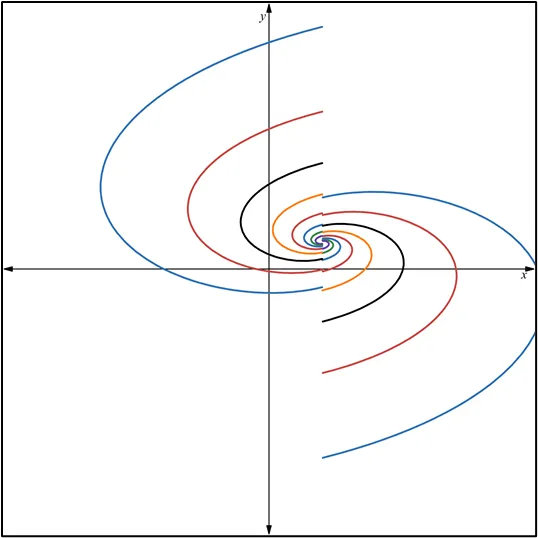




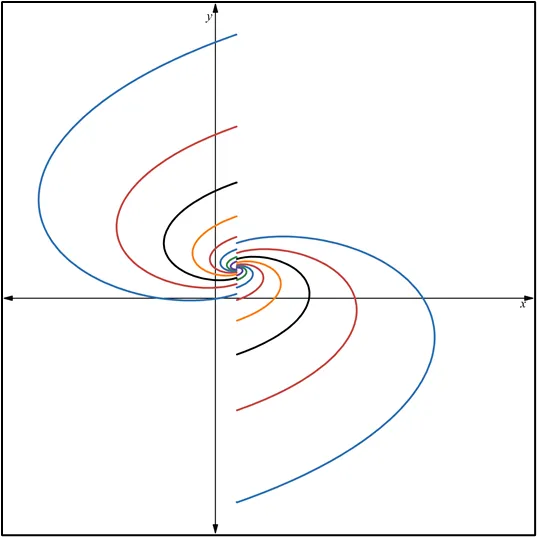
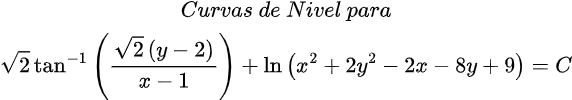

Quisiera expresar mi más sincero agradecimiento a todos los lectores de Hive Blog que han seguido mis publicaciones sobre Ecuaciones Diferenciales Reducibles a Homogéneas. Su interés y participación enriquecen este espacio y me motivan a continuar compartiendo conocimientos. Espero que el contenido siga siendo de utilidad y contribuya a su crecimiento académico. ¡Gracias por su confianza y apoyo constante!
DIOS LOS BENDIGA

1.- A. Kiseliov, M. Krasnov y G. Makarenko. Problemas de Ecuaciones Diferenciales Ordinarias. Editorial MIR, 1984.
2.- Acero, Ignacio. Ecuaciones Diferenciales Teoría y Problemas. Editorial Tébar, 2007.
3.- Boyce, William E., DiPrima, Richard C., Meade, Douglas B. Ecuaciones Diferenciales Elementales y Problemas de Valores en la Frontera. Editorial Wiley, 2012.
4.- C. Henry Edwards, David E. Penny. Ecuaciones Diferenciales. Editorial Pearson Educación de México, 2001.
5.- Earl D. Rainville, Phillip E. Bedient, Richard E. Bedient. Ecuaciones Diferenciales. Editorial Pearson Educación, 1997.
6.- G. Baranenkov, B. Demidovich, V. Efimenko, S. Kogany, G. Lunts, E. Porshneva, E. Sichova, S. Frolov, R. Shostak y A. Yanpolskí. Problemas y Ejercicios de Análisis Matemático. Editorial MIR, 1967.
7.- Jiménez López, Víctor. Ecuaciones Diferenciales: cómo aprenderlas, cómo enseñarlas. EDITUM, 2000.
8.- Larson, Robert P. Hostetler, Roland E. Cálculo y Geometría Analítica. Volumen 2. McGraw Hill, 1995.
9.- Morris Tenenbaum, Harry Pollard. Ecuaciones Diferenciales Ordinarias. Editorial Dover, 1963.
10.- Quintana, Pedro, Villalobos Eloísa, Cornejo María. Métodos de Solución de Ecuaciones Diferenciales y Aplicaciones. Editorial Reverte, 2008.
11.- R. Kent Nagle, Edward B. Saff, Arthur David Snider. Ecuaciones Diferenciales y Problemas con Valores en la Frontera. Editorial Pearson Educación de México, 2005.
12.- Shepley L. Ross. Ecuaciones Diferenciales. Editorial Reverté, 1992.
13.- Zill, Dennis G. Ecuaciones Diferenciales con Aplicaciones. Grupo Editorial Iberoamérica, 1988.
la página web: https://www.desmos.com/calculator/frx7bimvdd?lang=es.