Las Ecuaciones Diferenciales son una de las herramientas más poderosas para describir procesos en física, biología, economía y muchas otras áreas. Sin embargo, enfrentarse a ellas puede parecer un reto abrumador, especialmente cuando se trata de ecuaciones que, a simple vista, no son homogéneas, pero que pueden transformarse y resolverse con ingenio.
En esta publicación, te invito a sumergirte en el fascinante mundo de las Ecuaciones Diferenciales Reducibles a Homogéneas. A través de la solución detallada de 10 ejercicios cuidadosamente seleccionados, descubrirás:
1.- Cómo identificar ecuaciones que pueden transformarse en homogéneas.
2.- Estrategias paso a paso para aplicar cambios de variable y simplificar el problema.
3.- La satisfacción de ver cómo un problema complejo se convierte en una solución elegante y comprensible.
Resolver estos ejercicios no solo fortalecerá tu dominio técnico, sino que también te permitirá apreciar la belleza y utilidad de las matemáticas como lenguaje universal para resolver problemas reales. Además, al seguir cada solución detallada, podrás desarrollar tu propio razonamiento conceptual y ganar confianza para enfrentar nuevos desafíos matemáticos.
¡Atrévete a descubrir el potencial de las Ecuaciones Diferenciales y lleva tus habilidades matemáticas al siguiente nivel!








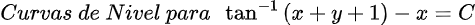

















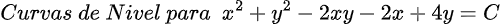


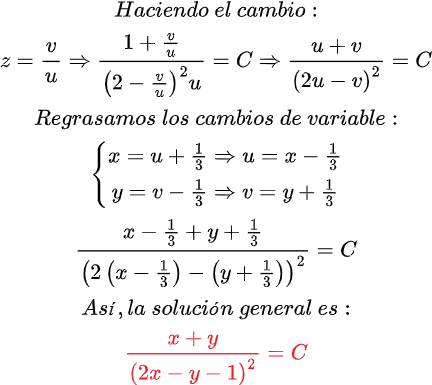





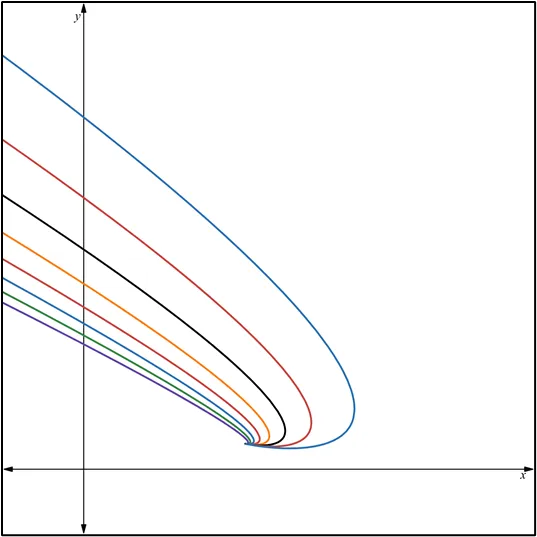


Quisiera expresar mi más sincero agradecimiento a todos los lectores de Hive Blog que han seguido mis publicaciones sobre Ecuaciones Diferenciales. Su interés y participación enriquecen este espacio y me motivan a continuar compartiendo conocimientos. Espero que el contenido siga siendo de utilidad y contribuya a su crecimiento académico. ¡Gracias por su confianza y apoyo constante!
DIOS LOS BENDIGA

1.- A. Kiseliov, M. Krasnov y G. Makarenko. Problemas de Ecuaciones Diferenciales Ordinarias. Editorial MIR, 1984.
2.- Acero, Ignacio. Ecuaciones Diferenciales Teoría y Problemas. Editorial Tébar, 2007.
3.- Boyce, William E., DiPrima, Richard C., Meade, Douglas B. Ecuaciones Diferenciales Elementales y Problemas de Valores en la Frontera. Editorial Wiley, 2012.
4.- C. Henry Edwards, David E. Penny. Ecuaciones Diferenciales. Editorial Pearson Educación de México, 2001.
5.- Earl D. Rainville, Phillip E. Bedient, Richard E. Bedient. Ecuaciones Diferenciales. Editorial Pearson Educación, 1997.
6.- G. Baranenkov, B. Demidovich, V. Efimenko, S. Kogany, G. Lunts, E. Porshneva, E. Sichova, S. Frolov, R. Shostak y A. Yanpolskí. Problemas y Ejercicios de Análisis Matemático. Editorial MIR, 1967.
7.- Jiménez López, Víctor. Ecuaciones Diferenciales: cómo aprenderlas, cómo enseñarlas. EDITUM, 2000.
8.- Larson, Robert P. Hostetler, Roland E. Cálculo y Geometría Analítica. Volumen 2. McGraw Hill, 1995.
9.- Morris Tenenbaum, Harry Pollard. Ecuaciones Diferenciales Ordinarias. Editorial Dover, 1963.
10.- Quintana, Pedro, Villalobos Eloísa, Cornejo María. Métodos de Solución de Ecuaciones Diferenciales y Aplicaciones. Editorial Reverte, 2008.
11.- R. Kent Nagle, Edward B. Saff, Arthur David Snider. Ecuaciones Diferenciales y Problemas con Valores en la Frontera. Editorial Pearson Educación de México, 2005.
12.- Shepley L. Ross. Ecuaciones Diferenciales. Editorial Reverté, 1992.
13.- Zill, Dennis G. Ecuaciones Diferenciales con Aplicaciones. Grupo Editorial Iberoamérica, 1988.
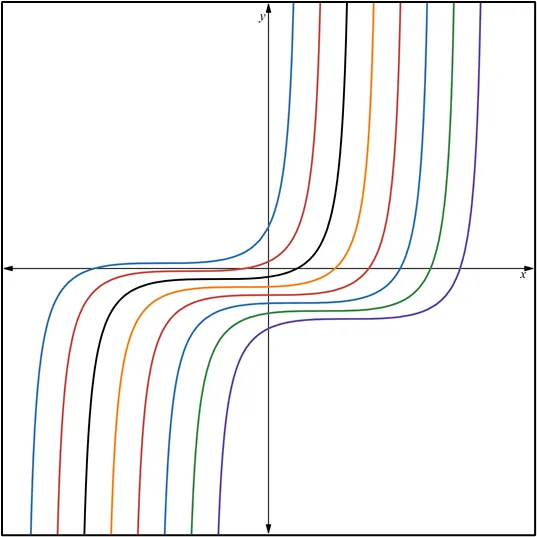
la página web: https://www.desmos.com/calculator/frx7bimvdd?lang=es.