¡Hola querida comunidad científica de #Hive, reciban todos un cordial saludo!🖐
Hello dear #Hive scientific community, receive warm greetings from all of you!🖐
Hace una semana estuvimos dando la introducción a las operaciones con vectores tanto numérica y gráfica. En ésta ocasión abordaremos el tema de la diferencia de vectores, conjuntamente con algunas operaciones de vectores.
A week ago we were giving an introduction to vector operations both numerically and graphically. This time we will deal with the topic of vector difference, along with some vector operations.

Imagen realizada con la página web de diseño gráfico y composición de imágenes Canva // Image made with the graphic design and image composition website Canva.
Antes de hablar de la diferencia de vectores, es propicio conocer sobre los vectores opuestos. Resulta que cuando se realiza la suma de Vectores y esta da como resultado ser nula, se dice que los vectores son opuestos. Su definición dice que “ Dos vectores son opuestos si tienen el mismo módulo y dirección pero tienen sentidos contrarios”.
Before talking about the difference of vectors, it is appropriate to know about the opposite vectors. It turns out that when the sum of vectors is performed and the result is zero, it is said that the vectors are opposite. Its definition says that "Two vectors are opposite if they have the same module and direction but have opposite directions".
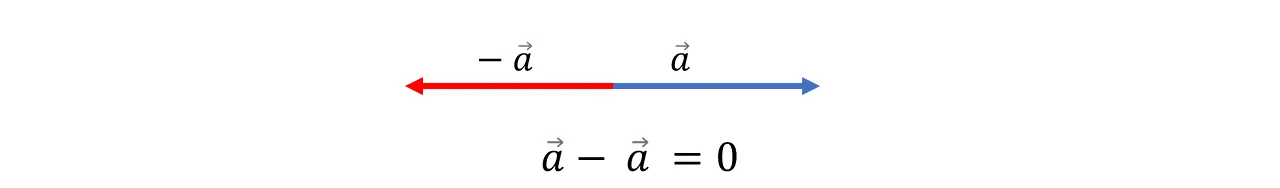
Diferencia de Vectores (Método gráfico) // Vector Difference (Graphical Method)
En la publicación anterior pudimos analizar la suma gráfica de vectores, ahora es propicio conocer cómo se restan los vectores de manera gráfica. Para restar los vectores A - B se suma el vector A y el opuesto del vector B.
In the previous publication we were able to analyze the graphical addition of vectors, now it is appropriate to know how to subtract vectors graphically. To subtract vectors A - B we add vector A and the opposite of vector B.
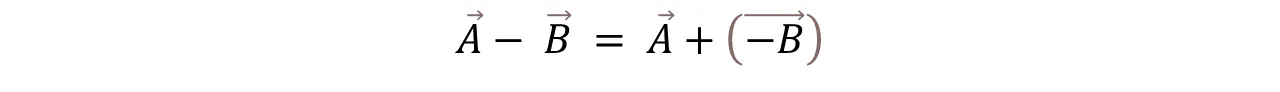
Veamos un ejemplo: Dados los vectores A y B efectuar A - B
Let's see an example: Given the vectors A and B effect A - B

Para poder calcular A - B primero hay que trazar el vector opuesto - B, el cual tiene el mismo módulo y dirección que B pero con sentido contrario.
A - B es el vector que sale del origen del vector A y llega al extremo del vector opuesto - B.
Analicemos un problema con coordenadas. Dados los vectores C = (-2,1) y D = (3,2), calcular numérica y gráficamente el vector C - D.
Primero graficamos los vectores C y D
In order to calculate A - B we must first draw the opposite vector - B, which has the same modulus and direction as B but with opposite direction.
A - B is the vector that leaves the origin of the vector A and arrives at the end of the opposite vector - B.
Let's analyze a problem with coordinates. Given the vectors C = (-2,1) and D = (3,2), calculate numerically and graphically the vector C - D.
First we graph the vectors C and D
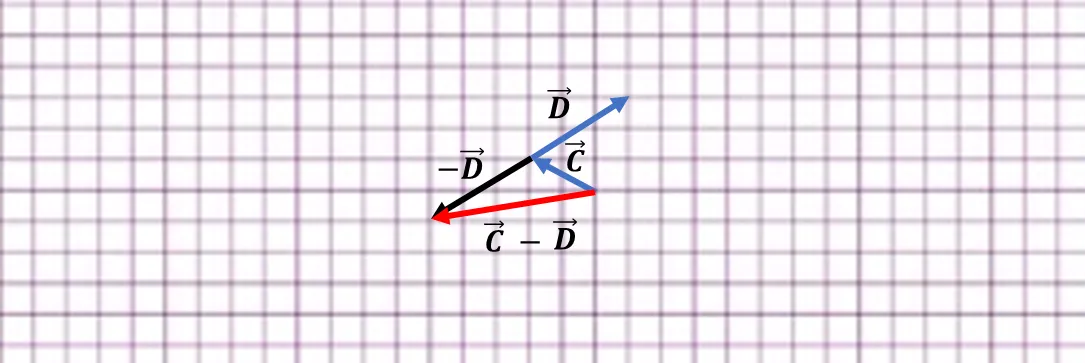
Después de graficar los vectores C y D, se procede a trazar el vector opuesto - D. El resultado será un vector cuyo origen coincide con el origen del primer vector y el extremo con el extremo del segundo vector.
Si realizamos la operación matemáticamente obtendremos que:
After plotting the vectors C and D, we proceed to plot the opposite vector - D. The result will be a vector whose origin coincides with the origin of the first vector and the end with the end of the second vector.
If we perform the operation mathematically we will obtain that:
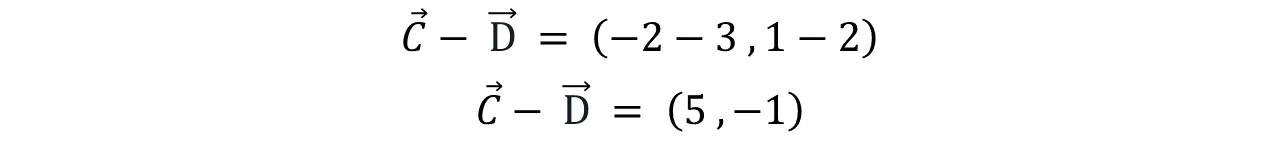
El resultado es exactamente igual al obtenido gráficamente.
The result is exactly the same as the one obtained graphically.
Producto de un número por un vector // Product of a number by a vector
Para comenzar lo primero que debemos recordar que un escalar es un número cualquiera, no es un vector. Si se considera la suma de varios vectores iguales como
To begin with, the first thing to remember is that a scalar is any number, it is not a vector. If we consider the sum of several equal vectors as
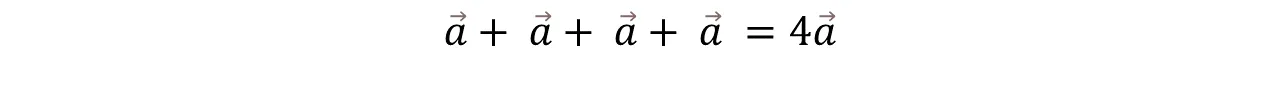
El resultado es el vector 4a, tiene la misma dirección y sentido de a, pero si módulo es 4 veces mayor. En conclusión podemos establecer que, Ka es un vector que tiene:
- La misma dirección del vector a
- El mismo sentido del vector a si k es mayor que 0.
- Sentido contrario si k es menor que 0.
Veamos un ejemplo analítico. Dado el vector A = (3,2), determine el vector 2A.
Lo primero que debemos saber es que el resultado será otro vector, cuyo sentido será el mismo que A. Cuando tenemos las componentes de un vector lo que vamos es a multiplicar dichas componentes por el número escalar.
The result is the vector 4a, it has the same direction and sense of a, but its modulus is 4 times greater. In conclusion we can establish that, Ka is a vector that has:
The same direction of the vector a
The same direction of the vector a if k is greater than 0.
The opposite direction if k is less than 0.
Let's see an analytical example. Given the vector A = (3,2), determine the vector 2A.
The first thing to know is that the result will be another vector, whose sense will be the same as A. When we have the components of a vector what we are going to do is to multiply these components by the scalar number.
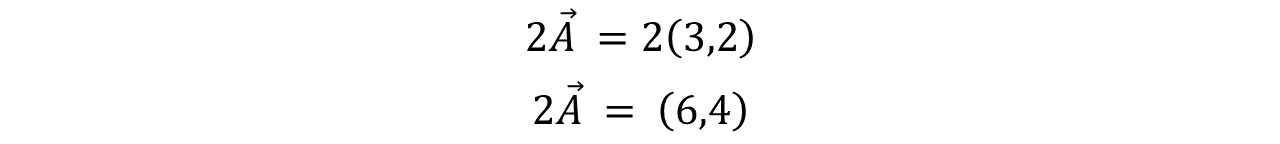
Este resultado es el vector 2A y lo podemos comprobar gráficamente así:
This result is the vector 2A and we can check it graphically as follows:
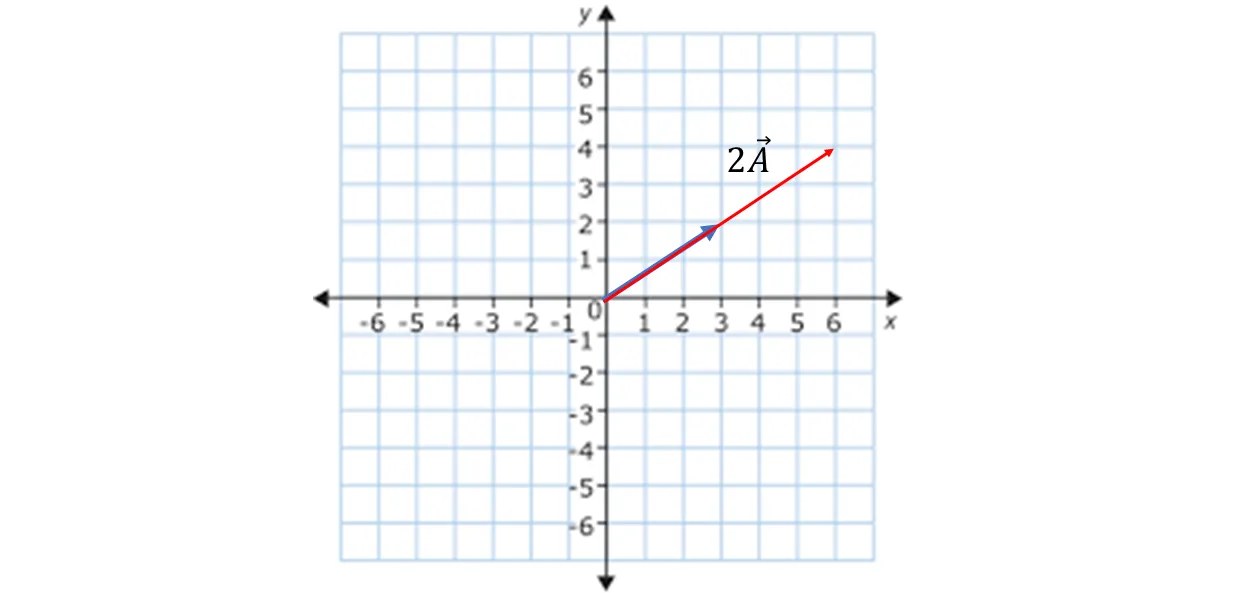
Cómo vemos el vector A es el de color azul, y el vector 2A es el doble con la misma dirección y sentido.
Ahora bien, las propiedades de la adición también aplica para la adición de vectores, veamos cuáles son:
- Propiedad Conmutativa: el orden de los sumandos no altera el resultado.
As we can see vector A is the blue vector, and vector 2A is the double vector with the same direction and sense.
Now, the properties of addition also apply to vector addition, let's see what they are:
- Commutative Property: the order of the addends does not alter the result.
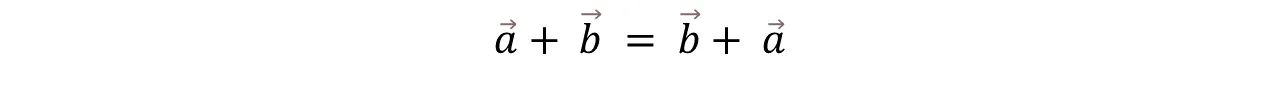
- Propiedad Asociativa: Dada una suma de tres o más vectores se pueden agrupar dos de ellos, sustituidos por el resultado de su adición y la suma total no se altera.
- Associative Property: Given a sum of three or more vectors, two of them can be grouped together, replaced by the result of their addition and the total sum is not altered.
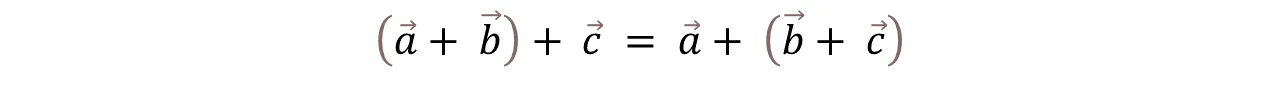
- Elemento Neutro: El vector nulo 0 es el elemento Neutro para la adición de vectores.
- Neutral Element: The null vector 0 is the Neutral element for vector addition.
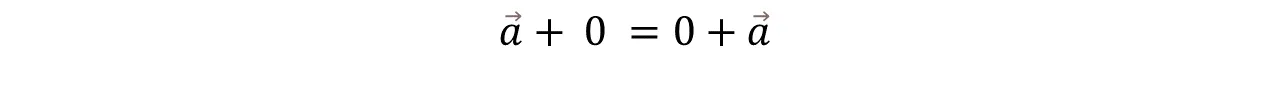
- Elemento Simétrico: Para todo vector a existe un vector opuesto -a tales que la suma de ambos es el vector nulo.
- Symmetric Element: For every vector a there is an opposite vector -a such that the sum of both is the null vector.
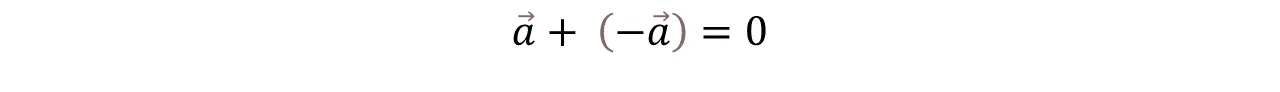
Realicemos un ejemplo: Dados los vectores a = (-3, 6), b = (5,-3), c = (½, 3/2). Realizar la siguiente operación aplicando las propiedades de la adición.
Let's do an example: Given the vectors a = (-3, 6), b = (5,-3), c = (½, 3/2). Perform the following operation by applying the properties of addition.
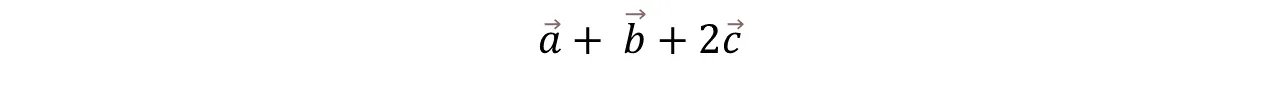
Primero escribimos las coordenadas de los vectores
First we write down the coordinates of the vectors
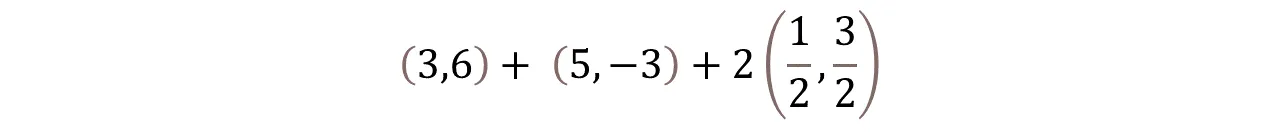
Ahora vamos a realizar el producto escalar por el vector, es decir 2C.
Now we are going to perform the scalar product by the vector, i.e. 2C.
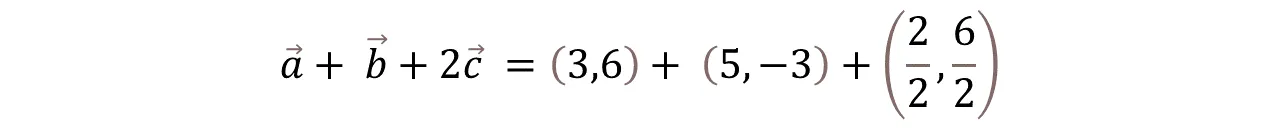
Simplificamos las fracciones obtenidas y nos queda:
We simplify the obtained fractions and we are left with:
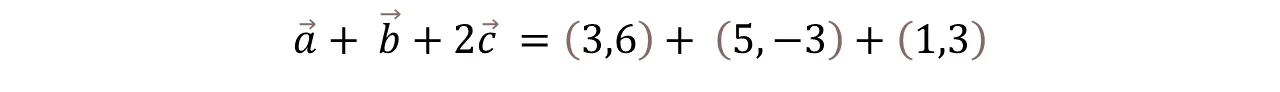
Aplicaremos la propiedad Asociativa. Dónde realizaremos a + b y el resultado que se obtenga se suma con 2C.
We will apply the Associative property. Where we will make a + b and the result obtained is added with 2C.
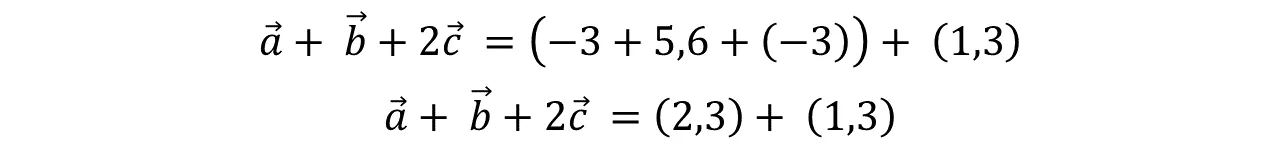
Realizamos la suma entre estos componentes.
We add these components together.
Producto punto entre dos vectores //dot product between two vectors
El producto punto o producto escalar de dos vectores, por definición, es el resultado de multiplicar los módulos de ambos vectores por el coseno del ángulo que forman.
The dot product or scalar product of two vectors, by definition, is the result of multiplying the moduli of both vectors by the cosine of the angle they form.
Es importante acotar que el producto punto entre vectores dará como resultado un escalar. Veamos un ejemplo:
Hallar el producto punto de A = (-3,5) y B = (2,-4)
It is important to note that the dot product between vectors will result in a scalar. Let's see an example:
Find the dot product of A = (-3,5) and B = (2,-4)
Si el producto punto entre dos vectores es cero, quiere decir que esos dos vectores son perpendiculares.
If the dot product between two vectors is zero, it means that these two vectors are perpendicular.
Ya para despedirme, agradezco a quienes se tomarnos unos minutos de su tiempo para leer mi publicación y me encantaría poder leer en los comentarios sus opiniones e impresiones sobre el tema.
In closing, I would like to thank those of you who took a few minutes of your time to read my publication and I would love to read in the comments your opinions and impressions on the subject.
Referencias
Baldor, A. (1941). Algebra. México, Publicaciones Cultural.
Hinds, J. (2002). Matemática 8. Caracas, Editorial Premier.
References
Baldor, A. (1941). Algebra. Mexico, Cultural Publications.
Hinds, J. (2002). Matemática 8. Caracas, Editorial Premier.
Translator Deepl

