¡Apreciados amigos de Hive Blog!
Reciban un cordial saludo.
En los circuitos eléctricos la regulación de la corriente eléctrica es de vital importancia, ya que esto permite la operación controlada y segura de los componentes y dispositivos que forman parte de la red eléctrica.
Así como las resistencias y los capacitores son elementos reguladores de la corriente eléctrica, los inductores tienen la propiedad de regular los cambios repentinos de la corriente eléctrica, por lo que son también elementos esenciales en todas las redes eléctricas.
Dada su importancia, en esta publicación obtendremos los parámetros de corriente y voltaje de un inductor con el objeto de analizar su comportamiento en un circuito eléctrico.
En nuestro análisis usaremos un inductor y una resistencia agrupados en serie alimentados por una fuente de voltaje DC, tal y como se muestra en la figura 1.
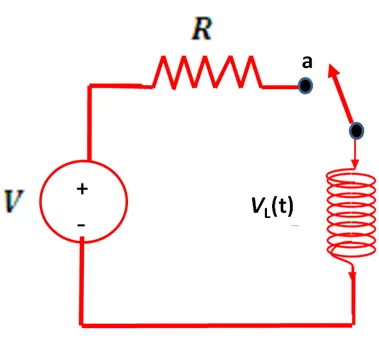
(Elaborada por @lorenzor)
En el momento en el que el interruptor se cierra, se establece en el circuito una corriente eléctrica que se incrementará gradualmente, lo que generará en el inductor, según lo establece la ley de Faraday, una fuerza electromotriz proporcional y opuesta a la variación que experimenta la corriente eléctrica, tal y como se expresa en la siguiente ecuación:
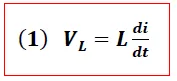
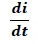→ Variación temporal de la Corriente eléctrica (A/s)
L → Inductancia ( constante de propòrcionalidad) (H)
VL → Fuerza electromotriz (Voltaje en el inductor) (Vol)
Esta oposición de la fuerza electromotriz se mantendrá hasta que la corriente eléctrica alcance su máximo valor.
Con el fin de obtener una descripción matemática de las variables corriente y voltaje en el inductor, aplicaremos en el circuito seleccionado la ley de Kirchhoff de los voltajes, tal y como se muestra a continuación:
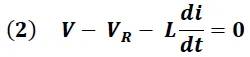
V → Voltaje de la fuente
V(R ) → Voltaje en la Resistencia
De la ley de Ohm tenemos:
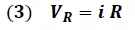
Sustituyendo (3) en (2) obtenemos:
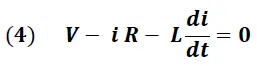
Resolviendo la ecuación (4) para determinar la corriente "i" se tiene:
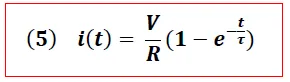
Donde
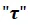es conocida como la constante de tiempo del circuito y representa el tiempo en el que la corriente alcanza el 63 % de su valor máximo y esta dada por:
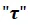es conocida como la constante de tiempo del circuito y representa el tiempo en el que la corriente alcanza el 63 % de su valor máximo y esta dada por: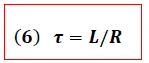
La determinación de la constante "τ " es de gran utilidad ya que permite obtener el tiempo requerido por el inductor para alcanzar su máximo valor.
La expresión (5) nos muestra que la corriente eléctrica varia exponencialmente desde su valor inicial i = 0 en t = 0, hasta alcanzar su máximo valor dado por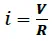 
.
.
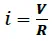Derivando la Expresión (5) se obtiene según lo establece la ecuación (1) que el voltaje del inductor es de la forma:
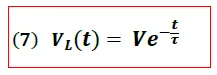
En la siguiente representación gráfica se muestra el comportamiento de la corriente y el voltaje en el inductor.
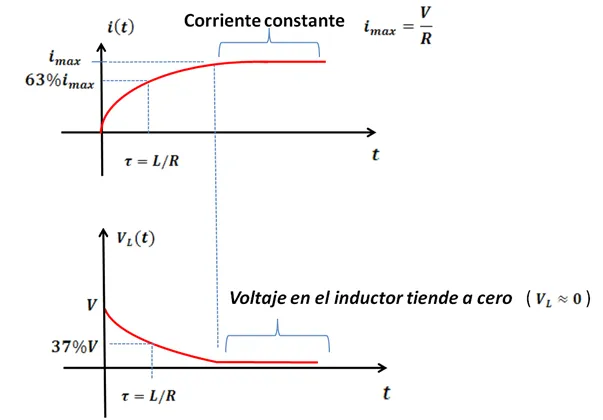
(Elaborado por @lorenzor)
De estas representaciones gráficas podemos apreciar que una vez alcanzado el valor máximo de la corriente eléctrica, el voltaje en el inductor tiende a cero, dado que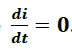 
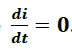
Es por esta razón que en análisis de redes los inductores, una vez alcanzado su estado estable, son considerados como un corto circuito (VL = 0).
Es importante recordar que dado que existe una proporcionalidad directa entre la corriente y campo magnético en un inductor, un máximo en la corriente implica un incremento en la energía magnética que este almacena y que regularmente es liberada en otras cargas o elementos del circuito.
Ejercicio
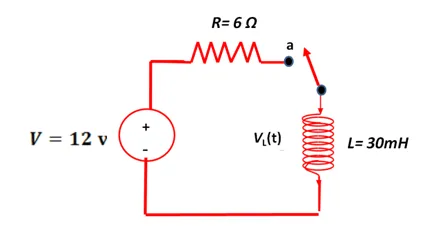
En el circuito R-L que se muestra a continuación, determine:
a) La constante de tiempo del circuito
b) Los valores de corriente y voltaje 5 ms después de conectar el interruptor.
Solución
L = 30mH
R = 6 Ω
V = 12 v
Usando las formulas obtenidas en nuestro análisis teórico tenemos:
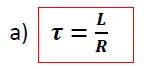
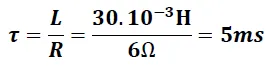
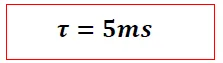
b)
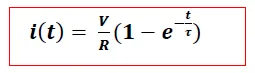
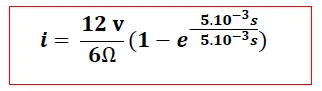
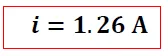
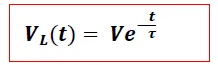
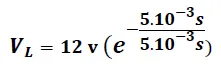
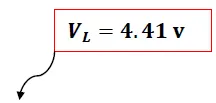
Se puede notar que en el tiempo “τ” el voltaje ya ha perdido un 63% de su valor máximo, quedando solo 37% de su valor total
( 37%)(12v) = 4.4 v
Referencias
- Circuitos Eléctricos. James W. Nilson. Cuarta edición. Addison-Wesley Iberoamericana.
- Introduction To Electromagnetic Fields Third Edition / Clayton R. Paul, Keith W. Whites, Syed A. Nasar
- Física Vol. II Campos y ondas. Marcelo Alonso, Edward J. Finn. Fondo Educativo Interamericano, S.A.
- Física para ingeniería y ciencias Vol.2 Tercera Edición / Hans C. Ohanian, John T. Markert.
- Teoría electromagnética. Willian H. Hayt, Jr., John A. Buck. Séptima edición. McGraw Hill.