Der Hammingabstand zwischen zwei Codeworten ist die Anzahl der Bitstellen, an denen sich zwei Codeworte unterscheiden. Um den notwendigen Hammingabstand zu erreichen, müssen möglicherweise redundante Bits hinzugefügt werden.
Man hat m Datenbitstellen, r Redudante Bits und somit n=m+r Codeworte. Damit können insgesamt 2^n (2 hoch n) Codeworte dargestellt werden. Die Anzahl der notwendigen redundanten Bits kann man mit folgender Formel bestimmen:
(m+r+1) <= 2^r
(m+r+1) ist eine untere Grenze für die Anzahl der redundanten Stellen, die benötigt werden, um einen Code mit m Nachrichtenbitstellen, der die Korrektur eines einfachen Bitfehlers erlaubt, zu erstellen.
Für m=7 erhält man (7 + r + 1) <= 2^r . Das kleinste r, für das diese Bedingung erfüllt, ist r = 4. Diese theoretische untere Grenze kann durch eine Methode nach Hamming [1] erreicht werden. Um einen Code mit m Nachrichtenbitstellen und r Redundanzbits zu erstellen, der es ermöglicht alle einfachen Fehler zu korrigieren, kann die Hammingmethode angewandt werden:
- Dabei werden die Bits des Codes der Länge n fortlaufend mit eins beginnend nummeriert.
- Alle Bits, die eine Zweierpotenz bilden (1, 2, 4, 8, 16, usw.) sind redundante Bits.
- Alle anderen Bits (d.h. 3, 5, 6, 7, 9, usw.) sind Nachrichtenbitstellen.
Damit wird zum Beispiel ein 7-bit Wort auf eine Gesamtlänge von 11 Bits ausgeweitet:
R1-R2-N3-R4-N5-N6-N7-R8-N9-N10-N11
Hier bedeutet R ein redundantes Bit und N ein Nachrichtenbit.
Um einen einfachen Fehler zu korrigieren werden die Redudanzbits so berechnet, dass die Parität der Bits gerade oder ungerade sind. So werden zum Beispiel für den Code vier Redudanzbits an den Positionen 1, 2, 4 und 8 benutzt. Das Redudantbit an Position 1 wird durch die Nachrichtenbitstellen an den Positionen 3, 5, 7, 9 und 11 bestimmt.
Beispiel
Der Buchstabe ’H’ hat den ASCII Wert: 1001000 (48). Wie sieht der ensprechende Hammingcode aus?
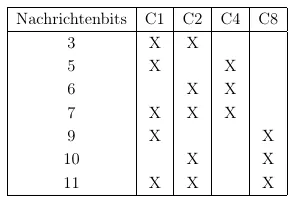
Abbildung: Tabelle zur Berechnung von Redudanzbits
Vorher : xx1x001x000
C1 = N3 + N5 + N7 + N9 + N11 = 2 (gerade Parität), daher 0
C2 = N3 + N6 + N7 + N10 + N11 = 2 (gerade Parität), daher 0
C4 = N5 + N6 + N7 = 1 (ungerade Parität), daher 1
C8 = N9 + N10 + N11 = 0 (gerade Parität), daher 0
Nachher : 00110010000
Beim Lesen des jeweiligen Codewortes wird ein Zähler mit 0 initialisiert. Dann wird jedes Bit k (k= 1, 2, 4, 8, usw.) auf den korrekten Paritätswert hin untersucht. Stimmt dieser nicht mit dem errechneten Wert überein, wird k zum Zähler addiert. Ist der Zähler nach der Berechnung aller Redundantbits null , dann war das Codewort fehlerfrei und wird akzeptiert.