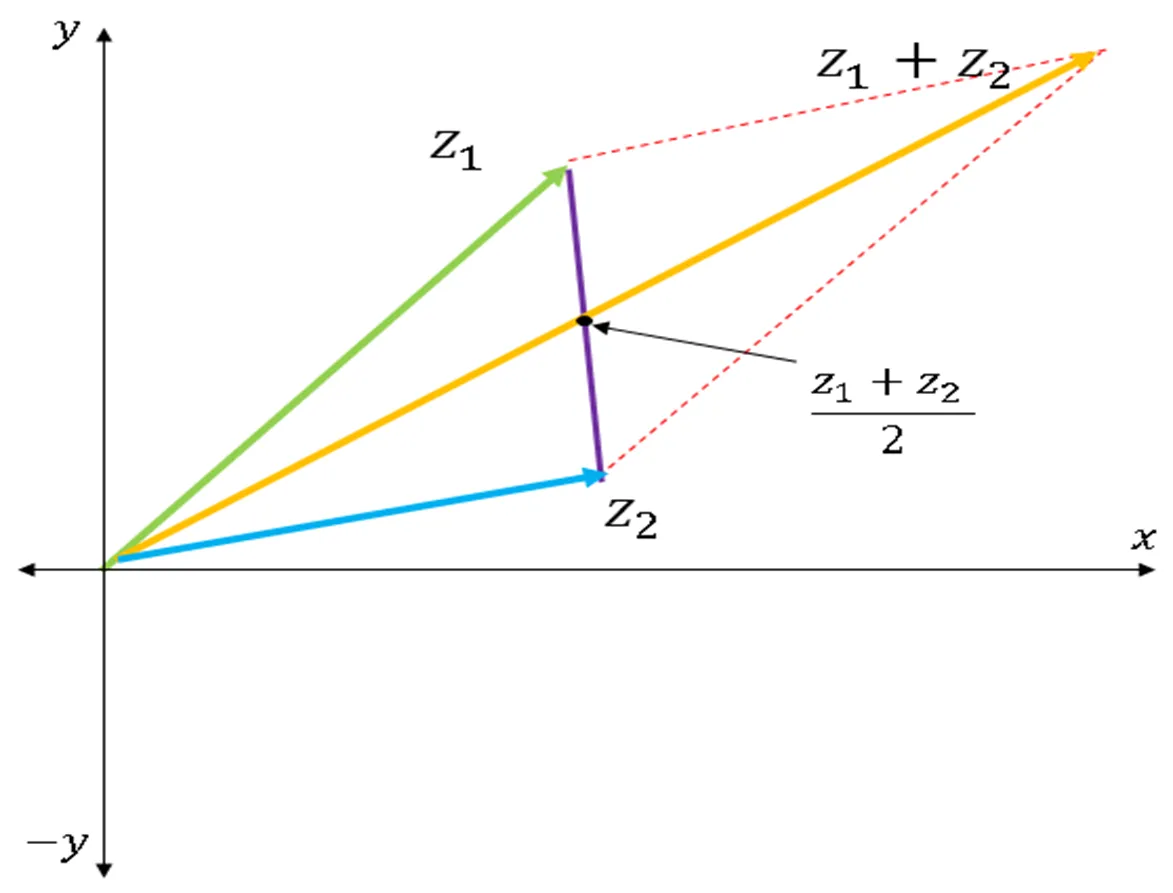
Desigualdad Triangular - Solución de problemas
Desigualdad triangular
Usando las propiedades que se expusieron en el post anterior de números complejos, (ver Fuente, podemos deducir una propiedad importante llamada la desiguialdad triangular, la cual tiene la siguiente expresión.
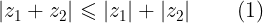
Prueba.
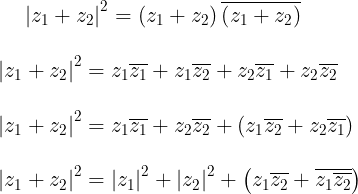
recordando la ecuación (9) del post anterior, (ver Fuente) podemos escribir
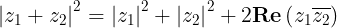
Pero por la ecuación (3a) del post antierior tenemos
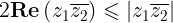
Entonces
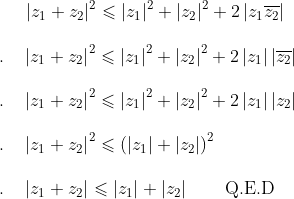
De (1) podemos extraer lo siguiente
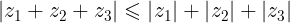
Ya que sí
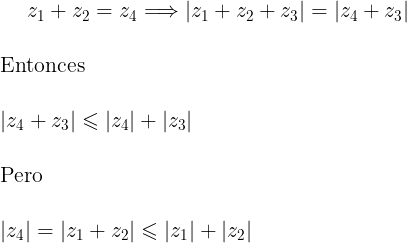
Por lo tanto
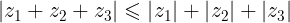
Entonces por inducción matemática podemos expresar lo siguiente
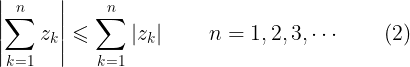
también tenemos la siguiente desigualdad
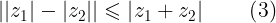
Prueba.
Sí
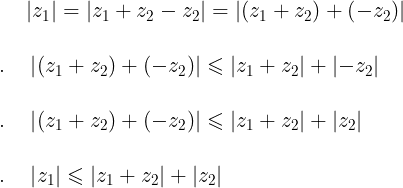
Entonces

Luego
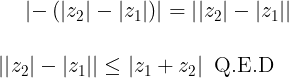
De la prueba de (3) podemos extraer dos colorarios.
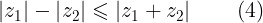
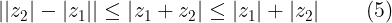
A continuación procedemos a resolver ejercicios en los que aplicaremos los conocimientos adquiridos en este post y en los anteriores.
Video 1: Demostración de la fórmula de Pascal

Video 2: Problema de inducción matemática
Video 3: Problema de ecuación de un círculo

Video 4: Problema del punto medio
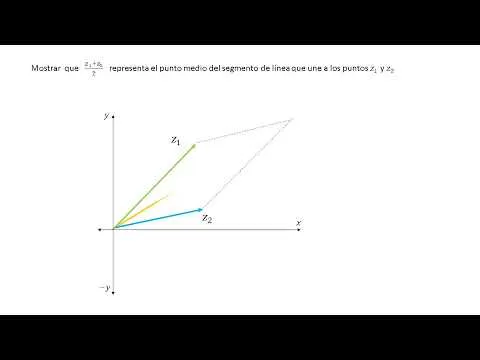
Video 5: Dos problemas sencillos
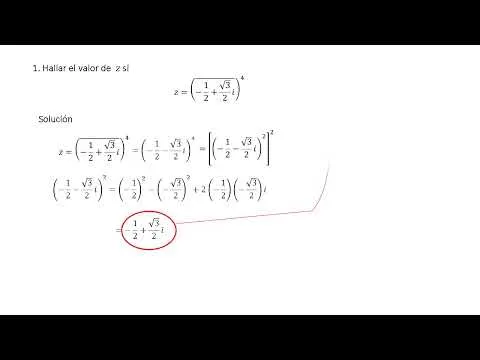
Bibliografía
- Churchill R., Brown J., Verhey R. Complex variables and applications. 3th. Ed. McGraw-Hill, New York, 1976.
- Spiegel M. Variable compleja. McGraw-Hill (Serie Schaum), México, 1971.
- Saff E., Snider A. Fundamentals of complex analysis. Prentice Hall, 3th. Ed. 2003.
- Volkovyski L., Lunts G., Aramanovich I. Problemas sobre la teoría de funciones de variable compleja. MIR, Moscú, 1984.

