Fuente
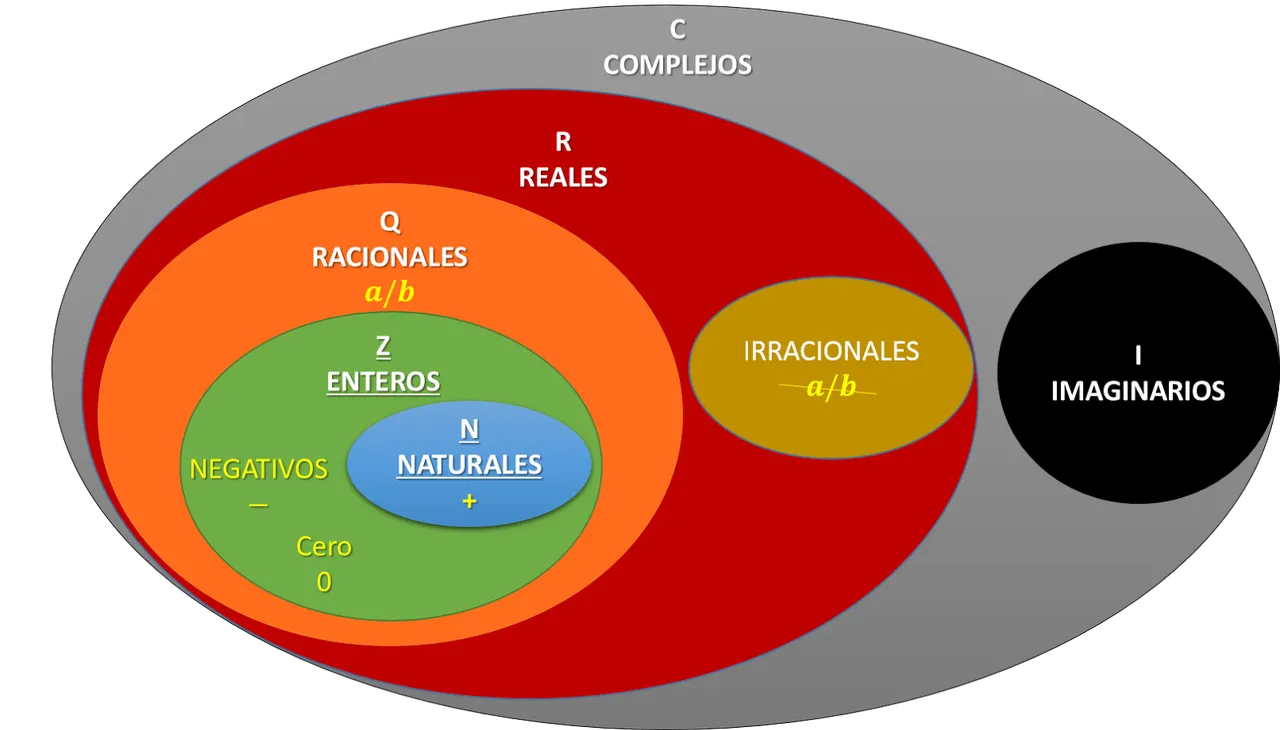
Números complejos. Definiciones
Hace algún tiempo hice un post donde explico de manera sencilla la necesidad matemática de tener una nueva clase de números, estos son los llamados números complejos, ver Fuente. Este sistema o conjunto de números, al igual que los reales, tienen una serie de definiciones, propiedades, álgebra y geometría que dan la estructura matemática para operar y trabajar con ellos.
Los números complejos tienen una gran aplicación en las físicas puras, en la ingeniería eléctrica e ingeniería electrónica. Me he motivado a desarrollar una serie de artículos en los que explicaré formalmente la teoría de los números complejos. En esta ocación comenzaré con las definiciones y operaciones básicas.
Definición de un número complejo
El conjunto de los numeros complejos lo representaremos mediante el siguiente símbolo: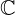 
y cada número por la letra 
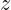y lo definiremos como un punto en el plano cartesiano, es decir, como un par ordenado
Es importante señalar que el este plano no es el plano cartesiano en sí, de hecho es el plano complejo o también llamado plano Argand, pero tocaremos este punto en otra sección.
En la ecuación (1) debemos saber que las variables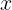 
e 
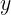toman números reales, es decir son variables reales en todo su sentido, de tal manera que los número reales son subconjunto de los números complejos
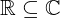
los número imaginarios puros tienen la siguiente forma:
y 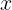e 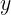son la parte real e imaginaria de 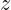respectivamente, y la notaremos de la siguiente forma
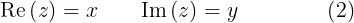
Dos numeros complejos son iguales si y solo sí sus partes real e imaginaria son iguales
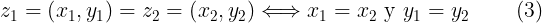
Suma y resta de números complejos
Sean los números complejos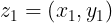 
y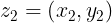 
entonces
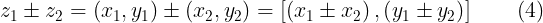
Producto de números complejos
Sean los números complejos 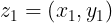y 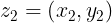entonces
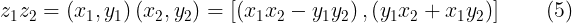
Usando (4) y (5) podemos hacer lo siguiente
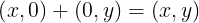
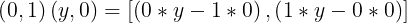
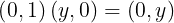
Entonces
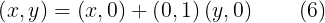
Observemos que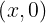 
se puede identificar como el número real 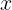, por lo tanto podemos restringir las operaciones de suma, resta y multiplicación de tal manera que obtenemos las operaciones usuales de los números reales, es decir
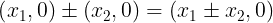
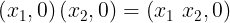
Acá, se puede apreciar con claridad que los numeros complejos son una extensión natural de los números complejos. Ahora si pensamos en un número real 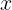o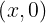 
y denotamos a 
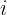como el número imaginario puro 
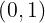, entonces podemos escribir la ecuación (7) de la siguiente manera
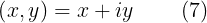
Sabiendo que
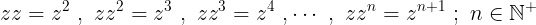
Entonces
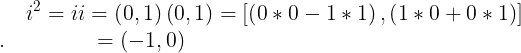
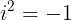
Tomando en cuenta la expresión (7), entonces podemos reescribir (4) y (5) de la siguiente manera
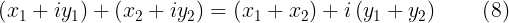
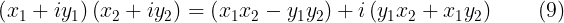
Este resultado lo podemos obtener aplicando la propiedad distributiva de la multiplicación y recordando que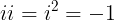 
.
Con esto terminamos la primera presentación de los números complejos, en la próxima entrega veremos sus propiedades algebraicas.
Bibliografía
- Churchill R., Brown J., Verhey R. Complex variables and applications. 3th. Ed. McGraw-Hill, New York, 1976.
- Spiegel M. Variable compleja. McGraw-Hill (Serie Schaum), México, 1971.
3.Saff E., Snider A. Fundamentals of complex analysis. Prentice Hall, 3th. Ed. 2003
