The Role of Gamma Function in Quantum Mechanics

Greetings to everyone! In the last post, we have studied normalization of wavefunction and discussed postulates of quantum mechanics. Today, we shall study a mathematical gem that plays a crucial role in quantum mechanics, that is the gamma function. Initially introduced by Leonhard Euler in the 18th century, the gamma function has found its way into various branches of mathematics and physics, with quantum mechanics being no exception.

Copy of Copy of Stemsocial ChemFam DEC (8).gif

The Gamma Function:

The gamma function, denoted by Γ(x), is an extension of the factorial function to complex numbers. It is defined for all complex numbers except for non-positive integers, where it diverges. The gamma function is expressed as:

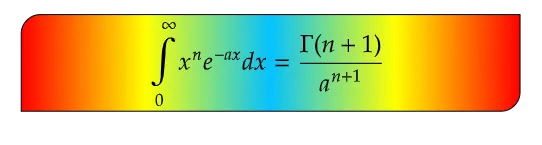
Where a is any constant. Keep in mind that this expression is valid for limits from 0 to ∞ as can be seen from the above expression.
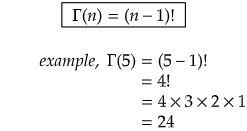
math-20240124 (1).png

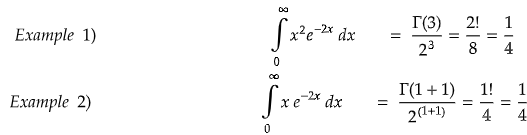
math-20240124 (2).png

Now what if the boundary limit is from -∞ to +∞ ?

In that condition, we find two values of the gamma function depending on whether the value of n is odd or even. If n is an odd entity (Number), then the gamma function value becomes zero. If it is even, we get a non zero value. For the said limits, gamma function is expressed as:

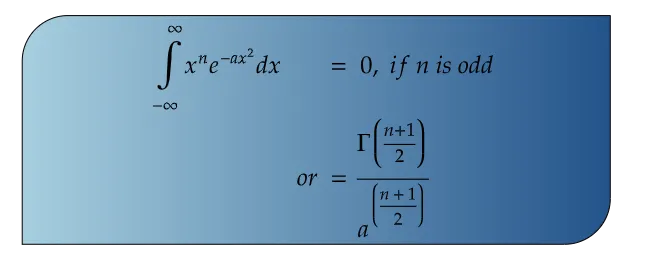
Some important gamma function values:

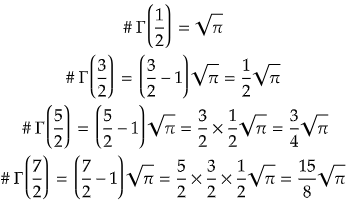
math-20240124 (3).png

This seemingly abstract mathematical construct proves to be remarkably useful in quantum mechanics, where it aids in solving complex problems involving wavefunctions, probability amplitudes, and the energy levels of quantum systems.

Quantum Mechanics and the Schrödinger Equation:

The Schrödinger equation is the cornerstone of quantum mechanics, describing the evolution of a quantum system over time. The time-independent Schrödinger equation for a non-relativistic particle can be written as:

Ĥψ=Eψ

Here,

Ĥ represents the Hamiltonian operator,

ψ is the wavefunction of the particle, and

E is the energy of the system. The Hamiltonian operator is often expressed in terms of spatial derivatives and potential energy terms. We shall discuss the Schrodinger equation in a later post, as of now, to move to the next point in gamma function, we only needed the basics. So, do not worry.

Gamma Function in Solving the Schrödinger Equation:

In certain quantum systems, the solutions to the Schrödinger equation involve the gamma function. For example, when dealing with radial wavefunctions in spherically symmetric potentials, the radial part of the Schrödinger equation may lead to equations with the gamma function.

We can show the use of gamma function while solving the radial part by taking an example.

Problem) Write the normalized wavefunction for 1D SHO (Simple Harmonic Oscillator) if,
Ψ = e^(-βx²/2) with limits from -∞ to +∞.

Solution

I hope you have not forgotten to find out the normalization constant. (Read my previous post again if so).

So, we have the normalization constant as,

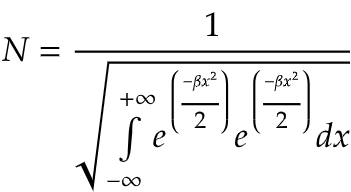
math-20240124 (7).png

Now, we need to solve the integral and find out the normalization constant.

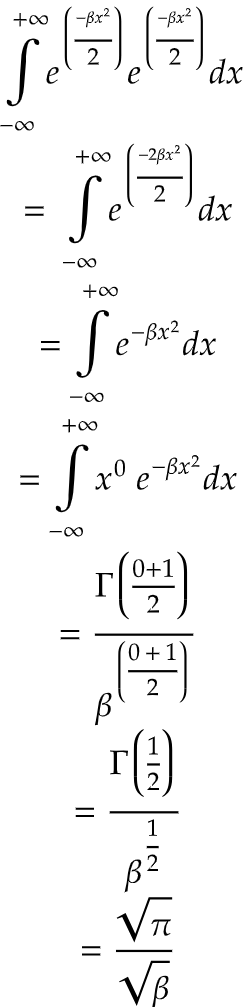
math-20240124 (5).png
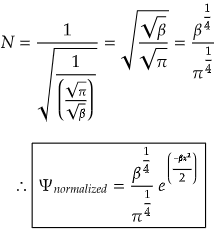
math-20240124 (9).png

Problem) Calculate the value of N if Ψ = e^-r'a₀ (0<r<∞) for H atom.

Solution

We can solve this problem by the same method as discussed above.

We have to consider only radial part as only r limit is given.
We know, volume element for radial part is,

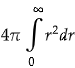
math-20240124 (13).png
Now, the normalization constant is,
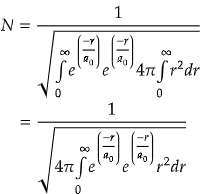
math-20240124 (10).png
On solving the integration,

math-20240124 (11).png
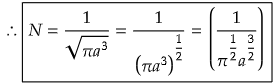
math-20240124 (12).png

What we learnt?

We studied what gamma function are and their mathematical interpretation. The gamma function, initially introduced for purely mathematical purposes, finds itself playing a pivotal role in describing the quantum world.
Discussed briefly the Schrodinger equation.
Studied the role of gamma function in solving radial part of the Schrodinger equation. The gamma function also makes an appearance when solving the Schrödinger equation for the quantum harmonic oscillator.