Parti precedenti
https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-i-introduzione
https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-ii
https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-iii
https://steemit.com/ita/@charlesx/analisi-complessa-in-pillole-iv
L'ultima volta mi sono fermato a qualche proposizione sulle funzioni armoniche, oggi vedremo alcune definizioni di base compresa quella di una 1-forma differenziale.
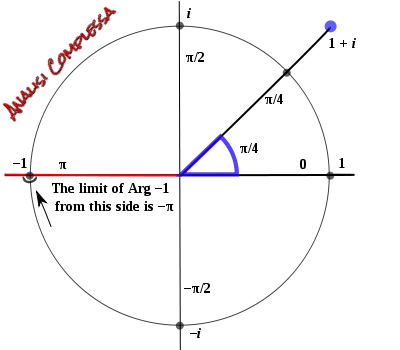
Public Domain.
Definizione: Cammino (path).
Un cammino in ℝ è una funzione continua γ: [a,b] → ℝ^2 ovvero da un chiuso al piano reale. Inoltre presi due cammini t.c. il punto finale del primo è posto uguale al punto iniziale del secondo questi possono essere intesi come un cammino solo (per esempio γ1: [a,b] → ℝ^2 e γ2: [c,d] → ℝ^2 t.c. γ1(b)=γ2(c) possono essere intesi come γ unico).
Definizione: Funzione C∞ (o liscia)
Una funzione si dice C∞ (detto c infinito) in un punto se è differenziabile infinite volte in quel punto (ovvero derivabile infinite volte rispetto a ogni variabile nel punto). Se è C∞ in tutti i punti di un insieme A allora f ∈ C∞(A) (ovvero f è C∞ su A).
Definizione: 1-forma differenziale.
Detta anche 1-forma, è un'espressione definita su un aperto U ⊆ ℝ^2 della forma:
ω= P(x,y) dx + Q(x,y) dy
con P,Q: U → ℝ funzioni C∞.
Osservazioni.
Possiamo integrare una 1-forma differenziale su un cammino γ se è C∞ e γ([a,b]) ⊆ U.
Definiamo così l'integrale:
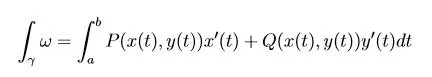
Realizzata con LaTeX base dall'autore.
L'integrale è definito anche per curve C∞ a tratti (ovvero un'unione finita di curve C∞).
Teorema di Gauss-Green.
Sia D dominio chiuso e limitato in ℝ^2 il cui bordo δD sia l'unione di curve C∞ a tratti orientato in modo che percorrendo la curva il dominio si trovi sulla sinistra.
Sia ω una 1-forma differenziale definita in un intorno di D, ω= P(x,y) dx + Q(x,y) dy .
Allora:
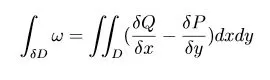
Realizzata con LaTeX base dall'autore.
Questo teorema è di fondamentale importanza perché viene usato più avanti per dimostrare risultati di una grande rilevanza.


Canali social e contatti:
Twitter: https://twitter.com/Charles73710680
charlesx@koinsquare.com
Mi trovate anche su koinsquare:
https://www.facebook.com/groups/125929638106816
https://twitter.com/koinsquareNews
Email: info@koinsquare.com
