
안녕하세요 낸드( @nand ) 입니다.
계략님이 냈던 두뇌퀴즈 선행의선행에 대해 풀이법을 공개합니다.
문제를 모르시는 분은 밑의 링크에서 문제를 읽어주세요.
- 문제: 선행의선행
풀이
처음 보고, 해적의 규칙이라는 퀴즈가 생각났습니다.
링크
많이 알려져있는 퀴즈인데, 이것도 재밌습니다.
공통점은 상대를 배려해주면서, 내가 많이 가져가야한다는거죠.
뭐든 그렇지만, 문제를 간단하게 만들면, 답은 바로 알 수 없지만,
풀이에 대한 힌트는 얻을 수 있습니다.
극과극
극과 극을 생각해보죠.
100%를 양도하면 어떨까요?
제일 처음 차례가 오지만, 얻을 건 없겠죠.
99%라면? 100%보단 좋을겁니다.
0%를 양도한다면 어떨까요?
다 얻을 수는 있지만 제일 마지막에 남은 보상만 얻어야겠죠.
1%를 양도한다면?
뒤에 0%양도자가 있다면, 그 사람보다는 좋을겁니다.
따라서 극과 극은 안좋다고 예상이 됩니다.
사이에 끼기
사이 어디에 들어가면 좋은지도 예상해봅시다.
10%와 90%에 한명씩 있다고 하고, 그 사이에 들어가야 한다고 가정하죠.
%가 안바뀌고, 이후 추가되는 사람도 없다고 가정하면,
아마도 11%만 양도하고 나머지 다 먹는게 유리하겠죠.
어떤 %가 유리한가
균등하게 분포되어 있을 때, 누가 제일 유리할까요?
귀찮으니까 컴퓨터한테 시킵시다.
일해라 컴퓨터
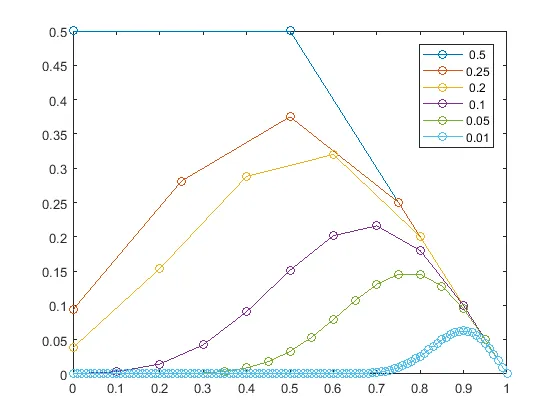
간격을 0.5에서 0.01 까지 줘가면서 다르게 계산했습니다.
결과를 보면, 간격에 따라 다르지만, 참가자6명(0.2 간격) 이상이라고 할 때, %가 반절 이상인 쪽에서 최대값이 나타나는군요.
종합
위에서 얻은 정보로 직관적으로 추론하면,
간격 중 적당히 높은%를 골라서, 사이 간격 중 낮은% 쪽으로 붙으면 되겠군요.
완전한 해법을 얻지는 못했습니다.
코드
MATLAB 코드입니다.
d_set = [0.5 0.25 0.2 0.1 0.05 0.01];
reward = cell(length(d_set), 1);
bin = cell(length(d_set), 1);
for d_iter = 1:length(d_set)
d = d_set(d_iter);
bin{d_iter} = 1:-d:0;
reward{d_iter}(1) = 1-bin{d_iter}(1);
for k=2:length(bin{d_iter})
reward{d_iter}(k) = (1-sum(reward{d_iter}(1:k-1)) )* (1-bin{d_iter}(k));
end
sum(reward{d_iter})
end
%% fig
figure(1)
plot(bin{1}, reward{1}, '-o')
hold on
for d_iter = 2:length(d_set)
plot(bin{d_iter}, reward{d_iter}, '-o')
end
legend(num2str(d_set'))
%% 는 주석입니다
d_iter의 for문은 간격에 대한 for문입니다.
for문 안쪽이 핵심입니다.
기 밑은 그림 그리는 부분입니다.
원글
읽어주셔서 감사합니다.

구독하시려면 위 마크를 눌러서 Follow 부탁드려요.
지금까지 @nand 였습니다.
아이디 마크는 @inhigh님 작품에서 발췌한 것입니다.