@rubymaker 님의 글 [rubymaker]시공간(spacetime) - 무너진 시간의 절대성] 을 읽다가 상대성 이론만큼이나 파격을 준 동시대 이론 하나를 소개해볼까 컴퓨터 앞에 앉았다. [이제 펜을 들었다 라는 상투적인 표현보다는 컴퓨터 앞에 앉았다가 대세?가 아닌가 싶다 ㅋㅋ]

아인슈타인이 시공간에서 시간의 절대성을 뒤집어 시간 조차도 상대적이다라는 것을 도입하여 물리학 이론에 변혁을 주었듯이 [자세한 내용은 @rubymaker 님의 글 [rubymaker]시공간(spacetime) - 무너진 시간의 절대성] 이러한 아이슈타인의 시공간 이론에 도전장을 내딘 사람들이 있었으니 바로 테오도어 칼루자와 오스카르 클레인이다.
아인슈타인은 4차원 시공간에서 중력과 다른 세가지 힘(강력, 약력, 전자기력)을 통합하려고 했다. 특히 그 중에서 전자기력과 중력을 통합하려고 했다. [그 당시에는 강력 약력이 잘 알려지 있지 않았다.]
이는 아인슈타인의 초기 상대론인 특수상대성이론의 핵심 가정이 멕스웰의 전자기 이론에서 시작한 것과 [빛의 속도가 일정하다 등] 더불어
그의 일반상대론의 경우에는 중력 이론을 좀 더 일반화하여 기술하기 위한 방식으로 만든 이론이기어서 그렇다.
그 당시에 잘 알려진 힘은 전자기력과 중력, 이미 멕스웰의 방정식에서 나온 대칭성 아이디어로 재미를 본 아인슈타인에게 있어 그 다음 목표는 대칭성을 이용하여 전자기력과 중력을 통합하는 것이었다.
양자역학의 아버지 중 한명이기도 한 아인슈타인은 '신은 주사위를 던지지 않는다며' 스스로 양자역학을 거부하고 그 당시 알려진 힘인 전자기력과 중력을 통합하기 위해 많은 연구를 수행한다. 중력에 다른 스칼라를 couple 하기도 하고 전자기장을 추가해보기도 하고 다른 matter 들을 넣어보기도 하고 등등등..
하지만 그의 모든 시도들은 실패로 끝이 나곤 했는데.. .그가 말년에 했던 통일장 연구에서 큰 역할을 했던 이론이 바로 칼루자-클라인 이론이다. 공개된 그의 말년 연구 노트를 보면 칼루자 클라인 이론을 이용한 통일장 이론들을 볼 수 있다고 한다..

먼저 칼루자에 대해서 이야기 해보자
나무위키에 따르면

칼루자는 아인슈타인의 시공간 이론에 감명을 받고, 다음과 같은 질문에 빠졌다.
왜 시공간은 4차원인가, 왜 4차원에 구속되어야 하는가? 우리가 너무 보여지는 것에만 집중하고 있는게 아닌가, 보이지 않는 숨겨진 차원이 있으면 어떻게 될까?
이에 칼루자는 흔히 말하는 metric 에 vector potential 을 도입해서
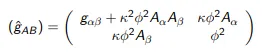
5차원에서 4차원의 중력과 전자기력을 통합하는데 성공하였다.
다만 이 이론을 통해 계싼한 전자의 전하량 값이 너무나도 안 맞게 나와서...
또 칼루자는 이 여분의 차원에 대한 해석을 하지 못했기에
특히나 왜 이런 여분의 차원을 볼 수 없었나에 대한 답을 내지 못했기에....
[여담으로 칼루자의 성격에 관한 이야기를 하나 하자면 ㅋㅋㅋ
아주 잘 알려진 일화로 칼루자는 책으로만 수영을 배운 것으로..
이론만 알면 응용, 실전은 금방한다고 믿는 사람이었다.
실전에선... ㅋㅋㅋㅋ]

몇년 뒤 클라인이 여기에 대한 답을 낸다.
클라인은 이러한 여분 차원이 매우 작아서 볼 수 없고, 이러한 작은 차원은 주기성을 띄고 있어 푸리에 전개를 통해 전하와 질량을 양자화 할 수 있다는 것을 보였다.
이러한 결정적인 것들을 했기에 칼루자 이론이 아니라 (물론 칼루자 이론이라고 부르는 사람들도 있지만) 칼루자-클라인 이론이라고 불리며 새로운 패러다임의 변환을 주는가 했는데...
양자역학, 양자장론으로 인해 표준모형이론이 각광받으며 한때 거의 사장되기 싶히 하다가, 초대칭 이론의 등장과 초창기 끈이론의 성립 과정에서 이 extra dimension 은 엄청난 역할을 하게 된다.
여기서는 칼루자와 클라인의 5차원에서 더 나아가 여분 차원이 1개가 아닌 더 많은 차원으로 간주하고 이론을 풀어나가는데, 이러한 여분 차원은 매우 작은 차원으로 간주되는 등, 클라인의 해석이 통용된다.
최근(?) 에는 리사 랜들과 선드롬의 RS 모델로 이러한 extra dimension 을 이용한 현실 물리를 보는 모델들이 각광(?)을 받고 있다.
리사 랜들의 나무위키 일부를 캡쳐하는 것으로 마무리 한다.

다음에 기회가 된다면 이러한 여분 차원의 수학적 구조에 대해서 이야기를 해 보고 싶다 ㅋㅋㅋ 칼라비 야우의 수학적 구조에 대해서 다루고 싶긴 한데..
여담으로 여분차원에 관한 괜찮은 대중과학서 하나를 소개하는 것으로 이번 글을 마무리한다.
바로 폴 핼런의 그레이트 비욘드

칼루자와 클라인 이론의 역사적인 배경들과 각각 학자들의 이야기에 대해서도 다루는 몇 안되는 책 들 중 하나이다. [대부분의 대중과학서들은 칼루자 클라인 이론을 아주 간략히 설명하고 넘어가곤 하는데 이 책은 칼루자와 클라인 각 개인의 삶과 이론들에 대해서도 비중을 좀 두고 있는 그런 책이다. ]
뭐 솔직히 여전히 이런 extra dimension 을 도입하지 않고 4차원 물리를 이용하여 통일장을 기술하려는 시도가 있다.[많지는 않다.] 지금은 extra dimension 생각이 대세이지만.. 또 언제 패러다임 변환이 일어날지 우리는 알지 못한다.