흔히 고전역학을 배우고 양자역학을 바로 배우는 학생들 중에서 몇가지 쉽게 착각하는 것이 있다. 이번 포스팅에는 그 중 하나를 이야기 해 보려고 한다.
바로 commutator 와 poisson bracket 이야기이다. 먼저 각각에 정의를 알아보자
commutator 는
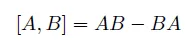
만약 A,B 가 실수라면 commutator 는 자연스럽게 사라지고 무의미해진다. 양자역학에서는 이러한 operator 들이 실수가 아니라 행렬로 존재한다. 그러기에 우리는 양자역학을 행렬역학이라고 부르기도 하는 것이다. 즉 양자역학에서 A,B 는 행렬이기에 일반적으로 저 commutator 값은 0이 되지 않는다.
반면에 푸아송 브라켓은
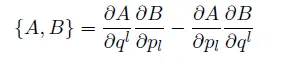
이런 형태를 가지는데, 여기서, p,q 는 single-valued 값을 갖는 함수 이기에 pq=qp 를 만족하여 commutator 처럼 단순히 순서를 바꾼 차로 정의하면 무의미한 값을 준다. 그래서 저런 미분 형식으로 정의한다. 이 푸아송 브라켓은 거꾸로 어떤 특정한 조건을 만족하는 방정식의 해로써도 구할 수 있는데 한번 계산 포스팅 거리로 준비해서 올려 보도록 하겠다.
아무튼 commutator 는 양자역학을 Poisson bracket 은 고전역학을 기술하는 operator 로 각각 Hamiltonian 과 다른 operator 를 취했을 때, 그 시스템의 시간의 변화율을 의미한다는 공통점이 있다.
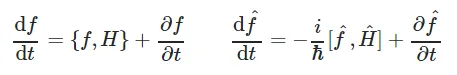
[양자역학에서는 operator 의 의미로써 특별히 기호에 모자를 입힌다. (hat 을 쓴다 ㅋㅋ) ]
더 나아가 일반적인 교과서에서도 항상 다루듯이
양자역학의 기본상수인 hbar 의 특정 리밋을 취했을 때 푸아송 브라켓과 commutator 형태로 인해
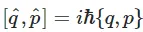
이걸로 그냥 푸아송 브라켓이랑 commutator 가 특정 극한에서 같구나 하고 넘어가기가 쉽다.
물론 1st order 에서는 맞는 이야기이다.
즉 저 식을 사실 엄밀하게 쓰자면 다음과 같이 쓸 수 있다.
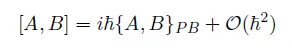
왜 이렇게 쓰느냐 [q^i, p^j] 이 값을 구할 때 함부로 저런 limit 을 취할 수 없기 때문이다.
한번 {q^2, p^2} 을 구해보자
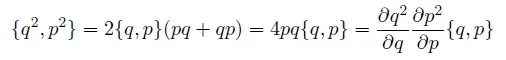
여기서, q,p 는 qp=pq 이기 때문에 저런 식으로 쉽게 정리가 된다.
하지만 양자역학에서는 그렇지 못하다. 살짝 notation 을 바꿔 보자, 일일이 hat을 넣어 타이핑하기 귀찮기에 a와 bar a 를 도입해 보자. (사실 이것이 양자역학에서 말하는 ladder operator 이다)
특별히
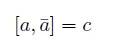
여기서 c 를 c-number 즉 operator 가 아닌 어떤 숫자 값을 의미한다. commutator 의 Leibiniz rule 을 이용하면 쉽게
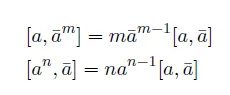
를 보일 수 있다. 조금 더 나아가면
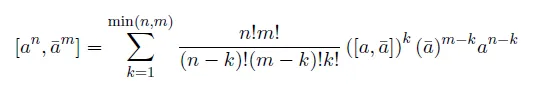
[사실 이 식을 바로 보이는 것은 조금 어려울 수도 있겠다. commutator 이전에 두 ladder operator 의 곱을 바꿔 쓰는 방법을 생각해 보고, a^2 \bar{a}^2 경우를 생각해 보면 어느정도 일반화 할 수 있다. 후에 Field quantization 소개 같은 포스팅을 하게 되면 그 때 자세히 다루어 보도록 하자.]
앞에와 마찬가지인 경우를 해보자
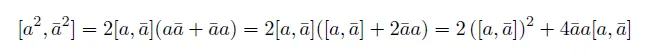
실제로
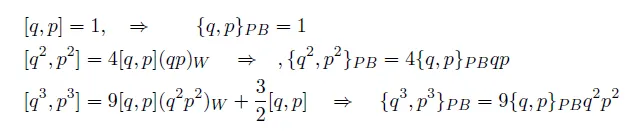
여기서 W 는 weyl ordering 을 말한다. 뭐 이런 commutator 계산은 장론 계산에서 normal-ordering 으로자주 등장하게 되며 계산 결과의 물리적 의미와 연관되어 있다.
아무튼 하고 싶은 말은 higher term 들이 있기에 일반적으로 함부로 poisson bracket 과 commutator 를 동치시켜서는 안된다. [뭐 그냥 [x,p] 정도만 생각하면 사실 위처럼 힘들게 생각할 필요는 없긴 하다. ]
같은 맥락으로 양자역학의 기대값과 고전역학의 운동방정식을 연결해주는 Ehrenfest theorem 도 학생들이 착각하기 쉬운 예 중 하나이다.
일반적으로 고전역학에서 성립하는 p=mv 와 F=ma 와 같은 식들의 양자역학 버전은 다음과 같다.
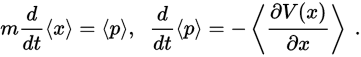
이로 마치 고전역학에서 등장하는 여러 수식들이 전부 저런 형태로 적힐 것이라는 착각을 종종 하곤 한다.
사실 이는 매우 특별한 경우에 성립하는 것이고 실제 일반적인 operator 에 대해서는

즉 x와 p 가 매우 특별한 것일 뿐이다. ([x,p]=1!!!!)
위 식을 증명하는 것은 매우 쉽다. 학부 양자역학 수업에 꼭 다루는 내용 중 하나이고 앞에 링크를 단 에렌페스트 정리에 증명 과정이 나와 있다. 그냥 기대값에 대한 미분을 할 때 미분의 분배버칙을 잘 이용하면 된다.
아 근데 잠깐만? 저 식 어디서 본 식이 아닌가? ㅋㅋㅋ 맞다 맨 처음에 서술한
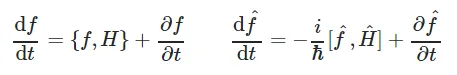
식이랑 같다. 고전 역학에서 이 식은 리우빌 정리와 해밀토니안과 연관되어 있고, 이를 그대로 차용해 양자역학화에서 시스템의 dynamics를 보는데 쓰인다.
이토록 양자역학과 고전역학은 구조적으로 많이 닮았지만[ㅋㅋ 사실 닮을 수 밖에 없긴 하다 ㅋㅋㅋ] , 실제 계산 결과는 서로 다른 결과를 준다. [양자역학적 계산 결과의 보정 텀들이 우리의 세상을 바꿨다. ] 신기하지 않은가? ㅎㅎ