By following previous post , in this post we will show the rest terms are equivalent.
Recall that
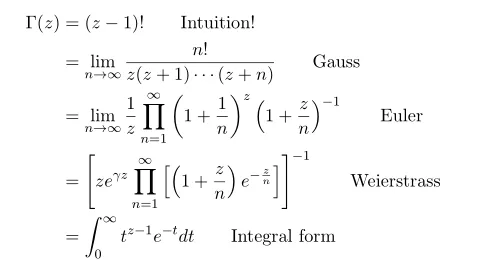
and in the last posting we have shown that expression of factorial, Gauss and Euler are equivalent to each other. In this post we will extend this to Weierstrass and integral form.
Weierstrass
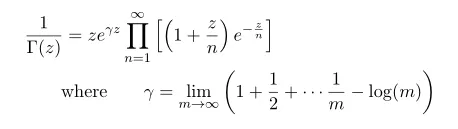
Thhis expression contains Euler constant gamma, so this definition is powerful when we encounter di-gamma and poly-gamma function.
For this Weierstrass gamma function we will show that this expression is equivalent to Euler form.
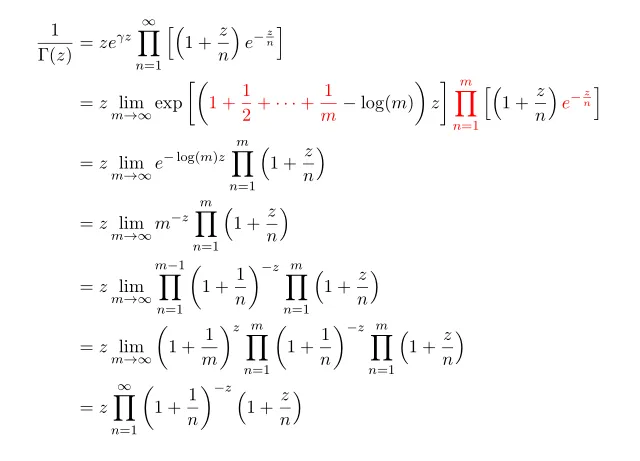
In the process we used
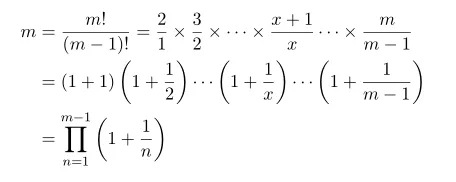
Integral form
This is the most well-known expression for gamma function.
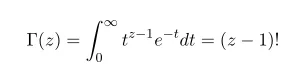
For Re(z)>0, by integration by parts we can easily see that this expression is equivalent to the Factorial.
But this is not funny, so by little deformation check the equivalence to other version of gamma function.
First slightly deform the gamma function as
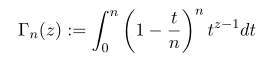
of course this is well-defined on Re(z)>0
By Integration by parts
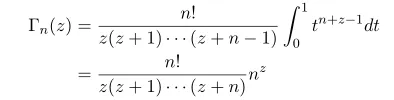
take n to infinity we can see that this function is actually the gamma function.
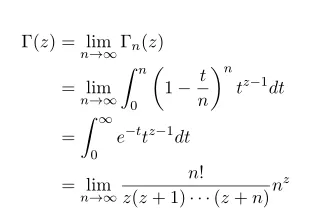
Thus the integral form of gamma function is equivlanet to the Gauss version of gamma function.