
In my previous posting on Riemann geometry [math,computation] Riemann geometry: Ricci scalar written in metric explicitly we express Ricci scalar in terms of metric only. In this post we will express Ricci curvature in terms of metric only.
Starting from the defintion of Ricci curvature
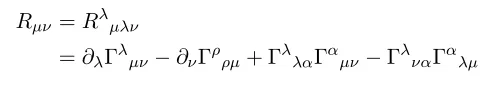
The interesting fact about Ricci-curvature is that it it symmetric under exchange of mu,nu. [We can prove this via the property of Riemann curvature tensor]
Now let us recall the expression of Riemannian connection
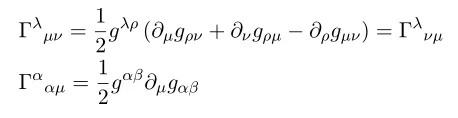
By plugging this to the formula and re-orgaanize we have
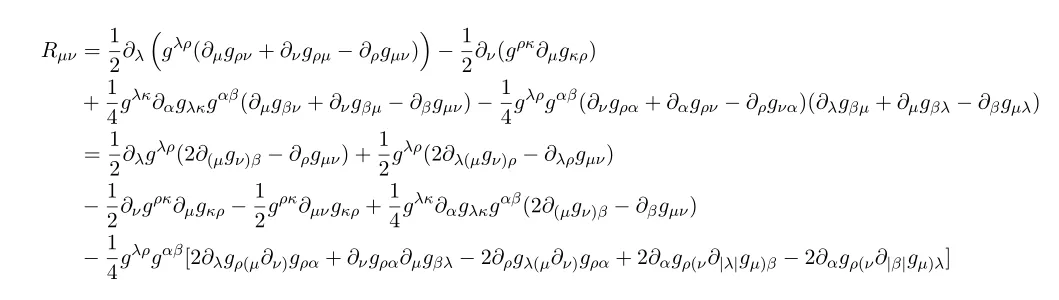
The reason why I didn't just expand the first line but write it as a second line is to show the symmetric properties of Ricci curvature explicitly. Note the expression on (,) notation means
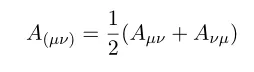
here factor 1/2 means the normalization of two.
Now let us back to the above long expression. For the first line to the second line we used following equation
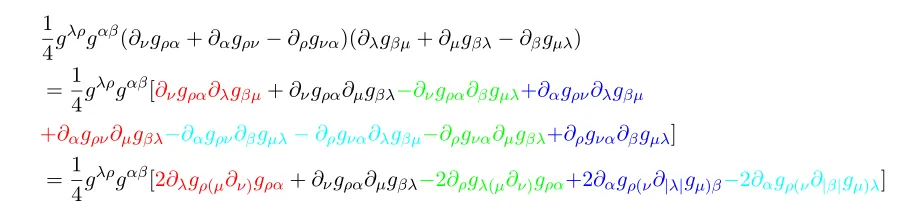
For matching up colored terms we re-label the dummy index and use the symmetric properties of metric which contracted with.
To check symmetric properties, let us decompose and see the results again
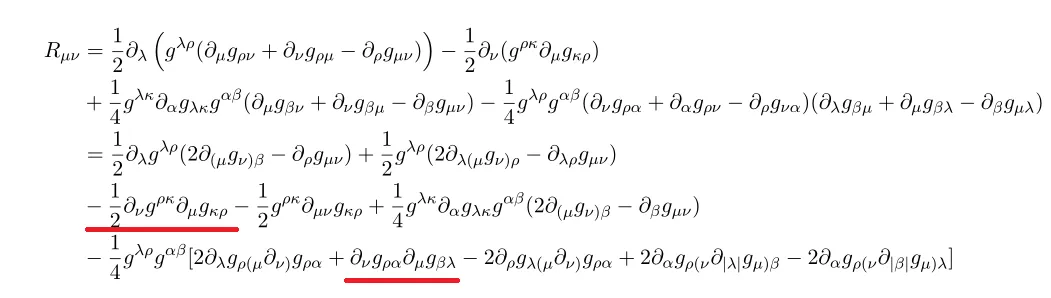
Except red terms we can easily see the symmetric properteis between exchange of mu,nu.
The symmetric properties of red term can be revealed from this equation

Now we are done.
And again by contraction with metric g^{\mu\nu}, the computation are same in [math,computation] Riemann geometry: Ricci scalar written in metric explicitly and obtain the same Ricci scalar expression