
Continuing on previous posts on affine connection, In this posting we will cover why we called above connection as affine connection.
First review,
affine connection satisfies
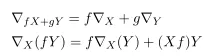
In a coordinate basis, affine connection can be defined as
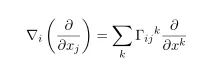
and in a coordinate basis, vector can be defined as
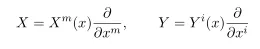
Thus
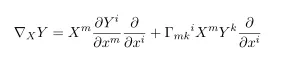
Under special case such as this connection vanishes we can write

In coordinate transformation such as 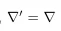
is called affine transformation.
This is due to
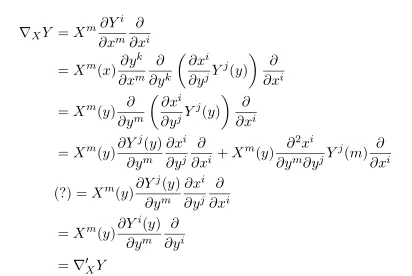
where in the process we used

Note that Ax+B is a affine transformation, so that's the reason why we called this connection affine connection.
Furthermore, In Riemannian geometry, such coordinate basis which connection vanishes called Riemann normal coordinate(RNC).
We can do the same thing via last posting
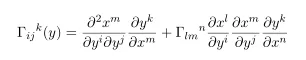
with connection vanishes and solve the equation.