
In this posting, we will derive some transformation law of connection. Thus see that this connection is not tensor but its anti-symmetrized transforms as a tensor.
In this posting, we will not directly cover Riemanian connection but we will cover more generalized version, affine connection.
First,affine conection, nabla satisfies following things
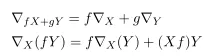
Here f and g are scalar function and X,Y are vectors.
In particular, for coordinate basis we can define affine connection as follows
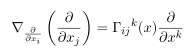
The reason why this is called affine connection will be main topic in upcoming post.
Transformation law
In general for coordinate transformation we have
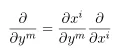
This is nothing but a chain rule.
Using this we have transformation rule for (p,q) tensor as follows
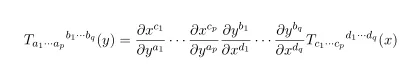
On the other hand it turns out that transformation rule for affine connection is
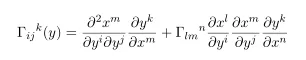
thus we see that connection is not a tensor.
Now let's derive the transformation rule for connection.
First in y basis the affine connection can be defined as
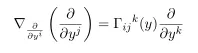
Thus
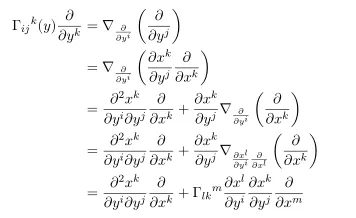
contracting y^l both sides and re-organizing dummy variables we have
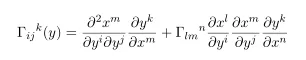
Now let see the symmetry. In Riemannian connection, the lower two index have symmetric property but for this affine connection we don't.
Thus for the affine connection, their transformation law for the first term is symmetric under i,j but the second term does not. Thus we can anti-symmetrized and obtain
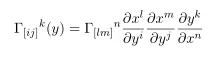
Thus the anti-symmetrized parts transform as a (2,1) type tensor. This is called torsion. Note in Riemannian geometry, since the Riemannian connection has symmetric properties on lower indices, their torsion is zero.