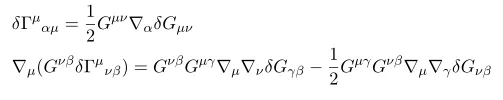In my previous posts, I have been writing posts about Riemann geometry. Today I want to talk about variation in Riemannian geometry and further take one exercise, obtaining equation of motion of Low-energy effective action of string or super-gravity theories. Actually I think the most simple example of this kinds of variation in physics is Einstein-Hilbert action. But they are already well explicitly done in many other general relativity textbook. and even in Wikipedia
So little bit detour I came up with this action and do the variation to obtain equation of motion.
First in string frame, Low-energy effective action is given as follows
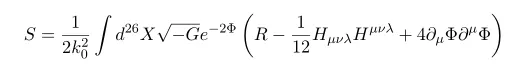
We can define beta function which is related with equation of motion for corresponding variables as follows
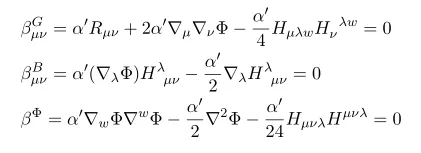
The purpose of this and subsequent post is to derive these equations of motion.
Usually we encounter these equations in string theories super-gravities, and recently you can see this in phenomology etc
Required equations
To proceed we need following formulas
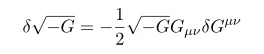
For showing this you need some background on determinant and trace property and some computation
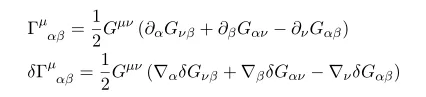
To showing this you need some computation
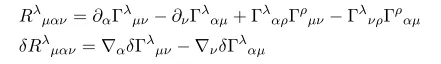
Showing this is easy, just expand covariant derivatives
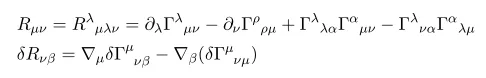
using the formula above, variation of Riemann tensor, you can directly obtain the variation of Ricci tensor.
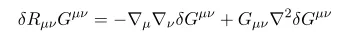
This requires some computation
Now let's compute and show the detail process
About metric G
First consider the following relations
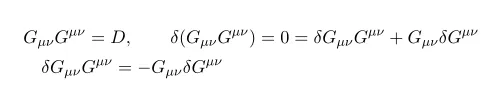
Here D denote dimension which is constant. The second line is important result.
and
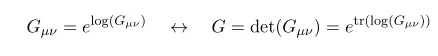
which is nothing but a relation between exponential and log, and trace and determinant relation. For the second one by taking eigenvalues (i.e., diagonalization, you ccan easily show the tr-det formula)
equipped with these materials we can compute the variation of G which is determinant of metric G_{\mu\nu}
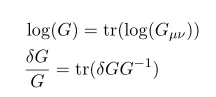
here we used
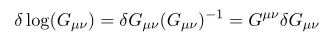
Combine all we have
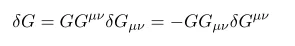
Note considering phyics sides, since they treat space and time with different signs for computing determinant it demand extra - sign. So to make it positive we need extra - sign inside square root
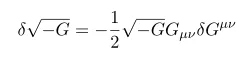
variation of Connection
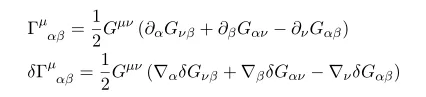
Explicit computation shows
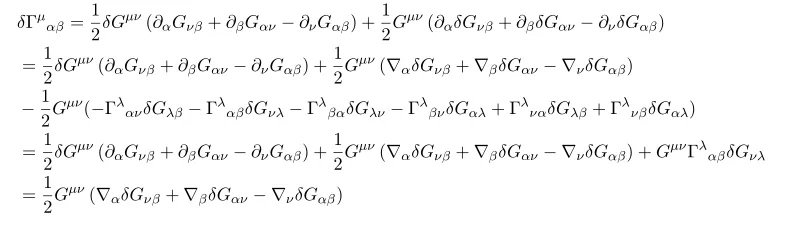
In the process we used
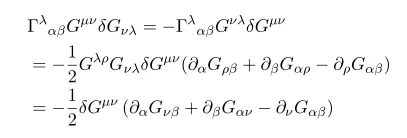
For the variation of Riemann tensor and Ricci tensors are nothing but expanding of covariant derivatives so I skipped. But for this equation
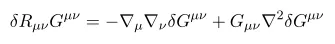
we need some computation.
Computing explicitly,

In the process we used