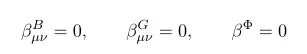In the last posting, we derive some equations. Using these results as an exercise let's compute the equation of motion of low-energy effective action of string theory.
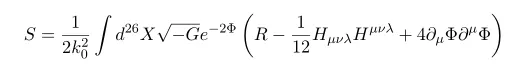
The equations of motion are following
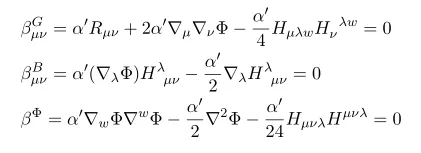
Note H=dB which is totally anti-symmetric (note B is two form, anti-symmetric which we called Kalb-Ramond two form)
Variation of B
Let's do variation about B
Before that recall the definition of H
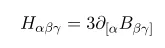
Simply one can write H=dB, and since B is two-form, anti-symmetric, we can write H explicitly as follows
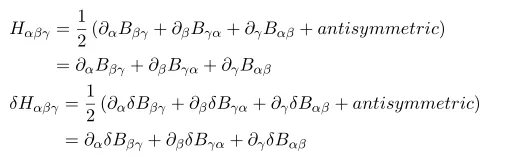
Now do the variation
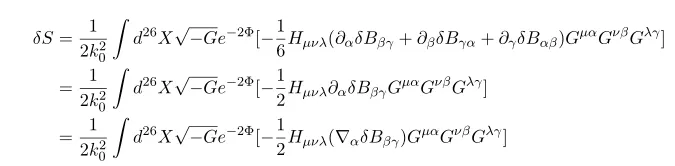
First parts comes from variation of H^2 and the second part we used
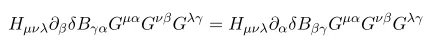
and the last line we used
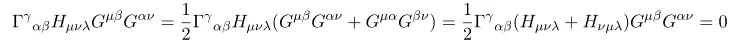
Here we used the symmetric properteis of Connection and totally anti-symmetric properties of H
Thus
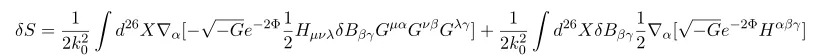
via
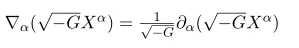
up to total derivatives
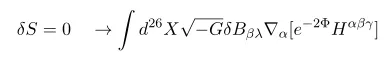
Thus we have

Variation about scalar Phi
Variation about scalar Phi we have
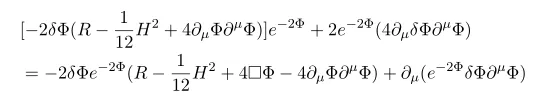
Here we used

Checking in terms of action
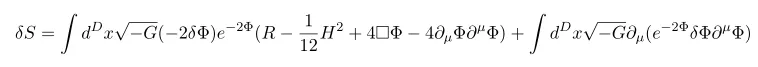
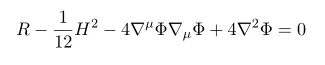
Recall the definition of beta function
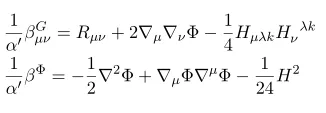
which is nothing but
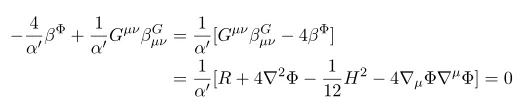
Thus
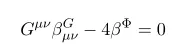
Variation about metric
First do variation about metric G
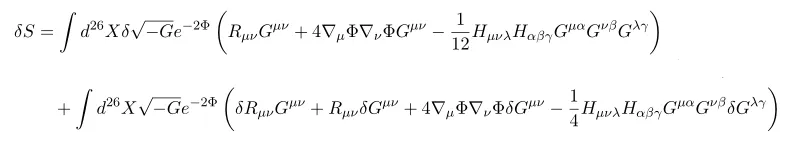
To obtain this equation we used
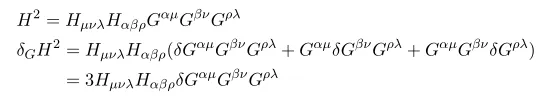
and
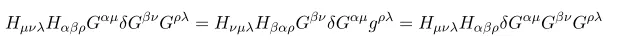
To proceed the computation using following equations
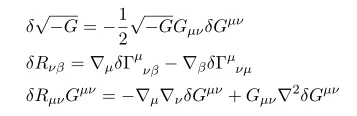
Specially
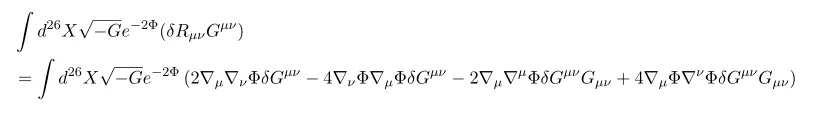
In the process we used following equation with vanishing total-derivatives terms
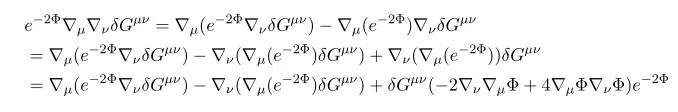
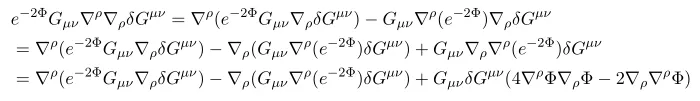
Now combing results we have
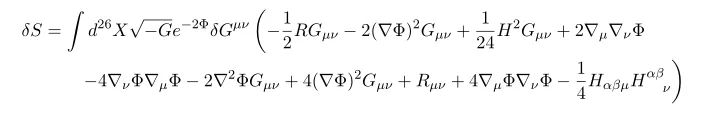
Thus
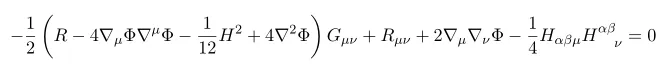
The first equation is nothing but equation of motion for Phi. Thus recall the definition of beta function we have

summary

By solving linear equations we have