Hi there. In this post, I want to share my thoughts on how it is difficult to make mathematics "fun" in higher level mathematics.
It is well known that math is difficult and time consuming. When it comes to math education, there is a lot of material out there in trying to make mathematics fun. Trying to make math fun for students keeps them engaged in the subject. A few problems with this is that by nature math does require lots of work for understanding. There is a point where math is no longer considered "fun". For many, math no longer becomes "fun" and becomes more of a chore when there are fractions, unknown variables such as x, functions, math notation, and math proofs.

If You Can't Make It Fun, Try To Make It Interesting
Since higher level mathematics is more theoretical, structured and more abstract, it is very hard to make math fun. The next best alternative is to make mathematics interesting. Whether the mathematics is pure math or applied math, math educators (professors in particular) should try their best to teach the material well and state the importance of the topics being taught.
Making courses interesting is much easier said than done. High school mathematics courses get more structured and more theoretical with the algebra, symbols, logic and problem solving. Mathematics courses at the university level are typically taught by professors who at least a Masters or PhD degree in the subject. The teacher's degree is a factor but it is not the only factor. Good communication skills on top of subject knowledge helps students understand course material better and keeps them engaged.
Do note that there are students who will not find certain subjects/topics interesting no matter how much the teacher tries. You can't force things.
A Few Examples
Example One
There is a lot if skepticism when it comes to algebra. Some would ask questions such as "When would I use this?". One way of trying to make math interesting is pointing out that learning algebra helps in understanding structures, understanding rules and working within rules. Algebra is like a language and trying to understand algebra is like learning a new language.
One algebra example is the order of operations a.k.a BEDMAS.
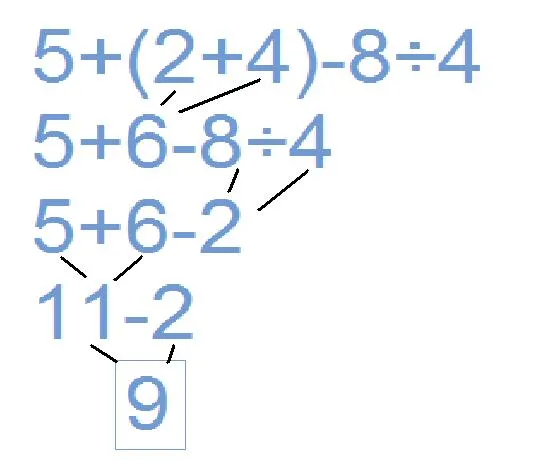
Example Two
In university level mathematics, it is important for math students to be able to do math proofs. Some places may have an introduction to math proofs course or some sort of prepositional logic type course.
It takes a lot of time and mental effort to be able to understand and write math proofs. As one gets better in math proofs, the logic and (critical) thinking skills improve over time. The contents in pure math courses may not have much (industrial) applications but gaining thinking skills is very useful for math and in life.
