
Francois Viete, for whom the topic of this post is named. Source: Wikipedia.org, Public Domain
François Viète was a French mathematician who worked in the 16th century, and one of the earliest to combine classical Hellenistic techniques with the then-novel techniques of Algebra introduced from the Arab world. He worked as a lawyer and as an adviser to Kings Henry III and Henry IV of France [1], nut is perhaps best known today for the set of formulæ that bear his name, called "Vieta's Formulæ". Vieta's formulæ are a set of rules that relate the coefficients of a polynomial to the roots.
The Quadratic and Cubic Cases
Let us consider the function
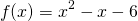 . It is clear, even to younger students, that this expression can be factored to
. It is clear, even to younger students, that this expression can be factored to 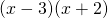 , yielding the roots
, yielding the roots 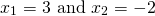 . Multiplying the two roots gives us
. Multiplying the two roots gives us 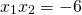 and adding them gives us
and adding them gives us 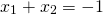 . These are the same as the coefficients of the quadratic function (-1 and -6). This should not be very surprising given that, by the FOIL method, we might write
. These are the same as the coefficients of the quadratic function (-1 and -6). This should not be very surprising given that, by the FOIL method, we might write 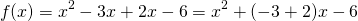 . In fact, it can easily be shown, using the quadratic formula that, for
. In fact, it can easily be shown, using the quadratic formula that, for 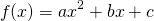 , if
, if 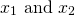 are solutions, then:
are solutions, then: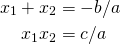
The proof of the above involves only elementary algebra, and will be left to the reader.
If we consider a cubic case such that 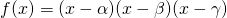 , it's obvious that the zeroes of this function are
, it's obvious that the zeroes of this function are 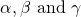 . If we re-write the function by expanding it, we obtain:
. If we re-write the function by expanding it, we obtain:
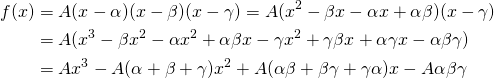
And equating coefficients so that
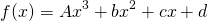 , we can write the following:
, we can write the following:
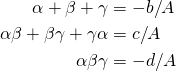
Vieta's Formula for Higher Powers
Now, our goal should be to extrapolate the patterns for higher powers. We might guess, based on the pattern that the coefficients can be deduced by multiplying and adding the zeroes. To do this, we first introduce the elementary symmetric sum:
The k-th elementary symmetric sum of a set of n elements is the sum of all products of k elements - without repeating an element - from that set.
For example in the cubic case,
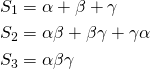
And in the quartic case:
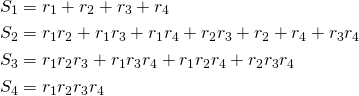
It is now easy to see, by induction that, for a polynomial of degree n: 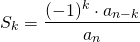 , where
, where 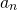 is the leading coefficient.
is the leading coefficient.
Sources: