[1]
0 and 1 is enough but not practical enough
1. What is Sorting?
Sorting, in mathematical sense, is nothing but process of arranging items in a sequence ordered by some criterion. In many cases, items are real numbers and criterion asks us to rearrange them in non decreasing order. For example, given sequence of 10 real numbers
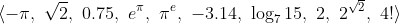
(sorry if the numbers are confusing :] ) the correct sorted output of this sequence would be
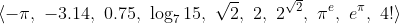
In order to sort given sequences, we must perform repeated comparisons between two chosen numbers. These are called comparison sorting.
There are indeed sorting techniques which do not accompany comparisons between numbers, but these algorithms require further restrictions on the input, such as set of integers or evenly distributed over a closed interval something like that. Since we are dealing with inputs with no restrictions on the real line, we must use comparison sorts.
2. Modeling the Process of Sorting
Now, any comparison sorting can be represented using the following diagram.
In detail, it consists of three parts
Input sequence
Output sequence (which is rearrangement in non decreasing order)
A network that actually performs comparisons and rearrangements.
The important part is the network 
. How do we specify the structure of ? It should contain all the information about comparisons we've done. For simplicity, let's look at the simplest network, which rearranges two numbers.
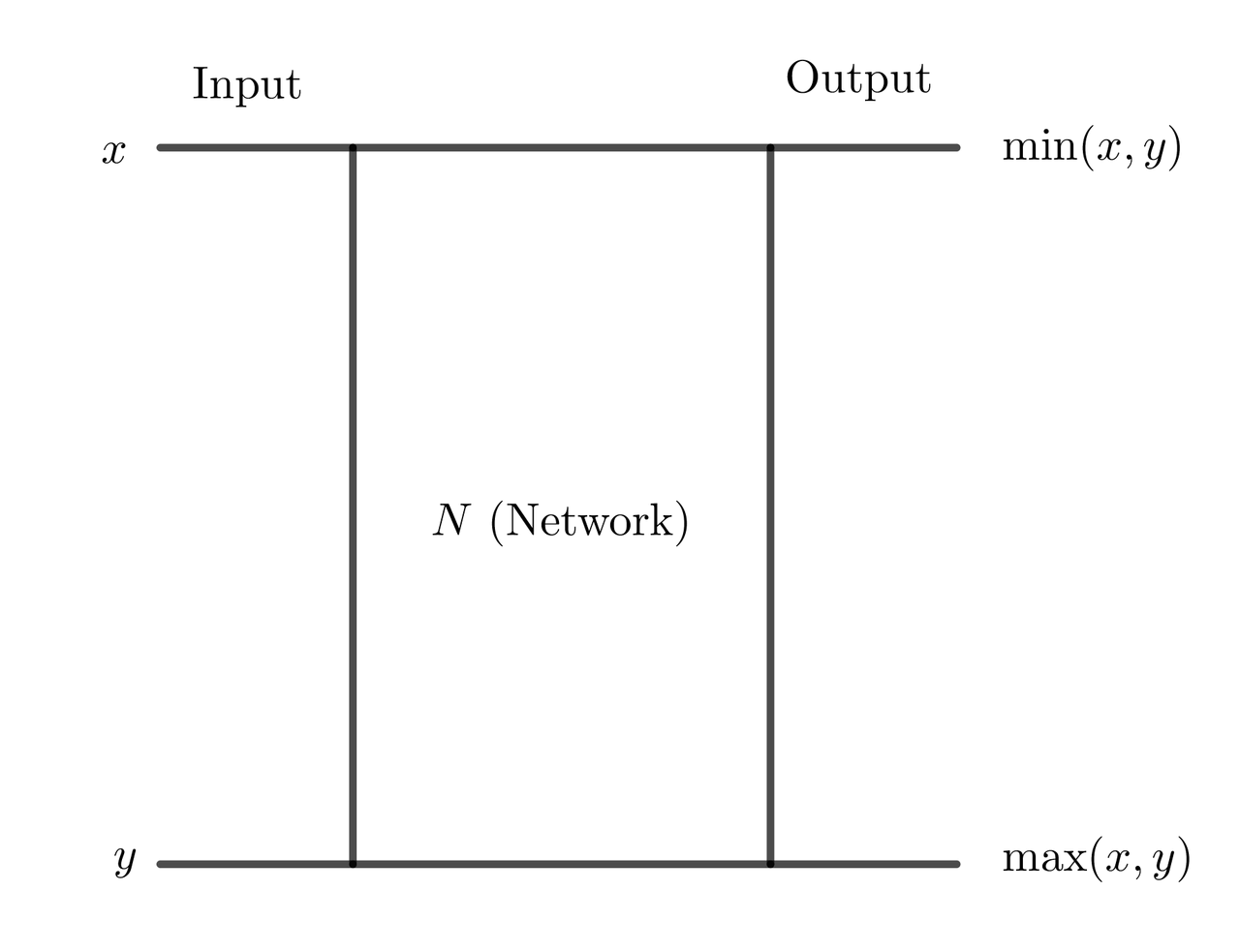
The simplest network produces minimum and maximum of two numbers. This can be modeled as a controller which sends smaller number to the top, and the other one to the bottom. So we define the fundamental network, called comparator , as follows.
For input sequence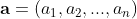 
and given integer 
, comparator is a function 
such that
So a comparator is just a network of comparing two numbers 
, leaving others unchanged. - [2]
Since sorting is just simultaneous application of comparators, an arbitrary sorting network is modeled as follows.
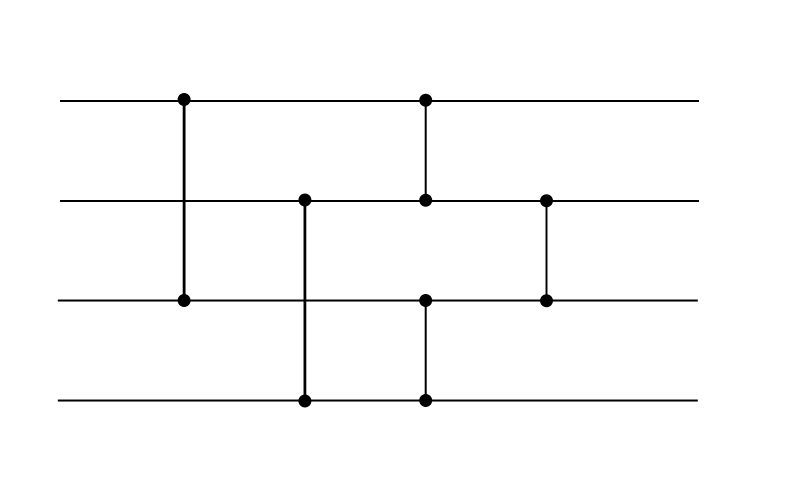
[3]
where each vertical line segements represent comparators. For example, in the following sorting network you can see that simultaneous application of 5 comparators gives sorted output <1,2,3,4>.
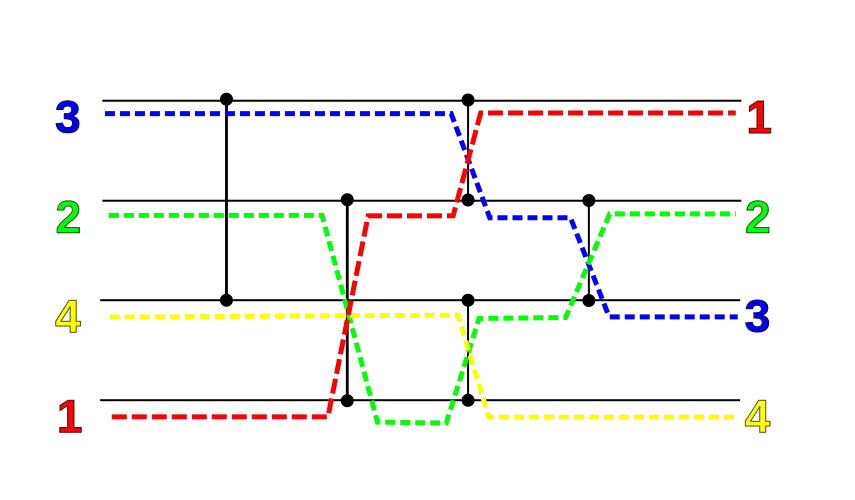
[4]
3. All Possible Inputs?
Suppose we are given a sorting network 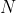, without any information about 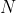itself. That is, we do not know the structure of 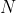; position of each comparators as well as algorithm behind it. And here comes the question.
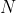? Since we do not know the structure, what we can do is just comparing input - output relationships produced by .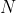
The total number of orderings such that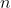 
length sequence can have is 
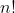, so it is impossible to investigate every input-output relationships if 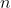gets large. Our real question is then,
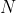is correct ? The answer is... YES! and this is called 0-1 sorting principle.
4. 0-1 Sorting principle
Now we state the 0-1 sorting principle. - [5]
0-1 Sorting Principle.
If a sorting network sorts every sequence of 0's and 1's (that is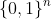 
) , then it sorts every other arbitrary sequence of length .
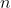So only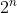 
number of testing is enough. To prove this we need two ingredients. For any 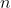length sequence 
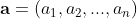, we define
A non-decreasing function 
on domain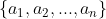 
and
Multi-valued function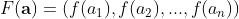 
.
Using definition of comparator, we have
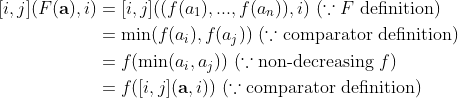
Using function diagram,
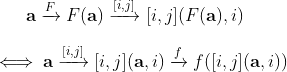
The meaning of this diagram is simple, that
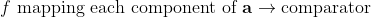
is equal to
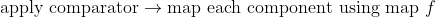
commutative . For an arbitrary sorting network 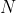(which is a composition of comparators) and a monotonic mapping 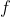we have therefore
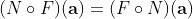
Hardest Part -[5]
Now let 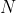be a sorting network such that sorts all sequence of 0's and 1's correctly, but there exists an input - output relationship 
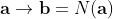which the output is not sorted. Then there is an integer 
such that
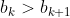
The clever trick is to construct a following non-decreasing function 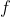such that
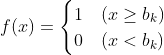
Surely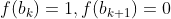 
. So
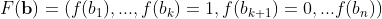
is unsorted sequence. Using commutative relationship,
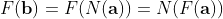
and since we assumed that 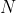sorts 0-1 sequence correctly, we get the contradiction because 
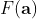is by definition, a 0-1 sequence.
5. Application ? - Hmm...
So in the case of unknown sorting network (or algorithm), 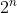number of all 0-1 sequences give the answer for correctness. But is 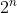small enough to be tested? Well,
It is definitely smaller than
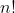for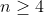 
, (in fact, 
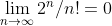)but
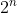itself is also exponential!
Try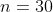 
. If you want to test the correctness of algorithm that sorts length 30 sequence, you should investigate 1,073,741,824 in-out relationships, which exceeds 1 billion ...
Surely it is correct but not practical for real world applications... Also, the sad fact is that 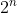is actually tight bound for testing the correctness. Testing less than 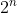does not guarantee the correctness. (This is easy you can verify by yourself).
6. Conclusion
0-1 is enough but not practical enough.
7. Citations
[2] http://www.iti.fh-flensburg.de/lang/algorithmen/sortieren/networks/sortieren.htm (definition citation)
[5] D.E. Knuth: The Art of Computer Programming, Vol. 3 - Sorting and Searching. Addison-Wesley (1973)