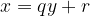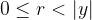(Image Source Link, CC0 license)
We all know how to obtain quotients and remainder using the division algorithm for integers. But why is it always possible to have a unique pair of quotient and remainder? This stems from the well ordering principle.
Well Ordering Principle
The precise proof of existence and uniqueness of quotient and remainder in the division algorithm heavily relies on well ordering principle. Well ordering principle comes from axiomatic set theory, so to make long story short, it states that any non-empty subset of natural numbers (= non-negative integers) contains a least element.
Well Ordering Principle. Every nonempty subset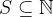 
contains an integer 
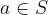such that 
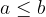for all 
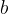's belonging to 
.
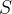In fact, there are several ways to construct Natural numbers. If you follow Peano arithmetic, then Well ordering principle is a direct consequence of principle of mathematical induction. On the other hand, if you follow axiomatic set theory; natural numbers are the smallest inductive set, then well ordering principle becomes trivial by construction itself. In either case, it is a fundamental fact, so do not try to find counterexamples...
Well known Division algorithm
The integer division algorithm can be summarized as follows.
Integer Division Algorithm. Given two integers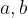 
, with 
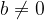, there exist unique integers 
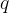and 
satisfying
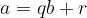with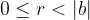
We call
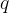as the quotient, as the remainder.
For example, for two integers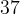 
and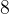 
, we have relation
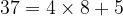
so that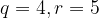 
. Another example involving negative integers would be 
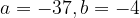, then the relation becomes
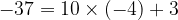
so that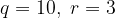 
. We can clearly see that in integer division algorithm, quotient and remainder is unique.
Why do they exist?
Well ordering principle can give us a lot of help in proving existence. For given two integers 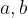with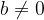 
, construct a subset of natural numbers
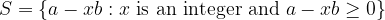
In order to use well ordering principle, we must show that 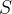is nonempty. If 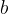is positive, we need some negative integer 
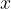satisfying 
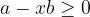. A good guess would be 
. In fact,
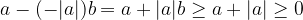
makes nonempty. Also, if is negative, 
will give us a desired result. Either case S is nonempty, so the set 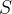contains a smllest element, namely using well ordering principle. By definition of 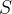, there exist an integer 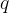such that
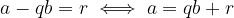
Are we done? Not yet. We must show that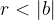 
. Here we use the method of contradiction assuming 
.
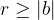Assume
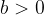. Then 
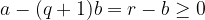so that 
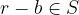. However, this contradicts to the choice of as the smallest element of 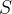.Assume
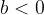. Then
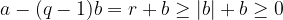
so that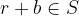 
. Again this leads to contradiction. Thus .
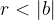Why are they unique?
Technically, showing uniqueness is easy. Suppose there are two different pairs of quotient and remiander.
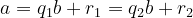
. Then
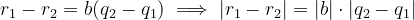
Since both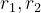 
satisfy 
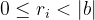, the difference should be less than 
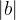. Therefore, 
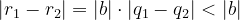leads to
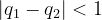
Because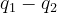 
is an integer, the only possibility is 
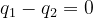, whence 
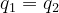. From this, we get 
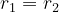, ending the proof of uniqueness.
Extension to any real number
The division algorithm of integers can be easily extended to division involving two real numbers. For two real numbers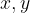 
with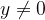 
, there always exist a quotient 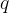and remainder such that
Note that quotient is an integer but remainder isn't.
If we fix a nonzero real number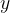 
as 1, then we can partition the set of real numbers by equivalence classes
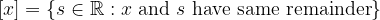
This is equivalent to saying that any equivalence class has 1-1 correspondance with unit interval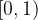 
by
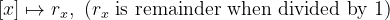
If you are familiar with quotient groups, what we've constructed is a quotient group
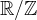
. With a continuous function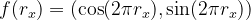 
defined on unit interval [0, 1), this group can be viewed as a unit circle on a 2D plane.
Conclusion
Well Ordering principle helps us to prove the existence of quotient and remainder in integer division algorithm.
In fact, quotient and remainder are unique.
We can extend this division algorithm to real numbers. Furthermore, each equivalence class of remainder corresponds to unique point in unit interval [0, 1).
This can be viewed as another way of representing unit circle.
Notable sources
- Elementary number theory - David M.Burton Chapter 2, Section 1.
