Contribution to the development of Mathematics by The Pythagoreans

Continuing from Thales, we will discuss the contribution of Pythagoras and The Pythagoreans into the development of Mahthematics as we know it toay.
Pythagoras is named as one of the great mathematicians ever existed. His name is used for the relationship among sides of a Right Angled Triangle as “Pythagorean Theorem”. But Pythagoras’s contribution to mathematics and philosophy is way more than just this theorem. We still use his name after about 2600 years.
Very little is known about his life. Pythagoras was born in Samos in 580BC on the western coast of what is now Turkey. He met Thales, likely as a young man and he traveled to Egypt with him. It seems certain that he gained much of his knowledge from the Egyptians, as had Thales before him. He had a reputation of having a wide range of knowledge over many subjects, though to one author as having little wisdom (Heraclitus) and to another as profoundly wise (Empedocles).
There is almost no evidence exists to prove Pythagoras’s own individual achievements but he was referred by late historians and mathematicians in their writings. Neither Pythagoras himself nor his immediate successors left any doctrine or solid proof of their achievements. The knowledge about the Pythagoras and Pythagoreans comes from others, including Aristotle, Theon of Smyrna, Plato, Herodotus, Philolaus of Tarentum, and others. It is believed that The Pythagorean philosophy was the prime source of inspiration for Plato and Aristotle.
It is very certain that the Theory of Numbers was developed in the school of Pythagoreans with the personal involvement of Pythagoras.
Achievements:
- Pythagoreans considered the number “1” just not a number itself but the beginning. The dictum of the Pythagorean School was “All is Number” According to Aristotle’s Metaphysics “The Pythagoreans expended great effort to form the numbers from a single number, the Unit, (i.e. one). They treated the unit, which is a point without position, as a point, and a point as a unit having position. The unit was not originally considered a number, because a measure is not the things measured, but the measure of the One is the beginning of number.” (I wonder it is very much same as explained in EKK OUNG KAAR, the meaning of EKK). For Pythagoreans the numbers are not mere numbers but they attached the numbers to qualities and attributes.
- Recognize the even and odd numbers.
- It is found in Aristotle’s writings that The Pythagoreans assume One as both even and odd.
- Classification of numbers based on prime and composite numbers
- Perfect number; a number which is equal to sum of its parts (factors excluding itself but including 1); is called the perfect number; for example 6; 6 = 1 + 2 + 3 .The other examples of perfect numbers are 28 and 496.
- Discovered friendly numbers
- Discovered musical intervals such as 4:3 (the fourth), 3:2 (the fifth) and 2:1 (the octave), proved that musical notes could be translated into mathematical equations.
- Pythagorean observed that 10 contains in it the “Point”, “Linear”, “Plane” and “Solid” varieties of a number. 1 is a point, 2 is a line, 3 is plane and 4 is solid.
- Figured Numbers: It seems to go back to Pythagoras himself. A dot is a point which represents 1, two dots represent 2 and once joined define a straight line. Similarly 3 dots in the same plane represent the triangle which is first rectilinear plane figure. Four dots 3 in the same plane and fourth outside the plane represent a solid.
- Discovered that the sum of any number of successive terms of the series of natural numbers (1, 2, 3, 4, 5………..) beginning from 1 makes a triangular number.
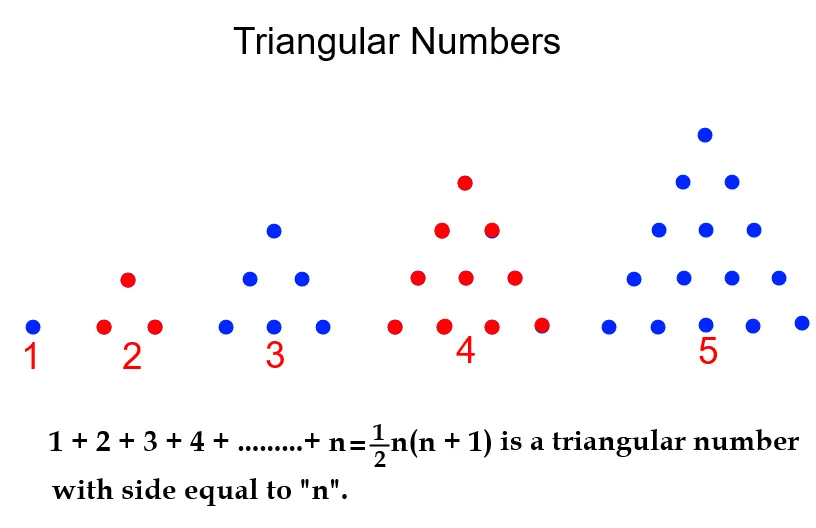
- Discovered the square numbers. If we have a number of dot(s) forming and filling up a square then we can get the next higher square by adding two rows of dots round the two adjacent sides of the original square. I explained it below; 1 + 3 = 4, Added “first two” odd numbers gives the square of “2”. 1 + 3 + 5 = 9, Added “first three” odd numbers generates the square of “3”
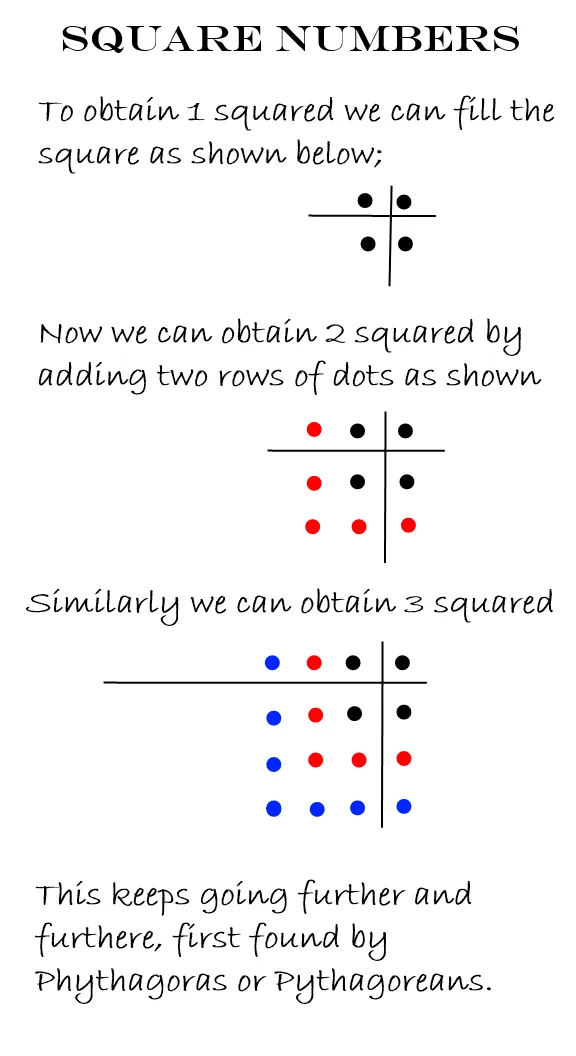

You see, how the sum of these successive odd numbers makes the perfect squares.
- GNOMONS: The odd numbers successively added are known as gnomons. Originally the gnomon was an astronomical instrument used to measure time. Gnomon was also used for a square edge to draw right angles.
- Developed theory of means and proportions.
- Sum of three angles of a triangle is equal to two right angles.
- Discovery of The Theory of Irrationals according to Proclus.
- Pythagorean triplets and Pythagorean Theorem.

- Many other discoveries of theorems involving triangles, circles, parallel lines and polygons are discovered by Pythagoreans.
If you want to study about the Pythagoras and The School of Pythagorean then you can download the following pdf booklet;