Image source: http://www.soulphysics.org
In my previous post, I introduced some basic concepts in combinatorics. If you haven't read the previous post, you can do so here.
Arranging objects when some objects are identical
A common question "ball-picking" question asked in the early rounds of math competitions might sound something like this:
Bob has a set of 12 colored balls. Three of the balls are red, seven are blue, and six are green. In how many distinct ways can he arrange the balls?
If all the balls had a distinct color, then the number of possible ways to arrange the balls is obviously an astonishing 12!, or 479001600 different ways. If all the balls are of the same color, then it doesn't matter how we arrange them; the lineup will look the same no matter what. Obviously, in this case, the "type" of object (in this case, distinguished by color) also matters.
Suppose for a moment that the three red balls are placed in positions 2, 8, and 9. It doesn't matter which identical red ball is in which position, so this effectively means we divide by 3!. If we follow through with the other colors we would obtain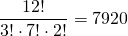 
ways of arranging these 12 balls.
In general, given a set of size N which contains subsets of sizes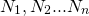 
, with each subset containing identical items, the number of possible arrangements is: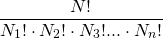 
Picking objects with replacement
Suppose now, instead of picking k objects from a set of n, that some of the objects can be replaced. In other words, we can now choose an element more than once. It should be fairly obvious that, if the order isn't important, we would have simply
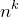possibilities. The most straightforward example of this is the number of possible n-digit, non-negative integers. There are 10 possibilities for each place value, and thus there are 
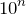possibilities.
In the case that the order does not matter, things will be slightly different. In this case, multiplicity is explicitly significant, as we are now allowed to choose a set such as {1, 1, 3, 4}. At the same time, {1, 1, 3, 4} is equivalent to {4, 1, 3, 1}. In this case, the number of possible ways to choose is: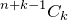 
. Multichoose problems are sometimes called "bars and stars" problems; you can read more about this problem here.
Paths between lattice points
We'll conclude our discussion with an interesting question that has appeared in many forms over the year:
Suppose we have a small city with m+1 streets running north to south and n + 1 streets running east to west. How many ways can we drive from the Southwest corner of the city to the northeast, if we can only travel in the north or east directions?
Another way of asking this question is At first, this will seem a bit daunting, but it is not terribly difficult when using what we've just learned.
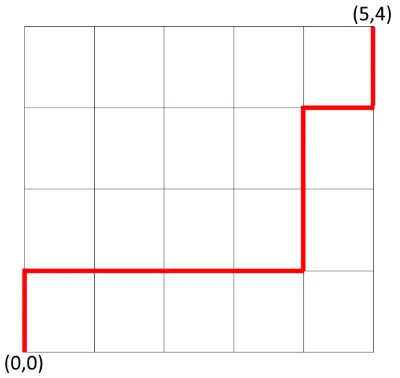
One possible path through the city
Let's assume that the southwest corner of the town is located at position (0,0), which means that the northeast corner is located at (m, n). Furthermore, we can say that driving one block to the east as "E" and one block to the north as "N". For example, if m = 5 and n = 4, we could get from the starting point to the destination by driving five blocks to the east and four blocks to the north, or EEEEENNNN. Every path must therefore go east m times and to the north n times. In total there must, and in total there are m + n steps.
From here, we only need to choose which of the m steps involve travelling east. This gives us a final answer of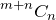 
possible paths.