
Every year, MIT hosts an "integration bee" in which first-year students compete to solve increasingly complex integrals using techniques they've learned in calculus. MIT's first integration bee was held in 1981, and has drawn large crowds ever since [1]. The competition usually consists of a qualifying round and a final round. Here is one of the questions from the qualifying round: (source)
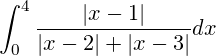
If you make it to the final round, you'll find that many of these integrals are far beyond the routine textbook exercises that most students will encounter, and require a bit of ingenuity, skill, and creativity to solve. The concepts needed aren't typically beyond those of a first year calculus course, but the idea is to find the "trick" behind them. Here is one such question from 2015 competition. Can you solve it?
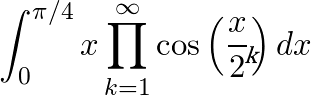
The entirety of the 2015 Integration Bee Final can be viewed here.
If you think you know, make a comment below. Don't cheat and watch the answer in the video!
Hint 1: Double angle formulas
Hint 2: L'Hopital's Rule