Combinatorics
”the branch of mathematics dealing with combinations of objects belonging to a finite set in accordance with certain constraints, such as those of graph theory.” – Google Definition

I loved this class. It makes things in probability so much easier! Here are a few great examples!
One
How many possible scantrons can a teacher receive if he has a test with 10 true/false questions?
Think of it this way… You have ten spots
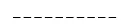
Each spot can have 2 possible answers, so we have
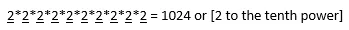
So, for fun, what is the probability that a student can guess all of the right answers? Well,
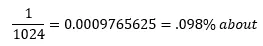
Not a chance. This is the reason why I am comfortable using T/F as a teacher. Haha.
Two
If there are 15 people in a race where the top 3 spots move on to the next race. How many possible orders can there be for the racers?
There are two ways to think about this…
A) Combinatorics: Use the same placement system we used in the last problem… 15 people can be first, 14 people can be second, and 13 people can be third. So,
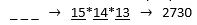
B) Probability: Since order matters and we are choosing 3 we can use a permutation [Remember that a combination is unordered]. The math looks like this:

