Computer Science education teaches "Big O" notation for describing complexity upper bounds, and Big-Theta and Big-Omega get introduced as well. Mathematicians and complexity theorists sometimes use "little o" as a stronger description of asymptotic behavior. But here are some bounds you may not have learned.
Big-D notation
f(x) is D(g(x)) if you plot the two on Desmos, and it looks like f(x) < g(x).
Example: n^r is D( log(n) ) for small values of r, even though log(n) is O(n^r)for any positive r.
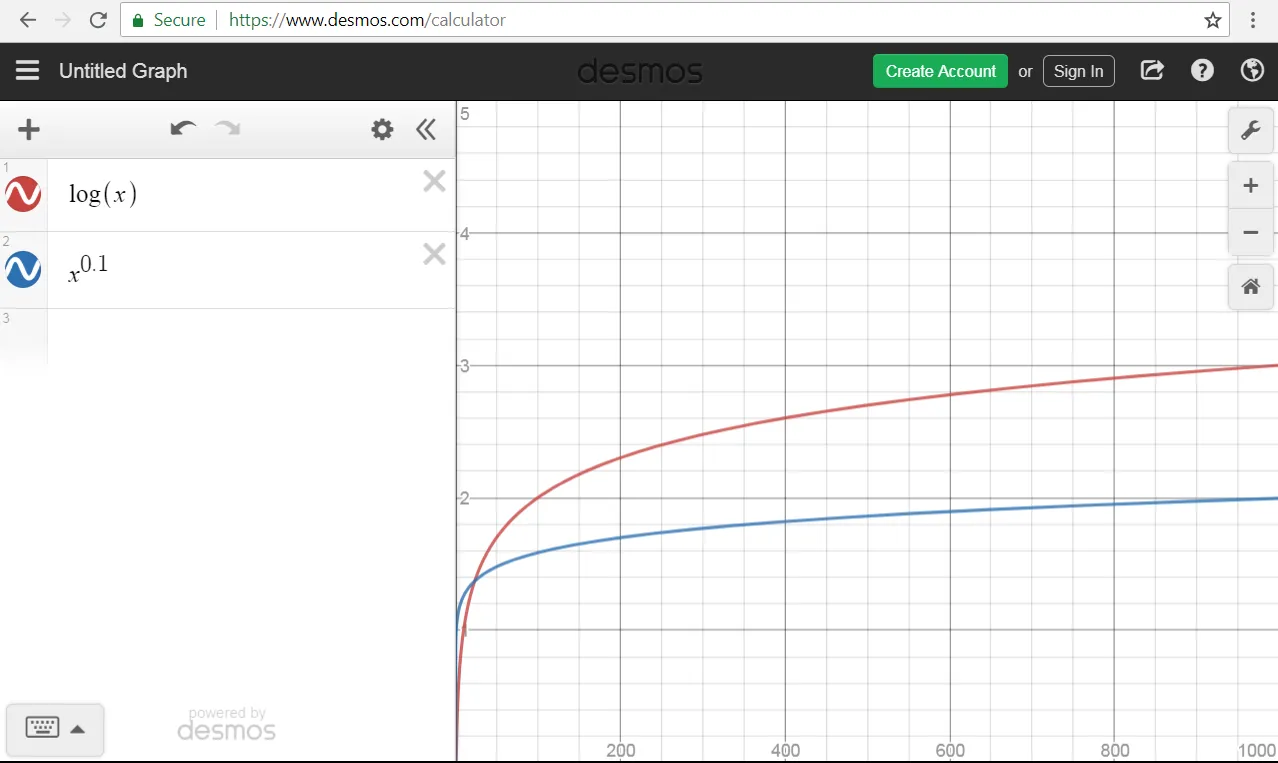
This notation is surprisingly popular with many students, perhaps due to trouble distinguishing a handwritten 'O' from a handwritten 'D'. Unfortunately, the broader mathematical community is resistant to this innovation in asymptotic analysis.
little-w asymptotic bound
f(x) is w(g(x)) if you hand-wave hard enough that the two are equivalent.
Example: 2^(n/2) is w(2^n), because all running times that use an exponent are the same.
This notation frequently gets used in the context of NP-complete problems where it asserted that the best known running time is w(2^n). (Upper bounds on 3SAT are actually as low as O(1.321^n) for a randomized algorithm.)
curly-O notation
The curly-O notation is the same as big-O, but reserved for those who want to show off their typesetting or calligraphy skills.
Example:

QWT-boundedness
A decision function that could be computed in time f(n) on a quantum computer because it "explores all universes simultaneously" is QWT(f(n))
(Editor's note: that's not how quantum computers work.)
Πnotation
A randomized procedure's run time is Œ( g(x) ) if the bound on its expected run time is O(g(x)), or if the function is described in Old English.
Example: lookup in a hash table takes Œ(1) time. It does not take O(1) time as sloppy writing sometimes indicates.
Example: the notorious Beowulf reduction demonstrates the complexity class M_onsters are all Œ(Geats). "Hwæt. We Gardena in geardagum, þeodcyninga, þrym gefrunon, hu ða æþelingas ellen fremedon...."
Shrug relation
f(x) ¯\_(ツ)_/¯ g(x) if either f(x) is asymptotically less than g(x), or g(x) is asymptotically less than f(x), but we're not sure which, or the proof is too complicated to explain.
Example: The Slow-growing hierarchy g_α(n) eventually catches up with the Fast-growing hierarchy f_α(n), so f_α(n) ¯\_(ツ)_/¯ g_α(n) because who understands infinite ordinals anyway.