In my earlier videos I went over a useful strategy for integration but with that a very important question arises: can we use our integration strategy to integrate all continuous functions? The answer to that question is unfortunately NO, well at least not in terms of the regular elementary functions. In this video I go over what elementary functions are and explain how most elementary functions, such as ex2 can not be integrated in terms of basic elementary functions. One method to prove whether or not a function can be integrated in terms of elementary functions is called the Risch Algorithm and was developed in 1968 by the American Mathematician Robert Henry Risch.
In my later videos I will go over how functions such as ex2 can be integrated in terms of infinite series so stay tuned for that!
Watch Video On:
Download Video Notes: https://1drv.ms/b/s!As32ynv0LoaIhd4iIg7HrqROZAvF2w
View Video Notes Below!
Download These Notes: Link is in Video Description.
View These Notes as an Article: https://steemit.com/@mes
Subscribe via Email: http://mes.fm/subscribe
Donate! :) https://mes.fm/donateReuse of My Videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight Back Against Censorship:
- Bookmark sites/channels/accounts and check periodically
- Remember to always archive website pages in case they get deleted/changed.
Join my private Discord Chat Room: https://mes.fm/chatroom
Check out my Reddit and Voat Math Forums:
Buy "Where Did The Towers Go?" by Dr. Judy Wood: https://mes.fm/judywoodbook
Follow My #FreeEnergy Video Series: https://mes.fm/freeenergy-playlist
Watch my #AntiGravity Video Series: https://steemit.com/antigravity/@mes/series
- See Part 6 for my Self Appointed PhD and #MESDuality Breakthrough Concept!
Follow My #MESExperiments Video Series: https://steemit.com/mesexperiments/@mes/list
NOTE #1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (If Available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed. (#Try2xSpeed)
-- Try 4X+ Speed by Browser Extensions or Modifying Source Code.
-- Browser Extension Recommendation: https://mes.fm/videospeed-extension
-- See my tutorial to learn more: https://steemit.com/video/@mes/play-videos-at-faster-or-slower-speeds-on-any-website- Download and Read Notes.
- Read notes on Steemit #GetOnSteem
- Watch the video in parts.
NOTE #2: If video volume is too low at any part of the video:
- Download this Browser Extension Recommendation: https://mes.fm/volume-extension
Strategy for Integration: Can we Integrate All Continuous Functions?

The question arises: Will our strategy for integration enable us to find the integral of every continuous functions?
For example, can we use it to evaluate the integral:
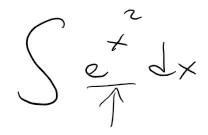
The answer is no, well at least not in terms of the functions we are familiar with.
The functions that I have covered so far in my videos are called elementary functions.
These are the polynomials, rational functions, power functions (xn), exponential functions (ax), trigonometric and inverse trigonometric functions, hyperbolic and inverse hyperbolic functions, and all functions that can be obtained from these by the five operations of addition, subtraction, multiplication, division, and composition.
For example the following function is an elementary function:
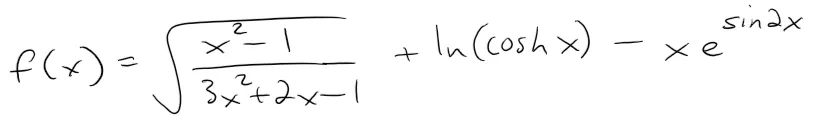
If f is an elementary function, then f' is an elementary function BUT ∫f(x)dx doesn't necessarily have to be an elementary function.
Consider the function:

Since the function is continuous, its integral exists and if we define the function F by:
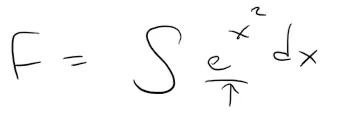
Then we know by part 1 of the Fundamental Theorem of Calculus that:
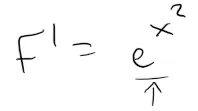
Thus, the function f has an antiderivative F, but it has been proved that F is not an elementary function.
- Whether a function is elementary or not can be proven by the Risch Alogrithm
- Named after the American Mathematician Robert Henry Risch who developed the algorithm in 1968 and called it the Decision Procedure since it is a method for deciding whether a function has an elementary function as an indefinite integral, and if it does, determining it.
This means that no matter how hard we try, we will never succeed in evaluating F in terms of functions we know.
- In my later videos however, I will show how to express F as an infinite series.
The same can be said for the following integrals as well:

In fact, the majority of elementary functions don’t have elementary antiderivatives!
