▶️Watch on 3Speak - Odysee - BitChute - Rumble - YouTube - PDF notes
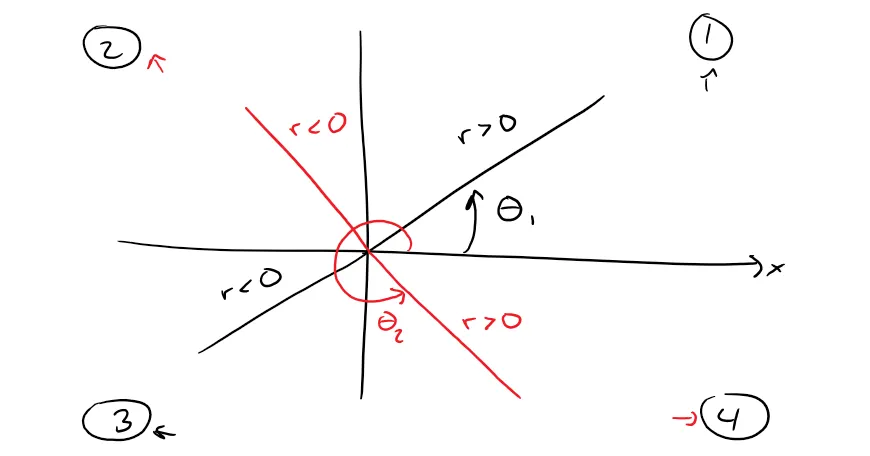
In this video I go over another example on polar coordinates and this time look at how to make straight line segments that pass through the origin. The example I look at is graphing the straight line segment formed by the polar equation θ = 1 radian. This means that for every distance from the origin r, the angle remains the same which is θ = 1 radian. Thus we get a straight line with a consistent angle. The polar coordinate system shows how it is very easy to formulate straight line segments that pass through the origin, again because of the circular nature of its definition. This is a quick video to illustrate the polar coordinate system in graphing straight lines, so make sure to watch it!
Polar Coordinates Playlist
View Video Notes Below!
Become a MES Super Fan - Donate - Subscribe via email - MES merchandise
Reuse of my videos:
- Feel free to make use of / re-upload / monetize my videos as long as you provide a link to the original video.
Fight back against censorship:
- Bookmark sites/channels/accounts and check periodically.
- Remember to always archive website pages in case they get deleted/changed.
Recommended Books: "Where Did the Towers Go?" by Dr. Judy Wood
Join my forums: Hive community - Reddit - Discord
Follow along my epic video series: MES Science - MES Experiments - Anti-Gravity (MES Duality) - Free Energy - PG
NOTE 1: If you don't have time to watch this whole video:
- Skip to the end for Summary and Conclusions (if available)
- Play this video at a faster speed.
-- TOP SECRET LIFE HACK: Your brain gets used to faster speed!
-- MES tutorial- Download and read video notes.
- Read notes on the Hive blockchain $HIVE
- Watch the video in parts.
-- Timestamps of all parts are in the description.Browser extension recommendations: Increase video speed - Increase video audio - Text to speech (Android app) – Archive webpages
Example: Sketch the polar curve θ = 1
This curve consists of all points (r , θ) such that the polar angle θ is 1 radian.
It is thus a straight line that passes through the origin O and makes an angle of 1 radian with the polar axis, as shown below:
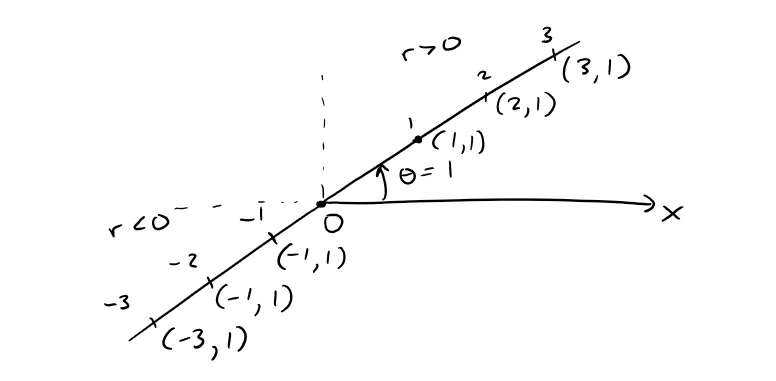
Notice that the points (r , 1) on the line with r > 0 are in the first quadrant, whereas those with r < 0 are in the third quadrant (i.e. the opposite quadrant).