Have you ever thought about why we count to 10 instead of 8, 9, 11 or better still 12? The decimal counting system (or base 10) feels intuitive and logical, but is there something better out there?

You bet there is! Base 12 could do a much better job for us in our everyday lives. Let's see why!

Why Do We Use The Decimal Numeral System?

The decimal numeral system is the counting system we are the most familiar with because we use it every day. It uses 10 digits (from 0 to 9) and the position of each digit in a particular number represents a different power of ten. The larger the number, the more digits we use to express it.

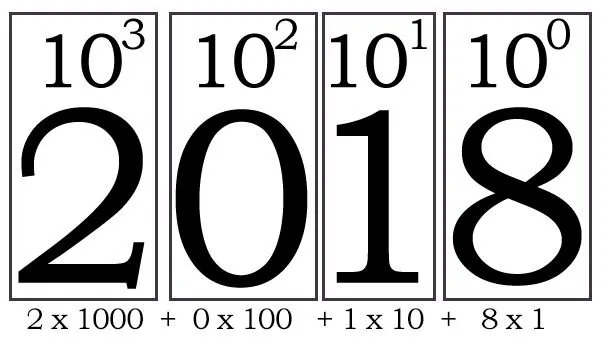
For instance we can look at the current year - 2018 - and notice what each digit represents. We have different digits representing the ones (10⁰), tens (10¹), hundreds (10²) and thousands (10³). Summing up those powers of ten gives us the number we want to represent. As we all know well from experience, it's easy to represent any number using this system.

But what is so special about ten and why do we count in tens. There are two very simple prongs to this answer.

First of all, we have ten fingers which gives us a clear reference point when counting. This makes us feel more attached to the number 10, so it feels especially round. If we had 4 fingers on each hand, could be counting in chunks of 8 instead of chunks of 10. So the first prong of the answer is sheer evolutionary chance.

The second reason we are using the decimal system is because we are used to it. It's part of our most languages and this is how we are introduced to numbers as children. For pretty much all of us, this system is carved into the way we think about math and numbers and nothing feels more natural. On top of this, everything around us is based on that system and we see it so much that we don't even think about alternatives. This is how entrenched into our lives the decimal system actually is.

But as mentioned above, the fact that random chance and habit are pointing towards a particular solution doesn't mean that this is the optimal solution. And indeed, in a perfect world, we would be able to switch to something superior...

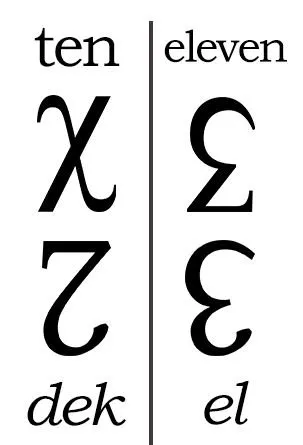
Say Hello to Base 12

Base 12, also known as dozenal or duodecimal, is an alternative numeral system that uses 12 digits instead of 10 and where the position of each digit represents a power of 12 instead of a power of 10. But to start looking at it, we are going to need two more digits to represent ten and eleven. There are different options like using X to represent 10 and E to represent 11 or new symbols like the ones on the right. To avoid confusion, we not only need new digits, but we also need new words for ten, eleven and twelve which are respectively dek, el and do (coming from dozen).

When using this system we can use the twelve digits (from 0 to 9 plus the two new ones) to create numbers in the same way that we used in decimal. The only real difference is that each position would represent a power of 12 instead of a power of 10. This means that we will have 12⁰, 12¹, 12², 12³ and so on. Iinstead of having round numbers that divide by 10, the round numbers in duodecimal will divide by 12.

We can take a look at the numbers from 1 to 24 written in base 12 below with a few corresponding numbers from base 10 written in red for reference.

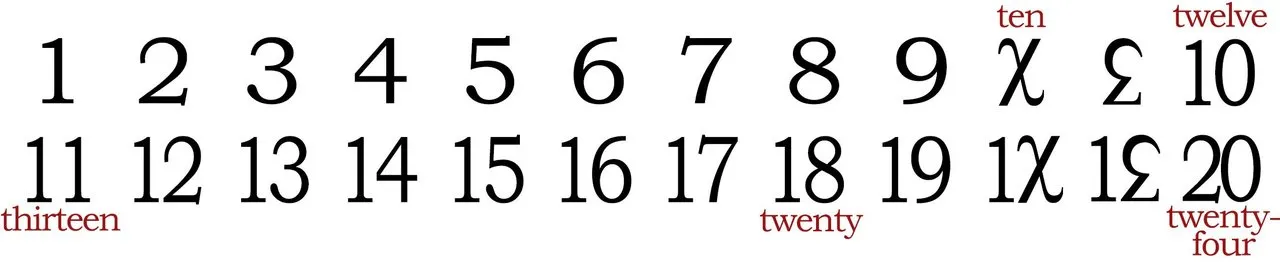
Just like in base 10, we can continue making larger and larger numbers. When we write 10 in base 12, it stands for 12¹ or 12. When we write 100 in base 12, it stands for 12² or 144 which is also called gross or gro. When we write 1000 in base 12, it stands for 12³ or 1728 which is also called mo and so on. The number expressed as 20 in base 12 (or 24 in base 10) would be pronounced two-do and the number expressed as 200 in base 12 (or 288 in base 10) would be pronounced two-gro.

To get another example of a number written in base 12, we can look at our current year. It might be 2018 in decimal, but it's 1202 in duodecimal:

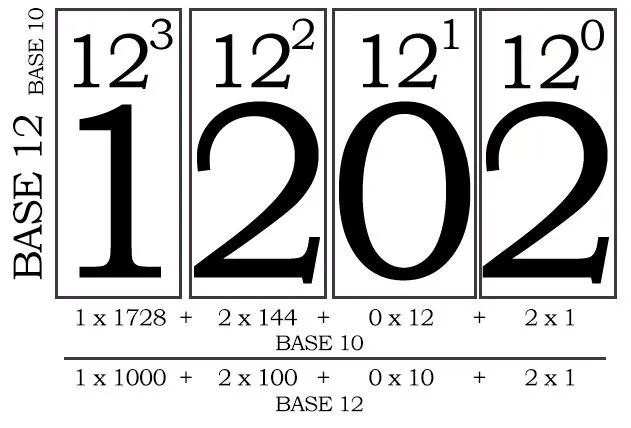
It might not be very easy to get used to in the begining, but it's actually very similar to the way things work in decimal.

But What Makes Duodecimal Better?

To put in simply, once you get used to it, everyday math would be much easier in duodecimal.

1. Fractions Are Easier

You see, ten has only two factors besides itself and one - 2 and 5. Twelve on the other hand, has more - 2, 3, 4 and 6. This means that counting in twelves gives us the advantage of being able to divide things in more ways more easily. Having more factors makes base 12 much more flexible. The grids below show the important fractions that are easy to do in each system in a way that's hopefully easier to imagine.

$fractions400.jpg$

A grid of 12 parts is easy to divide into a half, a third and a quarter while a grid of 10 parts is easy to divide only in half. This means that fractions in base 12 are going to be much easier to handle.

To demonstrate this we can use another real-live example. If we have a pre-cut pizza to divide among groups of people of different sizes, cutting the pizza in 12 slices will give us a lot more options to divide it.

We can see that for groups between 2 and 6, a pizza divided in 12 slices gives us a lot more options than a pizza divided in 10 slices.

Well, this works out for other fractions too. Having more factors means that working with fractions is going to be much easier in duodecimal. While ⅓ in base 10 is a problem as it's 0.3333333 with an infinitely recurring series of 3s, ⅓ in duodecimal would be 0.4 as it's 4/12. While ¼ in base 10 is not infinite (0.25), base 12 still offers an improvement with the simple 0.3 as it's 3/12. ½ in base 12 would be 0.6 as it's 6/12.

While there are still some fractions that would have infinitely recurring parts in base 12 like 1/5 and 1/7, using it would still offer a significant advantage over base 10 and most of the fractions we are likely to encounter in our everyday life would be simplified.

2. The Multiplication Table Is Easier

Fractions are not the only part of everyday math that will become much easier in duodecimal. In decimal, the easiest part of the multiplication table is multiplying by 5 as it gives very predictable results with a very simple recurring pattern. This happens because 5 is a factor of 10 which allows for things to line up quite nicely. The results always end in 5 or 0.

Since 12 has more factors than 10, a larger part of the duodecimal multiplication table lines up with recurring patterns that would be much easier to learn and work with. Multiplying by 3, 4, 6, 8 and 9 all result in recurring patterns and only multiplying by 5 and 7 might be a bit more challenging to learn in the beginning.

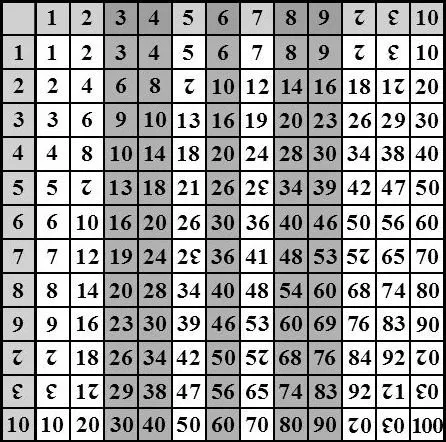
This would arguably make teaching and learning multiplication much easier. Nowadays, too many children are afraid of math and if we can make the type of math they are going to encounter early on easier, we would be less likely to scare them away from it. But having an easier multiplication table makes life easier for everybody.

An additional bonus that the duodecimal multiplication table offers is the fact that it actually covers a bit more ground before you have to switch to non-integer multiples. The decimal multiplication table reaches 100 while the duodecimal reaches 144 which means that an average person would be able to quickly calculate results for a slightly broader set of numbers after learning it.

But We Have 10 Fingers! Wouldn't Teaching Base 12 Be Too Confusing Without Using Your Fingers?

When we learn to count as children, we do indeed use our fingers, but this doesn't mean that we can't still use them in base 12. Instead of counting on our fingers, we can count on the segments of our fingers on one of our hands and viola - we get a clear visual representation of a dozen:

This also has an added bonus of clear visualizations of halfs, thirds and quarters just by looking at our hands.

It turns out that if we had been taught to count in twelves instead of in tens, both using and learning simple math would be significantly easier.

So Why Don't We Switch To Base 12 Right Away?

Unfortunately, life is never that simple. If we started learning base 12 as children, it would be easier, but switching to a new numeral system as an adult is going to be a huge pain for all of us. As mentioned in the beginning, one of the main reasons we are using decimal is that this is what we know and what we are used to. If we switched to base 12, base 10 would always feel more natural for those of use who grew up with it. And this is going to be essentially all of us.

On top of this, it's not only our heads that would need changing, it would be everything around us. Numbers are everywhere - from speed limit signs, through calculators and computer keyboards, to money. If we want to change the counting system we are using, we are going to have to change everything. We would need new calculators, we would need new computer keyboards, we would need software updates, we would need to change the dashboards on all kinds of vehicles and equipment and we would need to change virtually all signs. It's not only going to be a huge mess, but it would also cost a ton of money.

That's why, I don't think we are ever going to see duodecimal becoming the accepted way to count anytime in the foreseeable future. There would be some benefits, but the costs are simply prohibitively high. Additionally, all the benefits of base 12 can be felt in everyday math, but it doesn't really change much about the more complex math used in science or engineering. In the end, despite the fact that it's not perfect and that we have a better option, base 10 is simply good enough for us to keep using it even if we know we have a better option.

If only our fish ancestors had preserved an additional bone in their flippers for us to have 6 fingers on each hand...

Sources:

The images and illustrations in this post are all original work based on the following CC0 sources and graphics released into the public domain like the different dek and el symbols:

The Curious Case For Base 12 (Why Dozens Are Easier For Everyday Maths Than Tens)