Dominar el arte de resolver Ecuaciones Diferenciales no solo fortalece nuestras habilidades matemáticas, sino que también nos prepara para enfrentar con éxito problemas aplicados en ingeniería, física, economía y muchas otras áreas. En esta publicación te invito a explorar el método de Reducción a Ecuaciones Homogéneas, una poderosa técnica que permite transformar ciertos tipos de Ecuaciones Diferenciales en formas más manejables y resolubles.
A través de la solución detallada de 10 ejercicios tomados de diferentes Libros sobre Ecuaciones Diferenciales (ver referencias bibliográficas), aprenderás paso a paso cómo aplicar este método, identificar su estructura en problemas aparentemente distintos y desarrollar una comprensión profunda que va más allá de la simple memorización de fórmulas.
Esta es una excelente oportunidad para reforzar tus conocimientos, afinar tu pensamiento lógico y disfrutar del proceso de resolución como un verdadero desafío intelectual. ¡Vamos a descubrir juntos la belleza oculta en las Ecuaciones Diferenciales Reducibles a Homogéneas!















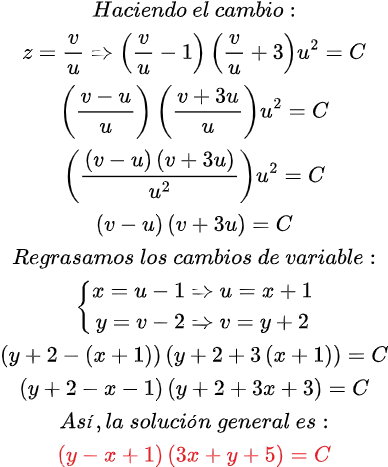
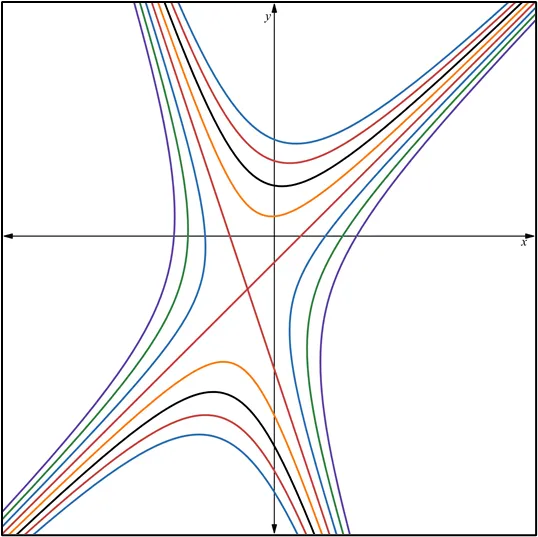
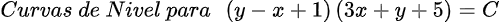


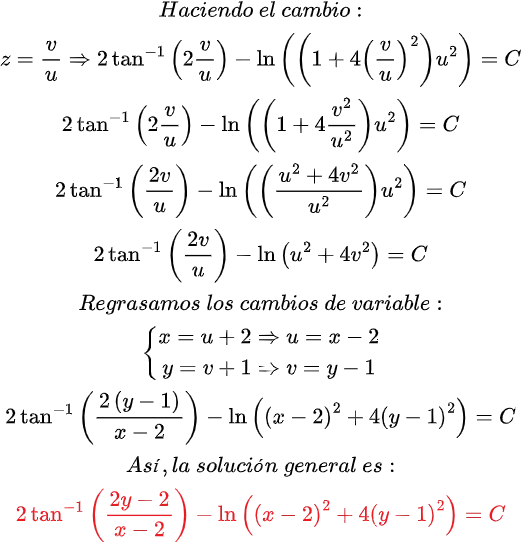

Me siento afortunado de contar con una comunidad tan entusiasta, generosa y comprometida. Sus comentarios, sugerencias y muestras de cariño han sido una fuente inagotable de motivación e inspiración para seguir creando y creciendo juntos.
Gracias por ser parte de este viaje, por su confianza y por ayudarme a mejorar cada día. Sin ustedes, nada de esto sería posible. ¡Sigamos compartiendo ideas, aprendizajes y buenos momentos en Hive Blog!.
Un fuerte abrazo,
Gary Nuñez .
DIOS LOS BENDIGA

1.- A. Kiseliov, M. Krasnov y G. Makarenko. Problemas de Ecuaciones Diferenciales Ordinarias. Editorial MIR, 1984.
2.- Acero, Ignacio. Ecuaciones Diferenciales Teoría y Problemas. Editorial Tébar, 2007.
3.- Boyce, William E., DiPrima, Richard C., Meade, Douglas B. Ecuaciones Diferenciales Elementales y Problemas de Valores en la Frontera. Editorial Wiley, 2012.
4.- C. Henry Edwards, David E. Penny. Ecuaciones Diferenciales. Editorial Pearson Educación de México, 2001.
5.- Earl D. Rainville, Phillip E. Bedient, Richard E. Bedient. Ecuaciones Diferenciales. Editorial Pearson Educación, 1997.
6.- G. Baranenkov, B. Demidovich, V. Efimenko, S. Kogany, G. Lunts, E. Porshneva, E. Sichova, S. Frolov, R. Shostak y A. Yanpolskí. Problemas y Ejercicios de Análisis Matemático. Editorial MIR, 1967.
7.- Jiménez López, Víctor. Ecuaciones Diferenciales: cómo aprenderlas, cómo enseñarlas. EDITUM, 2000.
8.- Larson, Robert P. Hostetler, Roland E. Cálculo y Geometría Analítica. Volumen 2. McGraw Hill, 1995.
9.- Morris Tenenbaum, Harry Pollard. Ecuaciones Diferenciales Ordinarias. Editorial Dover, 1963.
10.- Quintana, Pedro, Villalobos Eloísa, Cornejo María. Métodos de Solución de Ecuaciones Diferenciales y Aplicaciones. Editorial Reverte, 2008.
11.- R. Kent Nagle, Edward B. Saff, Arthur David Snider. Ecuaciones Diferenciales y Problemas con Valores en la Frontera. Editorial Pearson Educación de México, 2005.
12.- Shepley L. Ross. Ecuaciones Diferenciales. Editorial Reverté, 1992.
13.- Zill, Dennis G. Ecuaciones Diferenciales con Aplicaciones. Grupo Editorial Iberoamérica, 1988.
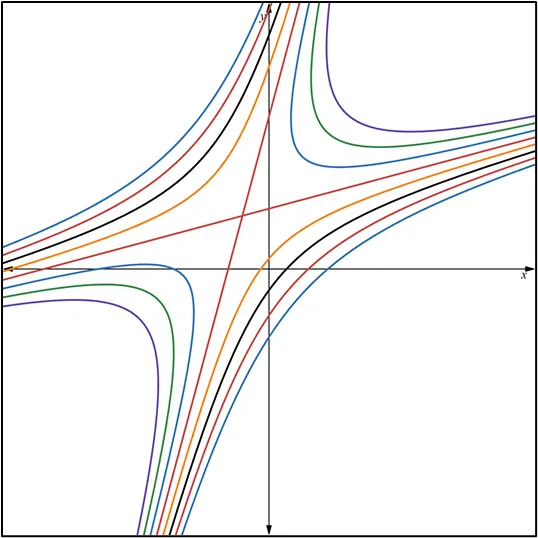
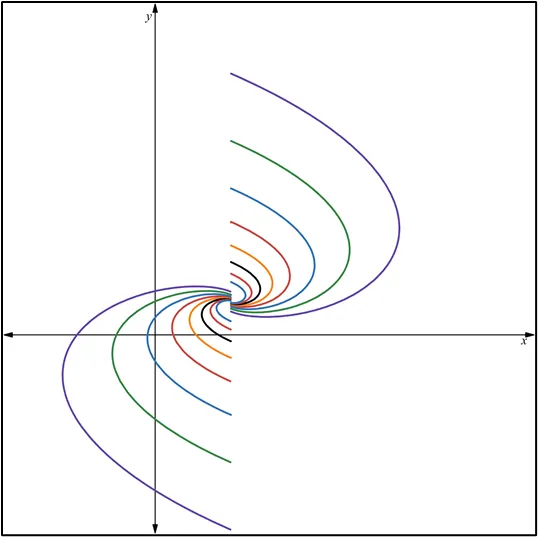
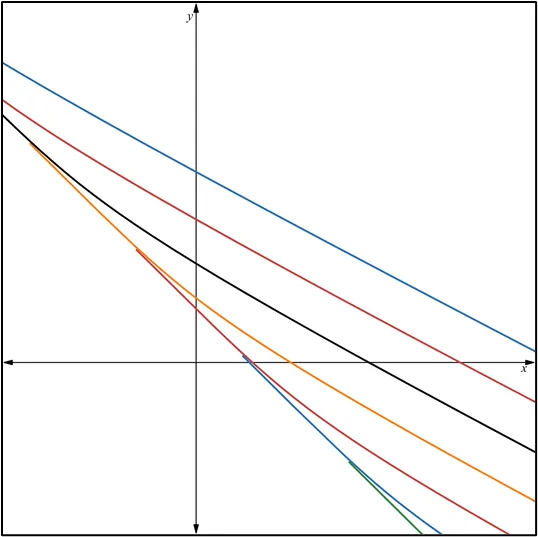
la página web: https://www.desmos.com/calculator/frx7bimvdd?lang=es.